​

一、基本概念

  机器学习：通过算法使得机器能从大量数据中学习规律从而对新的样本做决策。
  机器学习是从有限的观测数据中学习（或“猜测”）出具有一般性的规律，并可以将总结出来的规律推广应用到未观测样本上。

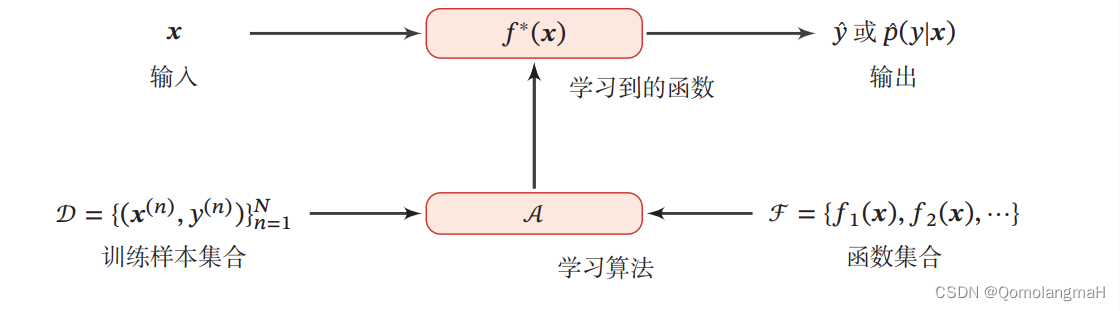
二、机器学习的三要素

  机器学习方法可以粗略地分为三个基本要素：模型、学习准则、优化算法。

1. 模型

a. 线性模型

$$f(\mathbf{x};\mathbf{\theta })={\mathbf{w}}^T\mathbf{x}+b$$

b. 非线性模型

  广义的非线性模型可以写为多个非线性基函数 $\mathbf{\varphi }(\mathbf{x})$ 的线性组合：$$f(\mathbf{x};\mathbf{\theta })={\mathbf{w}}^T\mathbf{\varphi }(\mathbf{x})+b$$其中，$\mathbf{\varphi }(\mathbf{x})=[{\varphi }_1(\mathbf{x}),{\varphi }_2(\mathbf{x}),\dots ,{\varphi }_K(\mathbf{x}){]}^T$ 是由 $K$ 个非线性基函数组成的向量，参数 $\mathbf{\theta }$ 包含了权重向量 $\mathbf{w}$ 和偏置 $b$。
  如果 $\mathbf{\varphi }(\mathbf{x})$ 本身是可学习的基函数，例如：

$${\varphi }_k(\mathbf{x})=h({\mathbf{w}}_k^T{\mathbf{\varphi }}^{\prime }(\mathbf{x})+b_k)$$其中，$h(\cdot )$ 是非线性函数，${\mathbf{\varphi }}^{\prime }(\mathbf{x})$ 是另一组基函数，${\mathbf{w}}_k$ 和 $b_k$ 是可学习的参数，那么模型 $f(\mathbf{x};\mathbf{\theta })$ 就等价于神经网络模型。

2. 学习准则

a. 损失函数

b. 风险最小化准则

【深度学习】机器学习概述（一）机器学习三要素——模型、学习准则、优化算法

3. 优化

机器学习问题转化成为一个最优化问题

  一旦确定了训练集 $\mathcal{D}$、假设空间 $\mathcal{F}$ 以及学习准则，接下来的任务就是通过优化算法找到最优的模型 $f(\mathbf{x},{\mathbf{\theta }}^{\ast })$。机器学习的训练过程本质上是最优化问题的求解过程。

a. 参数与超参数

  优化可以分为参数优化和超参数优化两个方面：

1. 参数优化： $(\mathbf{x};\mathbf{\theta })$ 中的 $\mathbf{\theta }$ 称为模型的参数，这些参数通过优化算法进行学习。这些参数可以通过梯度下降等算法迭代地更新，以使损失函数最小化。

2. 超参数优化： 除了可学习的参数 $\mathbf{\theta }$ 外，还有一类参数用于定义模型结构或优化策略，这些参数被称为超参数。例如，聚类算法中的类别个数、梯度下降法中的学习率、正则化项的系数、神经网络的层数、支持向量机中的核函数等都是超参数。与可学习的参数不同，超参数的选取通常是一个组合优化问题，很难通过优化算法自动学习。通常，超参数的设定是基于经验或者通过搜索的方法对一组超参数组合进行不断试错调整。

b. 梯度下降法

  在机器学习中，最简单而常用的优化算法之一是梯度下降法。梯度下降法用于最小化一个函数，通常是损失函数或者风险函数。这个函数关于模型参数（权重）的梯度指向了函数值增加最快的方向，梯度下降法利用这一信息来更新参数，使得函数值逐渐减小。

梯度下降法的迭代公式

$${\mathbf{\theta }}_{t+1}={\mathbf{\theta }}_t-\alpha \frac{\partial {\mathcal{R}}_{\mathcal{D}}(\mathbf{\theta })}{\partial \mathbf{\theta }}$$

其中：

• ${\mathbf{\theta }}_t$ 是第 (t) 次迭代时的参数值。
• $\alpha$ 是学习率，控制参数更新的步长。
• ${\mathcal{R}}_{\mathcal{D}}(\mathbf{\theta })$ 是风险函数，也可以是损失函数，表示在训练集 (\mathcal{D}) 上的性能。

梯度下降法的目标是通过迭代调整参数，使得风险函数最小化。

具体的参数更新公式

参数更新公式可以具体化为：

$${\mathbf{\theta }}_{t+1}={\mathbf{\theta }}_t-\alpha \frac{1}{N}\sum _{n=1}^N\frac{\partial \mathcal{L}(y^{(n)},f({\mathbf{x}}^{(n)};\mathbf{\theta }))}{\partial \mathbf{\theta }}$$

其中：

• $N$ 是训练集中样本的数量。
• $\mathcal{L}(y^{(n)},f({\mathbf{x}}^{(n)};\mathbf{\theta }))$ 是损失函数，表示模型对样本 $n$ 的预测误差。

学习率的选择

  学习率 $\alpha$ 是一个关键的超参数，影响着参数更新的步长。选择合适的学习率很重要，过小的学习率可能导致收敛速度过慢，而过大的学习率可能导致参数在优化过程中发散。

  梯度下降法的一种改进是使用自适应学习率的变体，如 Adagrad、RMSprop 和 Adam 等。这些算法能够根据参数的历史梯度自动调整学习率，从而更灵活地适应不同参数的更新需求。

c. 随机梯度下降

批量梯度下降法 (BGD)

  在批量梯度下降法中，每一次迭代都要计算整个训练集上的梯度，然后更新模型参数，这导致了在大规模数据集上的高计算成本和内存要求。其迭代更新规则如下：

$${\theta }_{t+1}={\theta }_t-\alpha \nabla {\mathcal{R}}_{\mathcal{D}}({\theta }_t)$$

其中，$\alpha$ 是学习率，$\nabla {\mathcal{R}}_{\mathcal{D}}({\theta }_t)$ 是整个训练集上损失函数关于参数 ${\theta }_t$ 的梯度。

随机梯度下降法 (SGD)

  随机梯度下降法通过在每次迭代中仅使用一个样本来估计梯度，从而减小了计算成本。其迭代更新规则如下：

$${\theta }_{t+1}={\theta }_t-\alpha \nabla \mathcal{L}({\theta }_t,{\mathbf{x}}_i,y_i)$$

其中，$\nabla \mathcal{L}({\theta }_t,{\mathbf{x}}_i,y_i)$ 是单个样本 $({\mathbf{x}}_i,y_i)$ 上的损失函数关于参数 ${\theta }_t$ 的梯度。

小批量梯度下降法 (Mini-batch Gradient Descent)

  为了权衡计算成本和梯度估计的准确性，通常使用小批量梯度下降法。该方法在每次迭代中使用一个小批量（mini-batch）样本来估计梯度，从而兼具计算效率和梯度准确性。

$${\theta }_{t+1}={\theta }_t-\alpha \nabla {\mathcal{L}}_{\text{batch}}({\theta }_t,\text{Batch})$$

其中，$\nabla {\mathcal{L}}_{\text{batch}}({\theta }_t,\text{Batch})$ 是小批量样本集 $\text{Batch}$ 上的损失函数关于参数 ${\theta }_t$ 的梯度。

SGD 的优势

1. 计算效率： 相对于批量梯度下降法，SGD的计算成本更低，尤其在大规模数据集上更为实用。

2. 在线学习： SGD具有在线学习的性质，每次迭代只需一个样本，使得模型可以逐步适应新数据。

3. 跳出局部极小值： 由于每次迭代使用的样本不同，SGD有助于跳出局部极小值，从而更有可能找到全局最优解。

SGD 的挑战

1. 不稳定性： SGD中每次迭代的更新可能受到单个样本的影响，导致更新方向波动较大。

2. 学习率调整： 选择合适的学习率对于SGD的性能至关重要。学习率过大可能导致不稳定性，而学习率过小可能使模型收敛缓慢。

3. 需调参： SGD的性能依赖于学习率、小批量大小等超参数的选择，需要进行调参。

在实践中，通常会使用学习率衰减、动量法等技术来改进SGD的性能。