前言

当我们自动化用例写完后，接下来就是如何运行用例，生成报告以及反馈通知了。
如果你们公司已经有jenkins了，那么直接集成到jenkins上构建你的自动化任务是非常方便的。

用例上传git仓库

第一步，将写好的自动化用例，上传到本公司的git仓库。

jenkins 自动拉取仓库代码

在jenkins上创建一个自由风格的项目

源码管理，添加git自动化项目地址

构建步骤执行pytest命令，生成allure报告

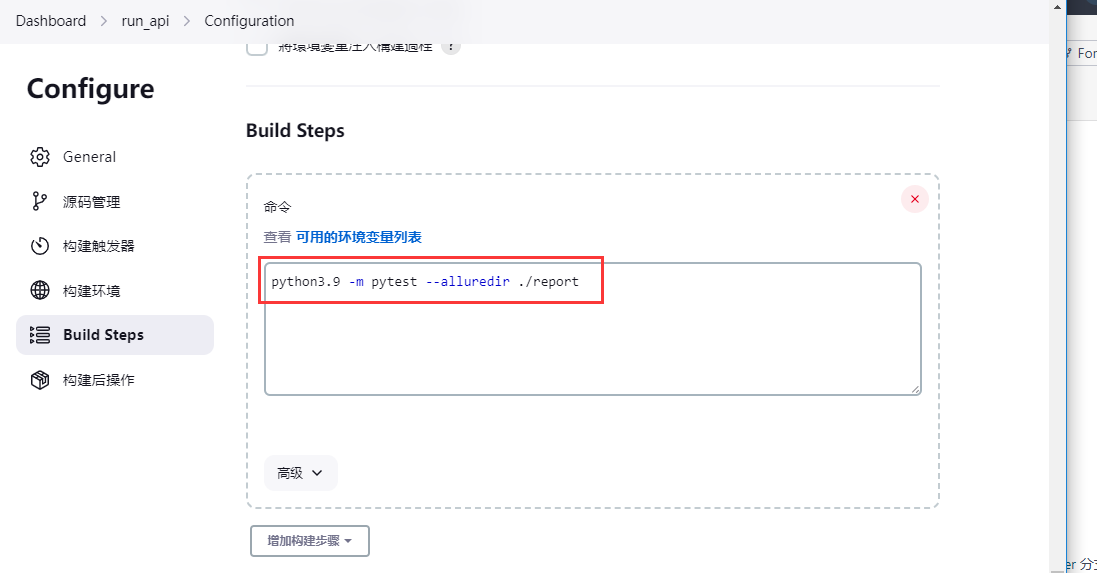
生成allure报告

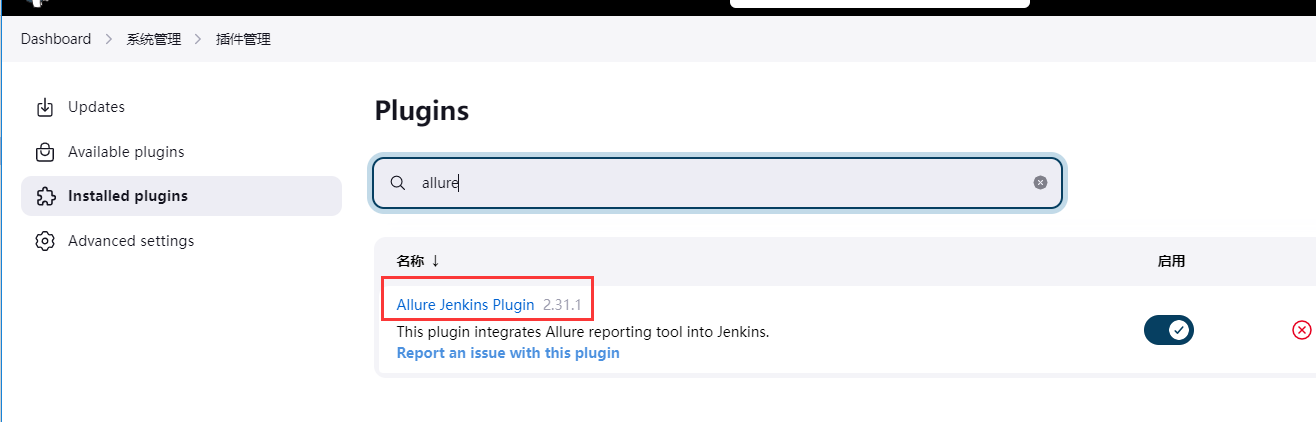
插件管理搜索：allure， 安装 allure 插件

系统管理-全局工具管理，安装allure命令行工具

构建后操作，添加allure报告，报告地址跟前面一步--alluredir 设置的地址保存一致即可.

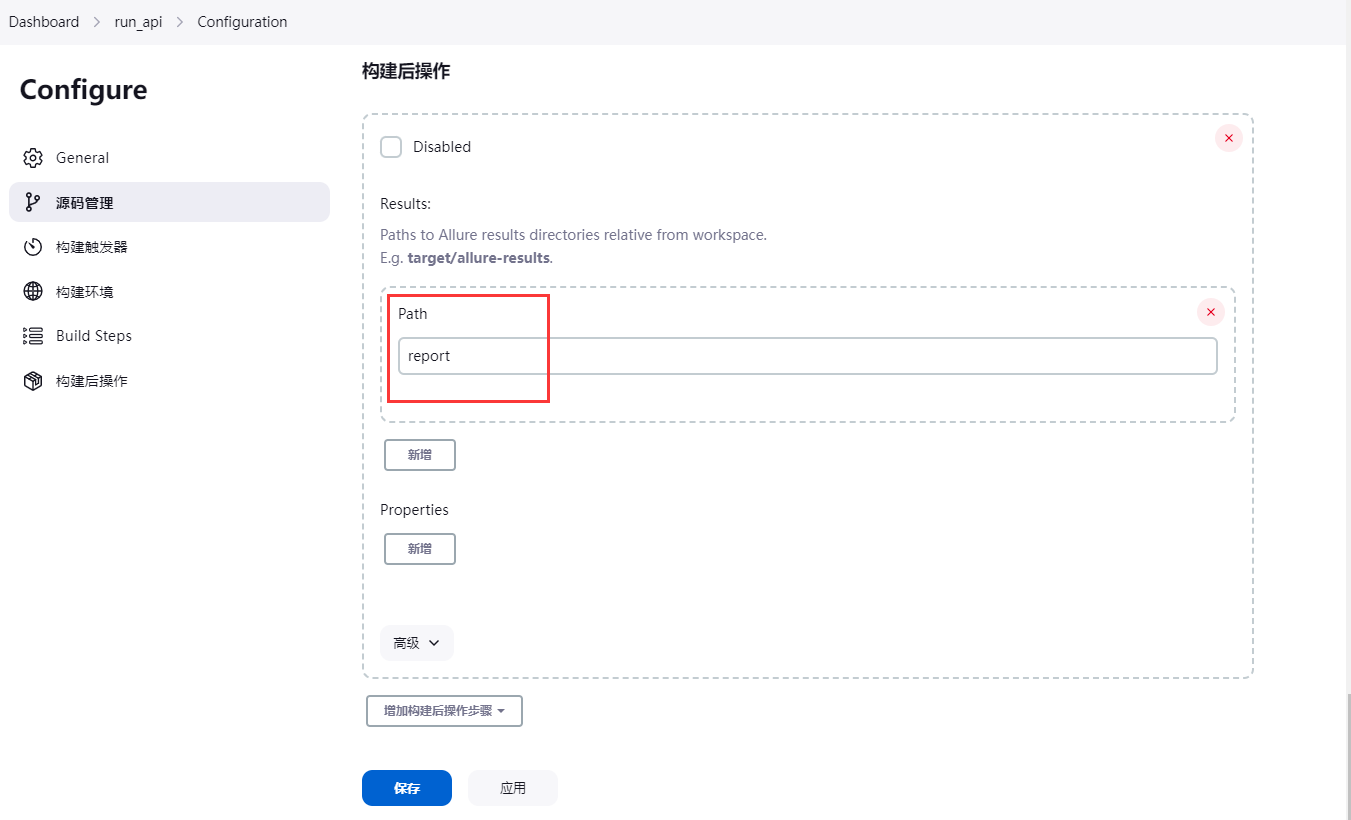
构建后即可查看 allure 报告

钉钉通知

系统管理-插件管理，搜索钉钉插件:DingTalk

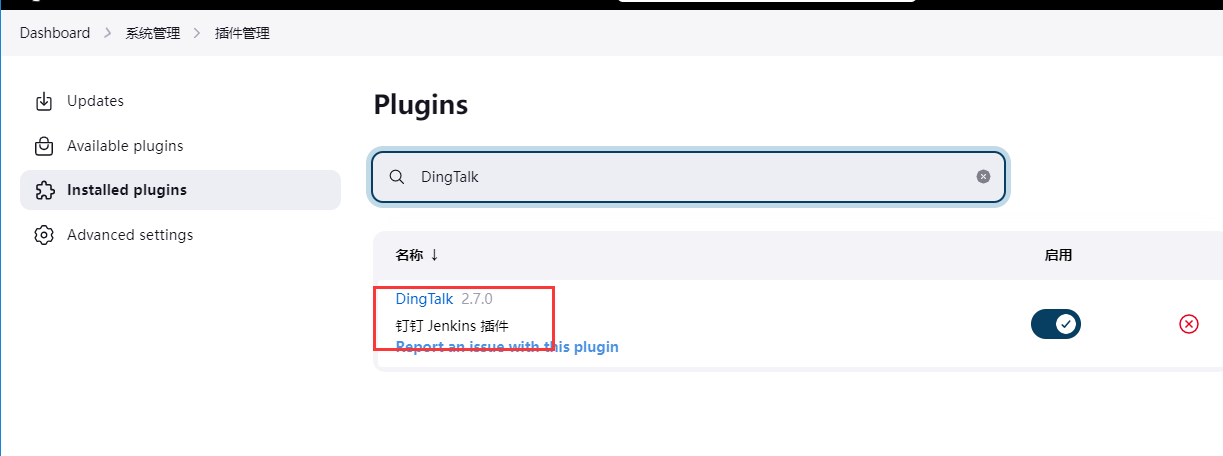
系统管理，拖到最底部，找到钉钉配置

配置以下3个地方：

1.名称自定义:yoyo
2.webhook地址，在钉钉群里添加机器人后找到：

3.关键字:也是钉钉群机器人设置的关键字保存一致

添加完成后点测试按钮，可以看到钉钉群消息发送成功

接下来配置项目job执行完成后钉钉消息反馈
添加钉钉机器人

点开高级，可以配置发送的消息内容，以及接收人

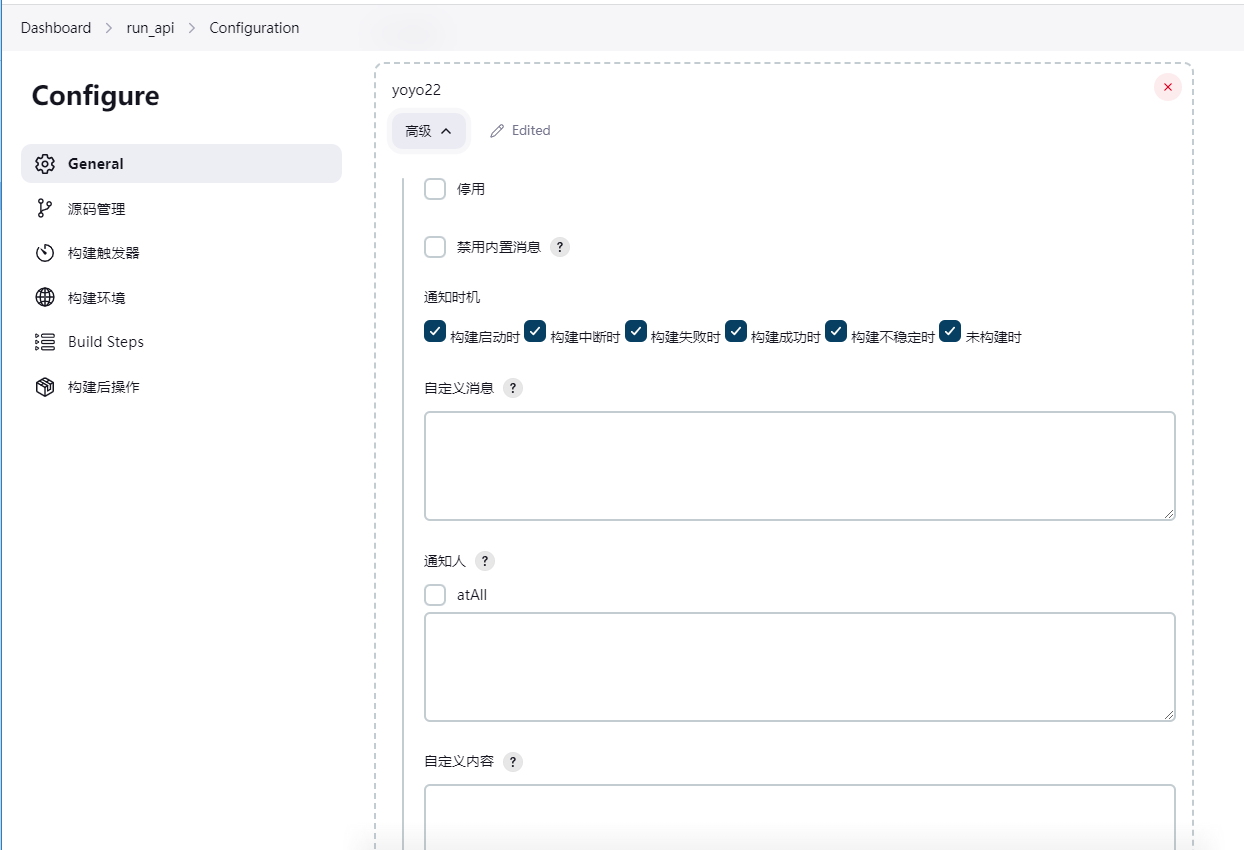
其中自定义内容（消息通知内容）支持 Markdown 语法，内容如下

- 测试报告：${BUILD_URL}allure
- 构建日志地址：${BUILD_URL}console

构建时机，选择构建之后触发

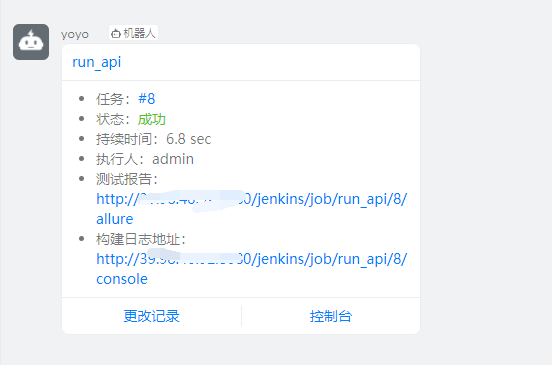
构建完成后可以看到以下通知，点报告地址查看详情

网易云完整视频课程https://study.163.com/course/courseMain.htm?courseId=1213419817&share=2&shareId=480000002230338
报名咨询wx:283340479 (已报名的同学学习过程中有问题，都可以协助解决)