clickhouse一次排错

clickhouse启动报错

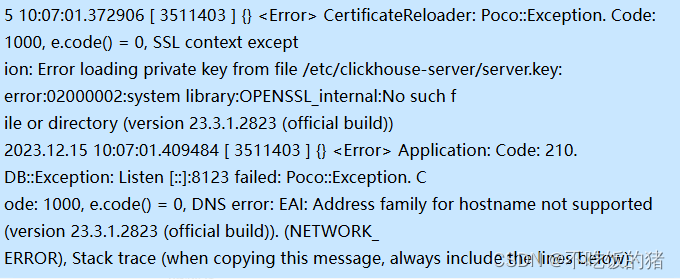
1. 报错：

Application: Code: 210. DB::Exception: Listen [::]:8123 failed: Poco::Exception. Code: 1000, e.code() = 0, DNS error: EAI: Address family for hostname not supported (version 23.3.1.2823 (official build)). (NETWORK_ERROR), Stack trace (when copying this message, always include the lines below):
【说明本机没有开放ipv6，只能对ipv4生效。需要改coinfig的配置】
2，排查config文件
/etc/clickhouse-server/config.xml

需要修改listen_host

3.启动成功