文章目录
- 图的基本操作
- 总览
- 找边
- 列出与某顶点相连的边
- 插入顶点
- 删除顶点
- 增加边
- 顶点的第一个邻接点
- 顶点的下一个邻接点
- 设置或者获取某条边的权值
- 总览
- 图的广度优先遍历
- 总览
- 树的广度优先遍历
- 图的广度优先遍历
- 树vs图
- 图广度优先遍历的代码实现
- 广度优先遍历序列
- 遍历序列的可变性
- 算法存在问题
- 改进后的 复杂度分析
- 广度优先生成树
- 广度优先生成森林
- 练习:有向图的BFS
- 小结
- 图的深度优先遍历
- 总览
- 树的深度优先遍历
- 图的深度优先遍历
- 算法存在的问题
- 复杂度分析
- 深度优先遍历序列
- 深度优先生成树
- 深度优先生成森林
- 图的遍历与图的连通性
- 小结
图的基本操作
总览

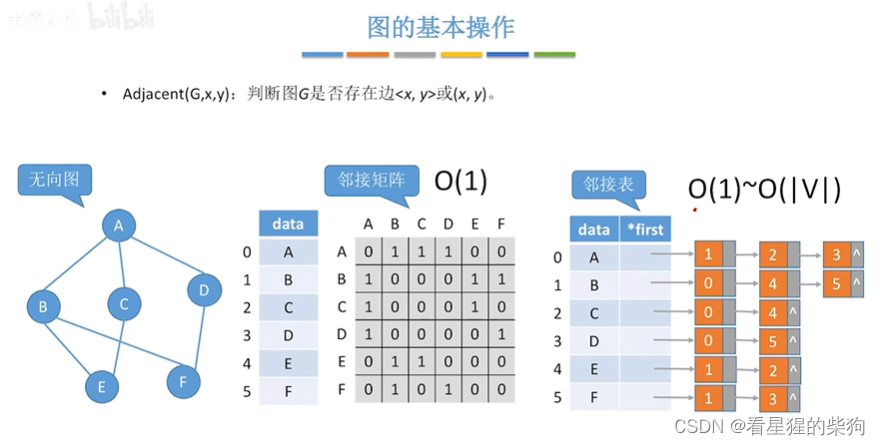
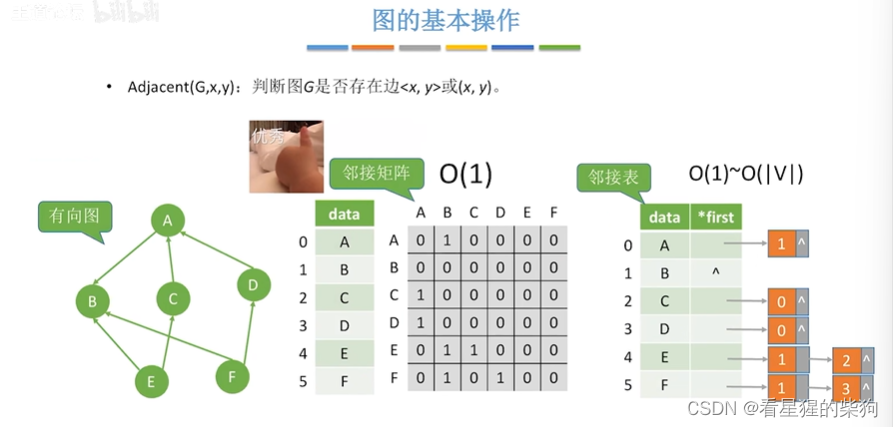
找边
邻接矩阵直接找图中的某个元素是否为1即可
邻接表要遍历顶点的边链表
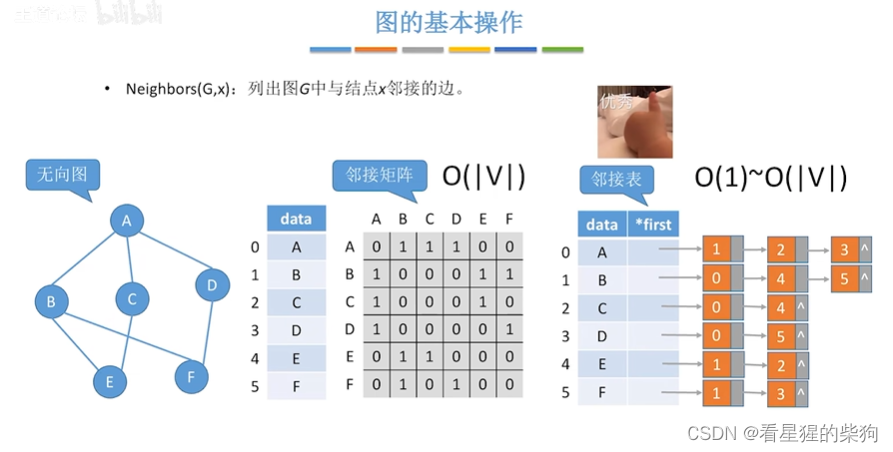
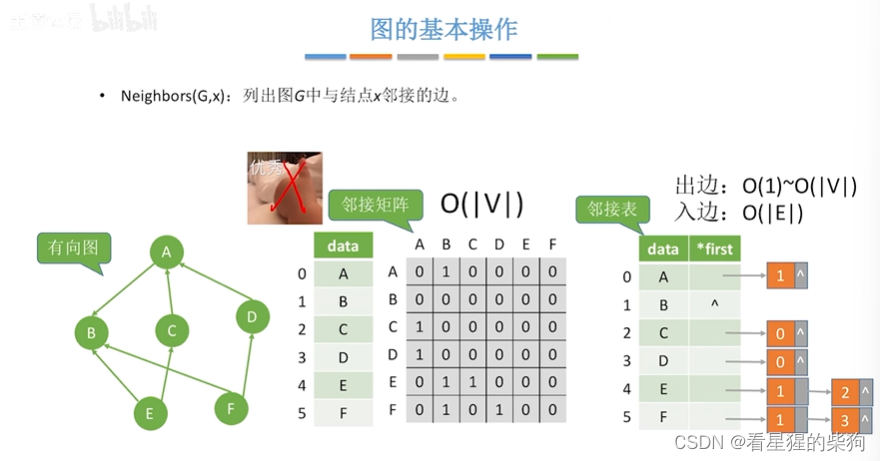
列出与某顶点相连的边
邻接矩阵找行或列
邻接表找顶点对应的边链表
对于有向图的邻接表的入边时候需要将其他顶点的边链表都遍历
插入顶点
此时插入的是与其他顶点都没有连接的顶点
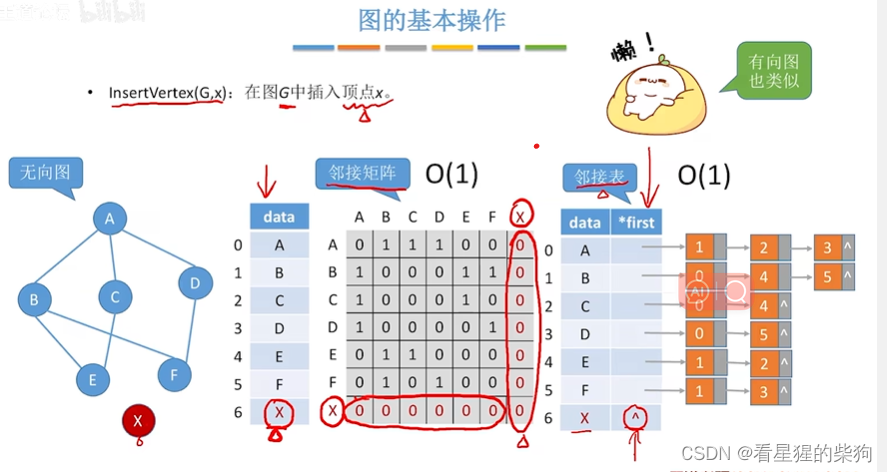
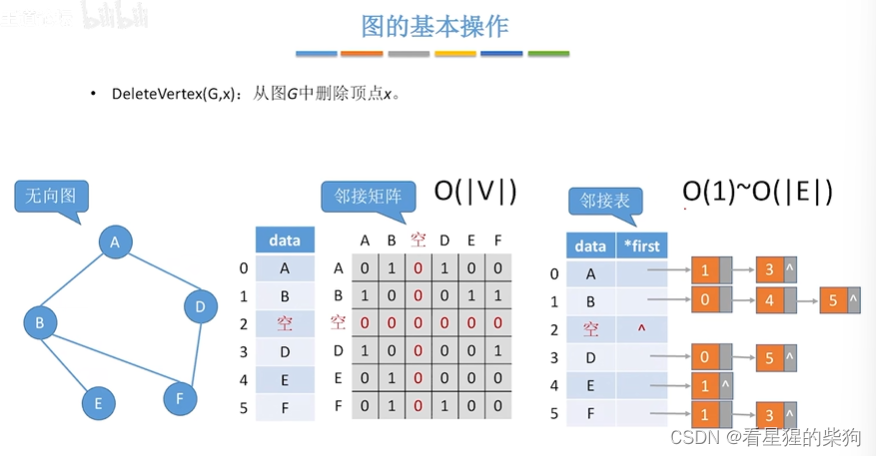
删除顶点
邻接矩阵设置 顶点中的一个变量为布尔型变量用来标记该顶点是否有效,当删除该节点时,只需将该节点所在行和列设置为0即可
邻接表即遍历所有边链表,将有顶点的边都删除,并修改对于的边链表
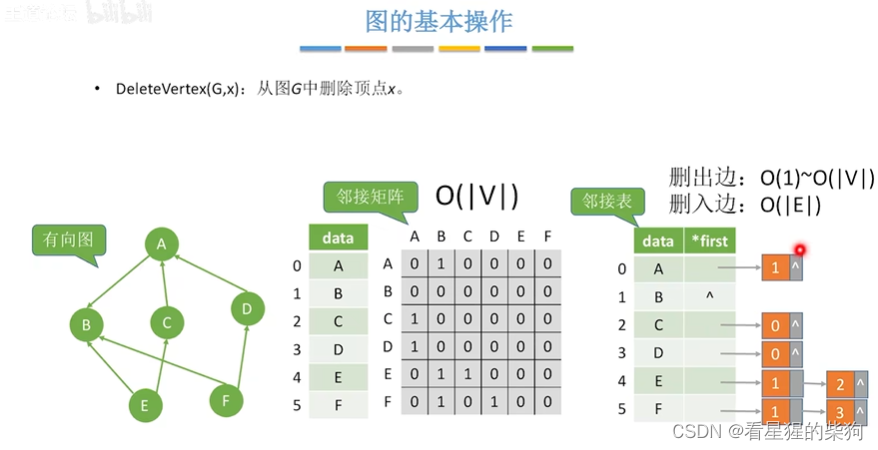
增加边
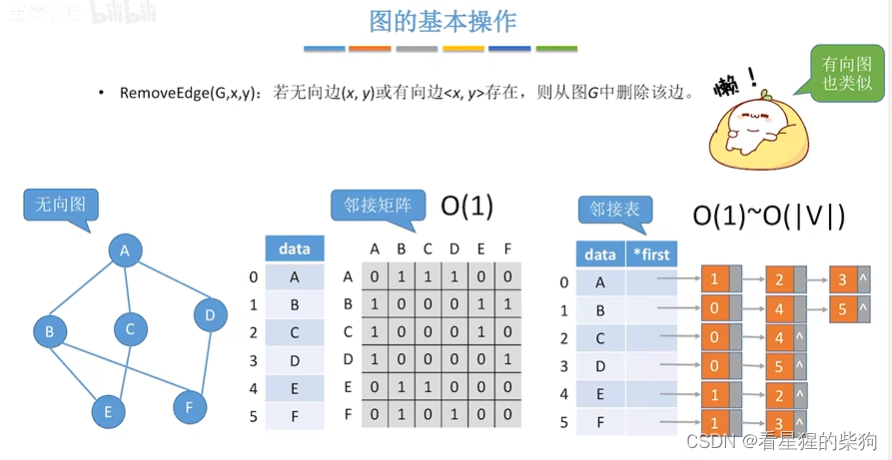
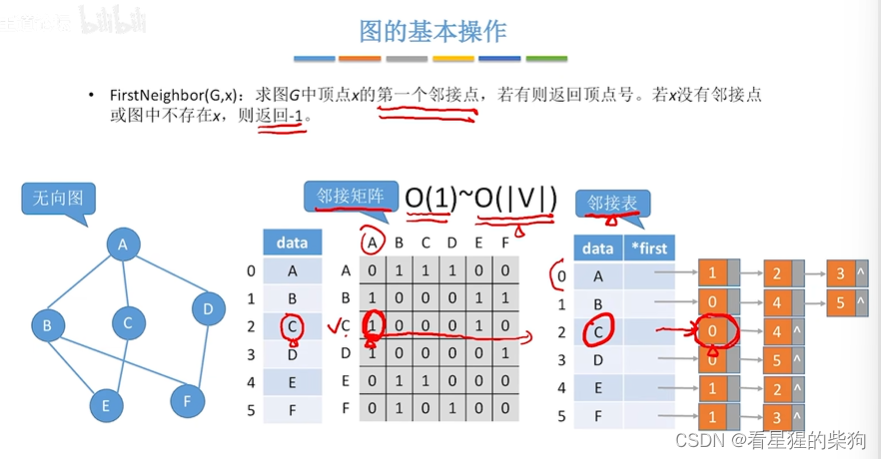
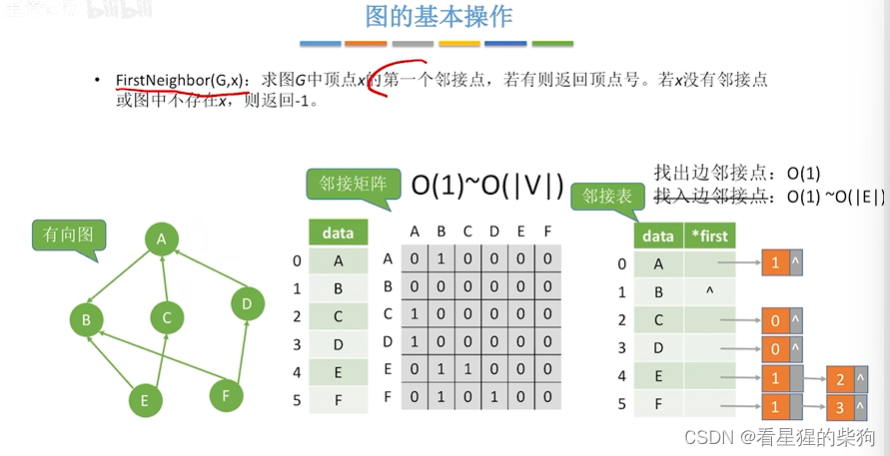
顶点的第一个邻接点
就是遍历到的第一个
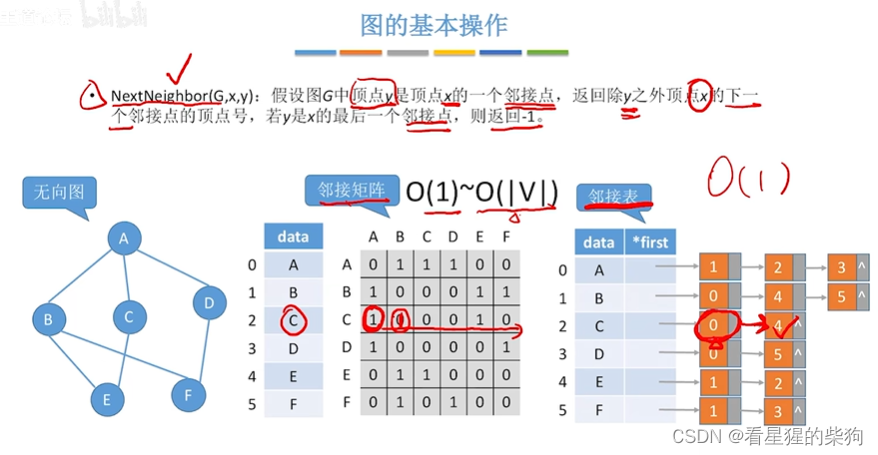
顶点的下一个邻接点
就是遍历到的第二个
设置或者获取某条边的权值

总览

图的广度优先遍历
总览

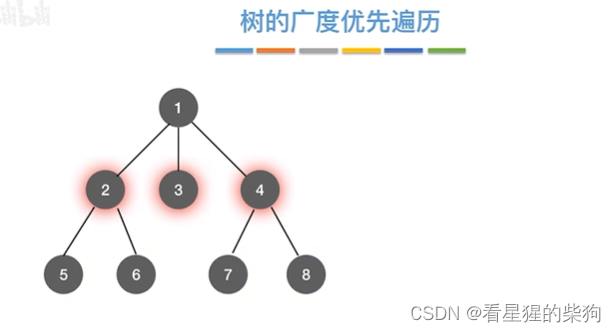
树的广度优先遍历
即找根节点的孩子节点先
图的广度优先遍历
即先访问节点的相邻节点
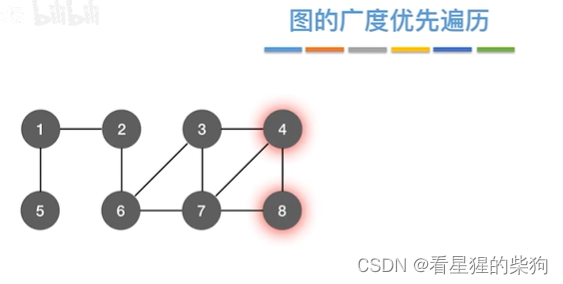
树vs图
图遍历可能访问到原先的节点,但树不会,因为它是一直访问孩子节点的

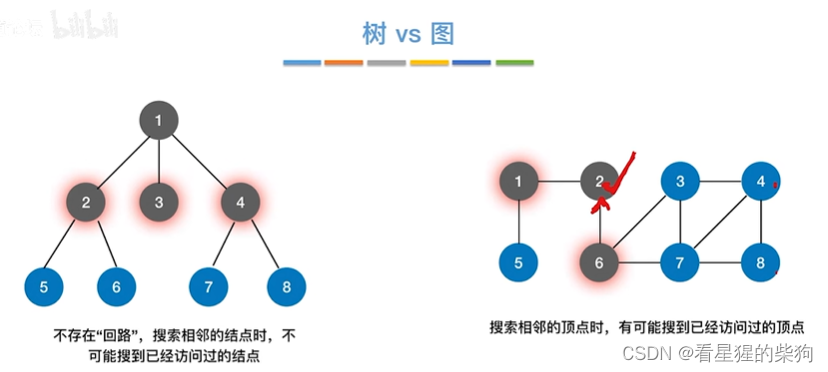
图广度优先遍历的代码实现
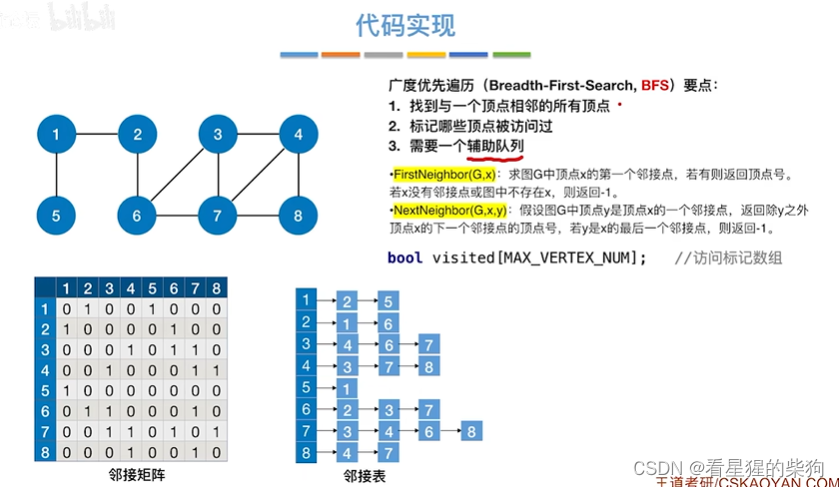
访问后入队,然后出队后再将其相邻且没有访问的节点访问,然后再入队,然后再出队再将其相邻且没有访问的节点访问,如此反复
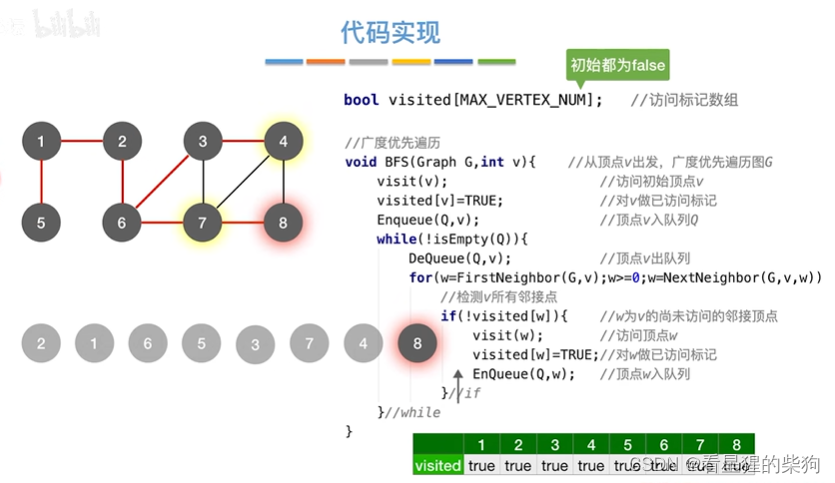
广度优先遍历序列
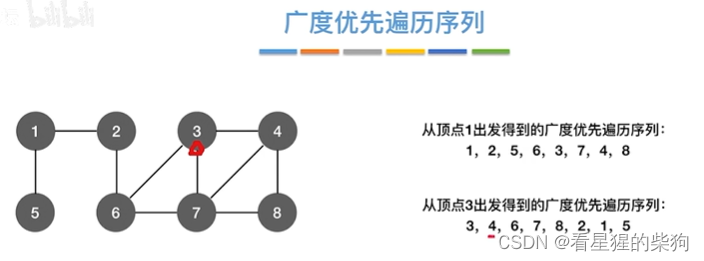
遍历序列的可变性
不同邻接表对应的遍历序列可能不一样
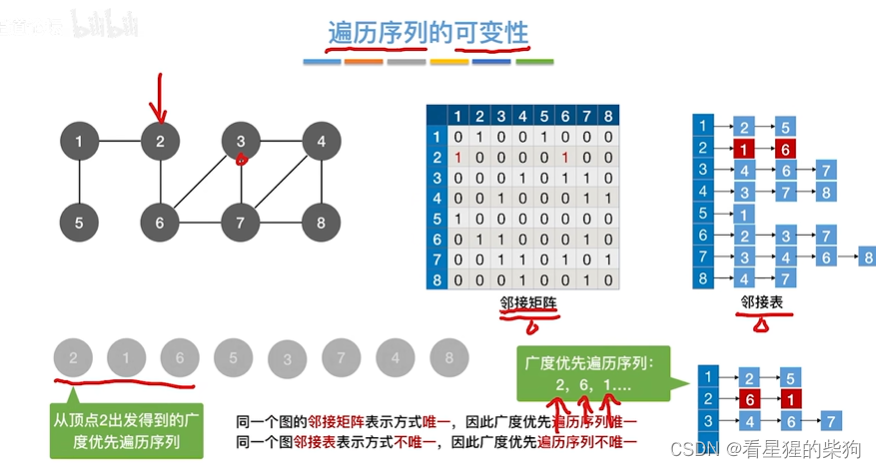
算法存在问题
非连通图无法遍历完所有节点
解决方法就是每个节点都广度优先遍历
下面是改进
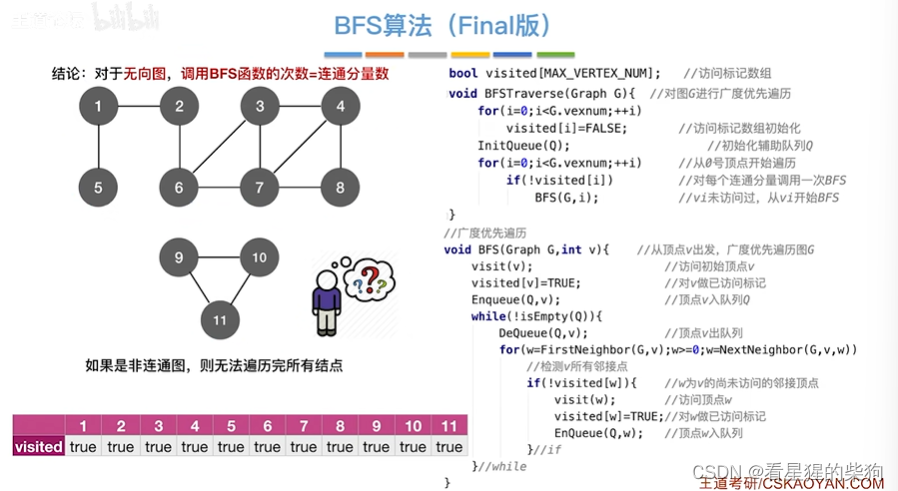
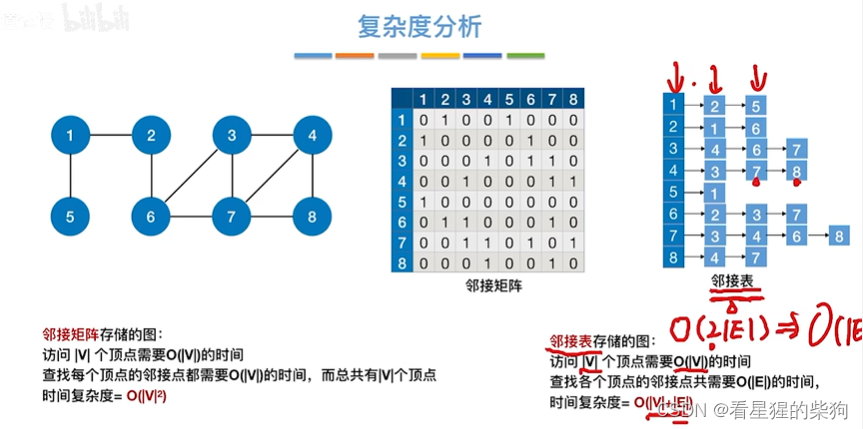
改进后的 复杂度分析
从结点树和边数考虑(从访问顶点和找各条边考虑)
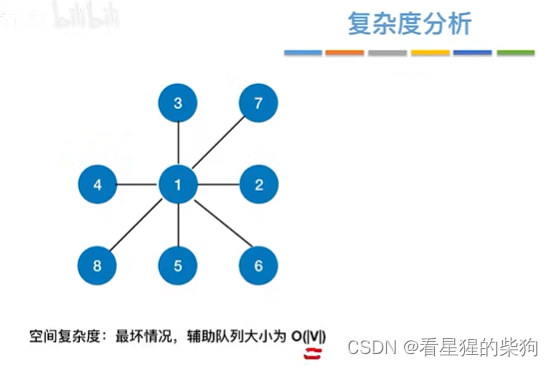
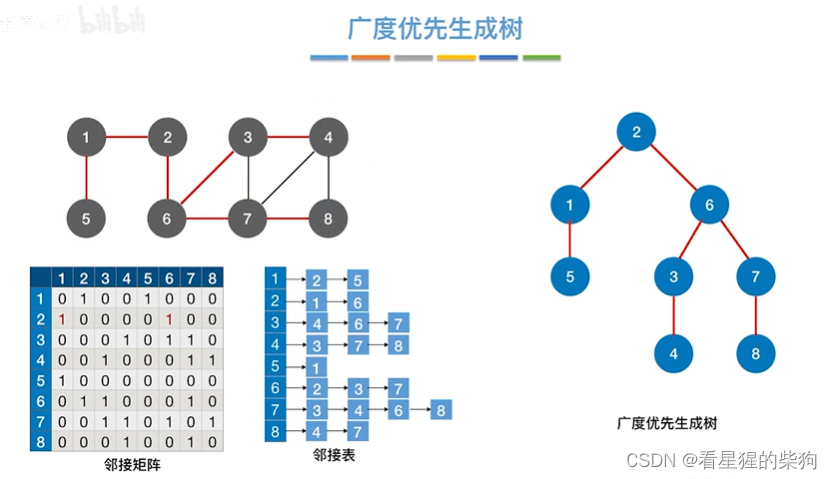
广度优先生成树
广度优先遍历过程生成的
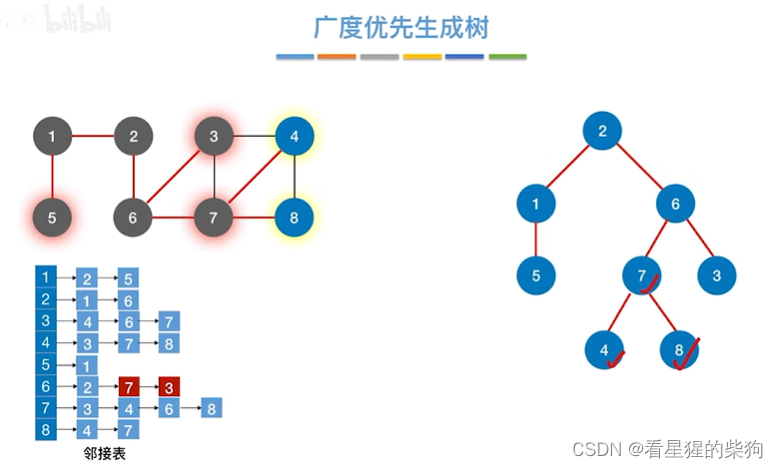
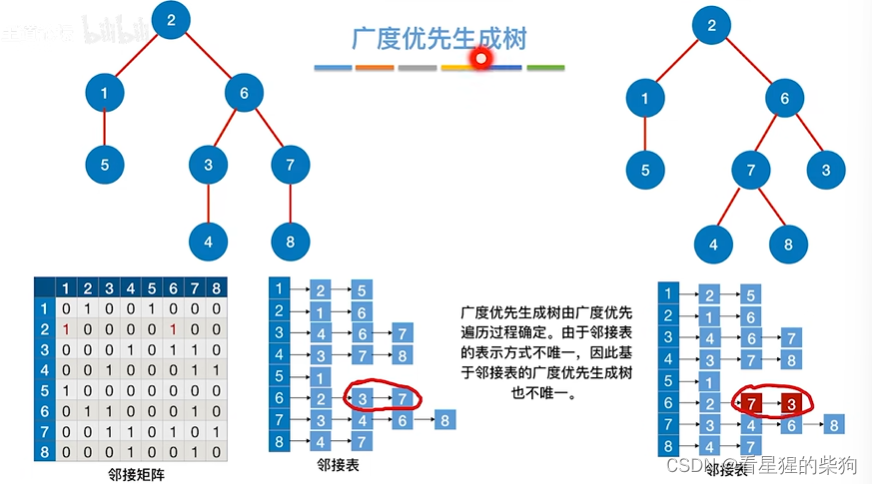
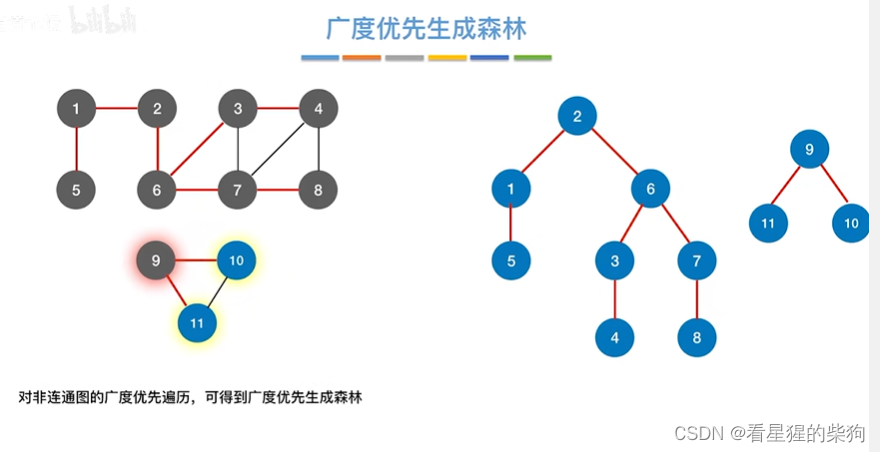
广度优先生成森林
即对各个连通分量广度优先遍历即可
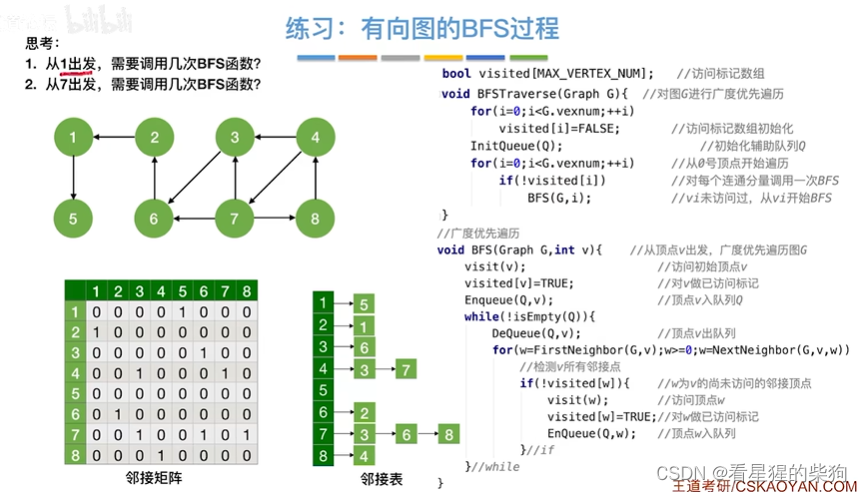
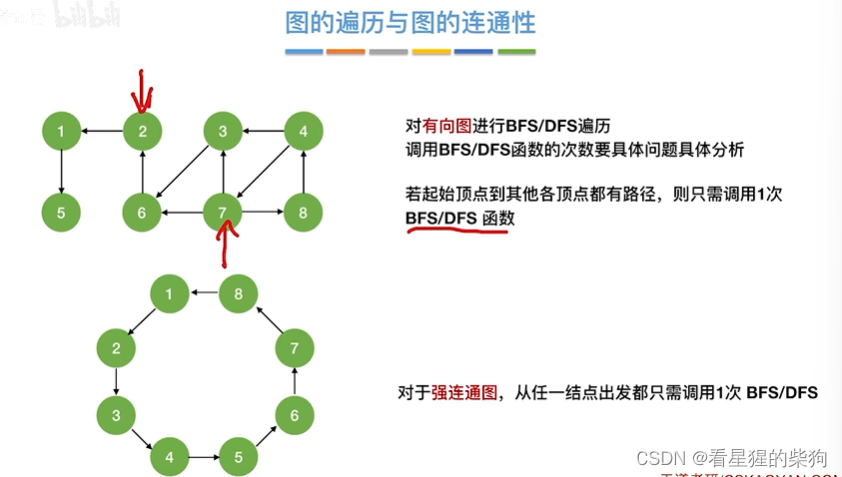
练习:有向图的BFS
有些点BFS不能遍历完所有的结点
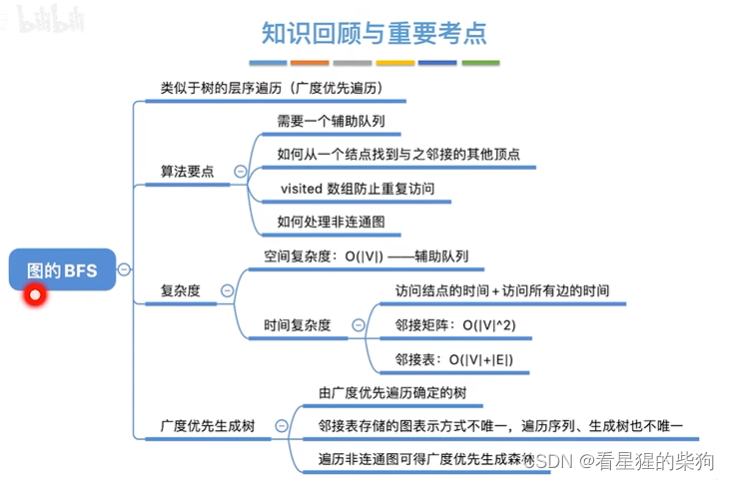
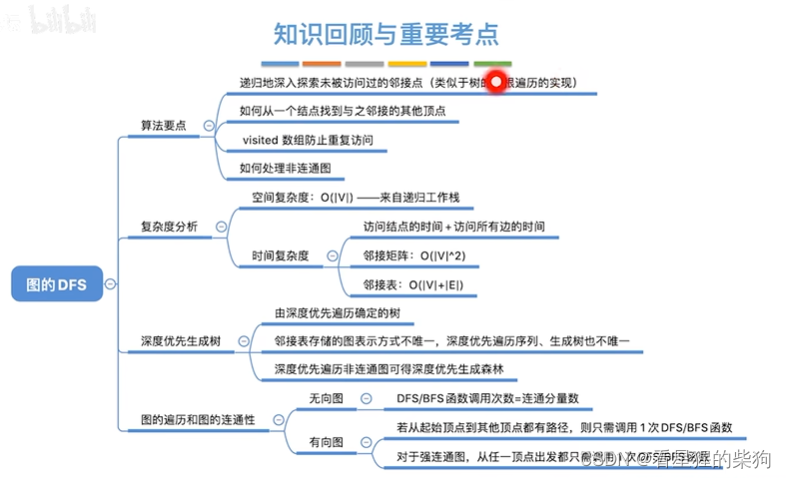
小结
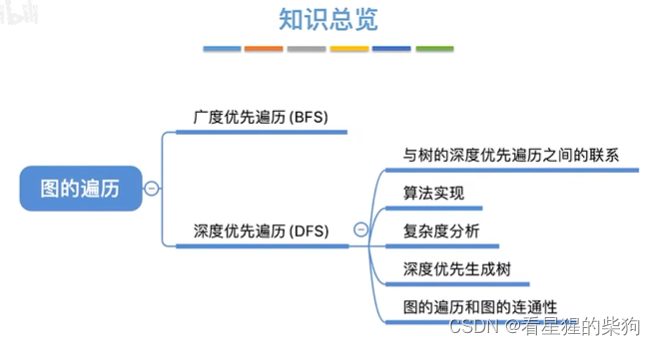
图的深度优先遍历
总览
树的深度优先遍历
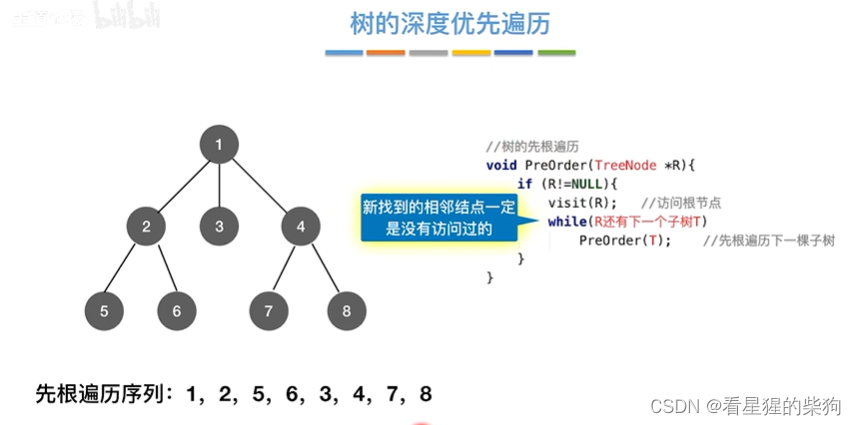
图的深度优先遍历
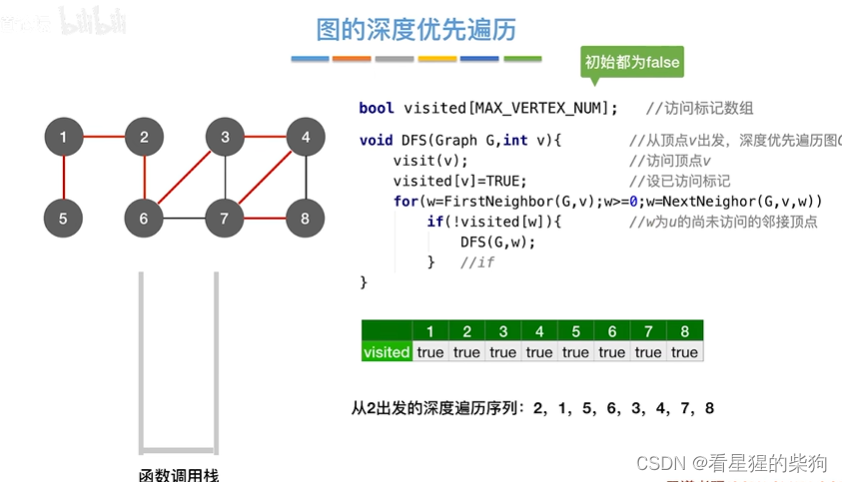
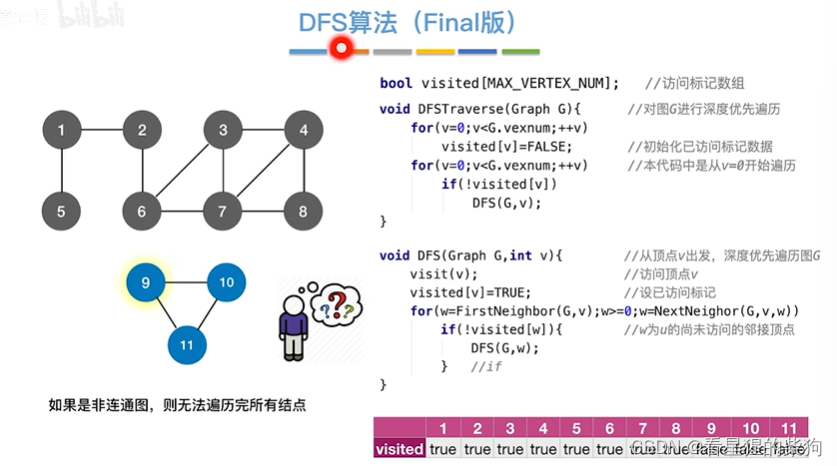
算法存在的问题
依然是所有顶点都深度优先遍历一次
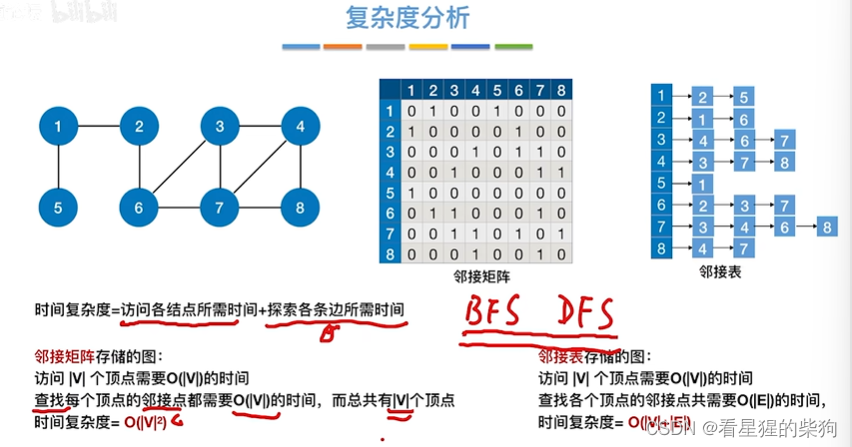
复杂度分析
即可能同时调用V次代码(或者说来自递归工作栈)
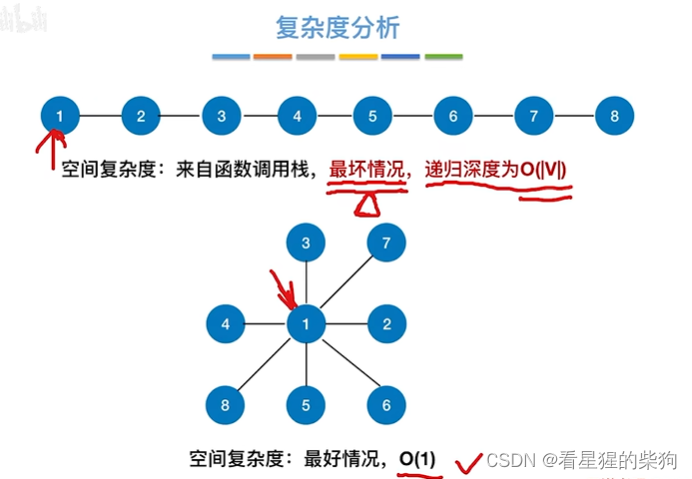
即每个结点最终都会进入一次深度优先遍历函数,这样才可能最终深度优先遍历所有节点
只不过邻接矩阵中对应节点进入函数后时间复杂度为V
而邻接表为E
深度优先遍历序列
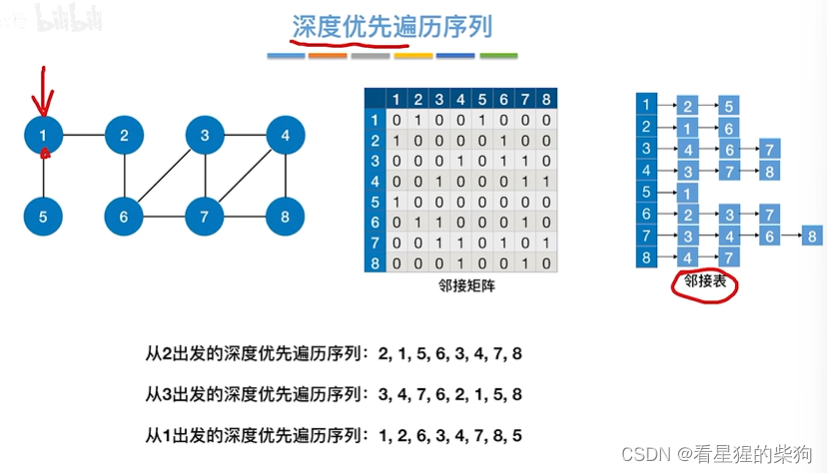
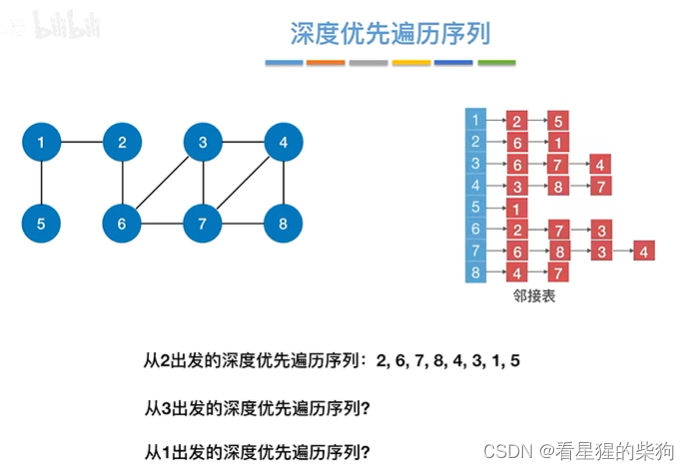
邻接表不一样,深度优先遍历序列可能不一样
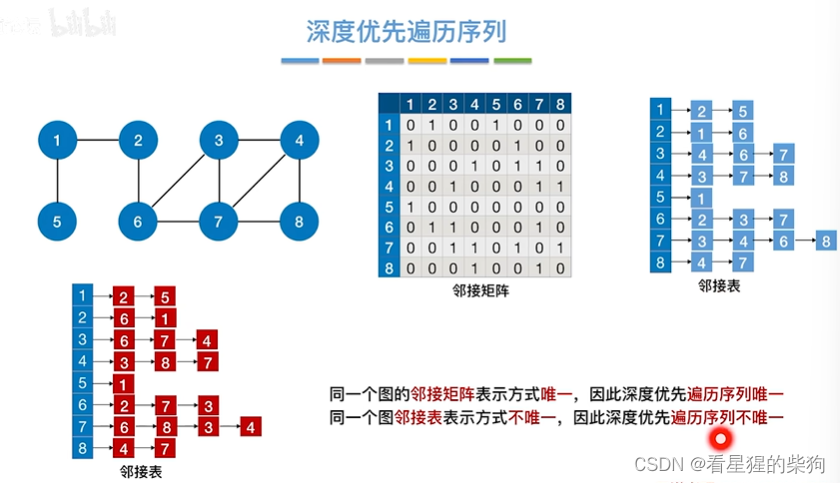
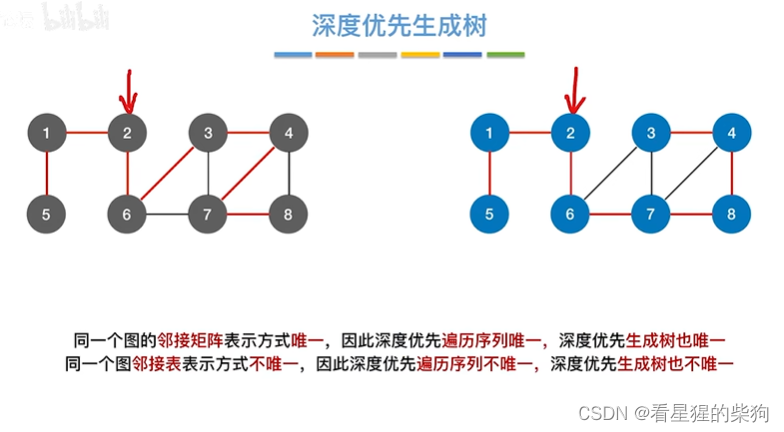
深度优先生成树
同样,即将遍历序列的其他边去了即可
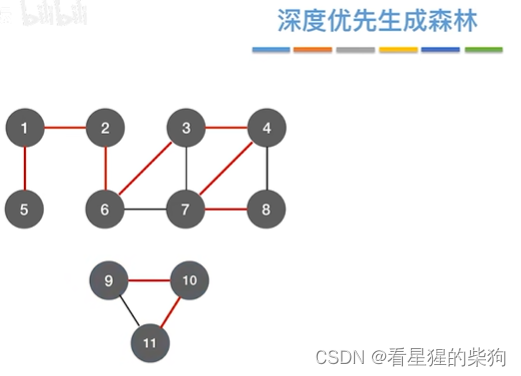
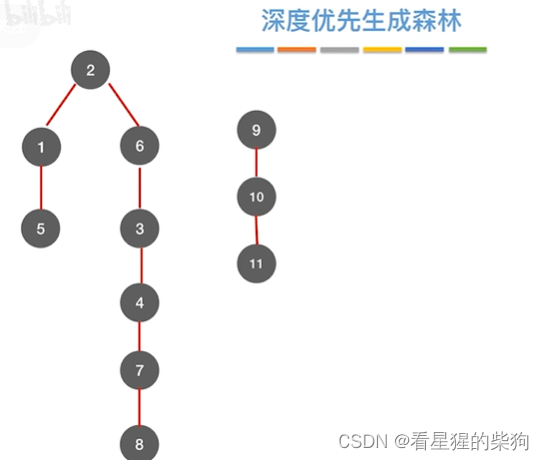
深度优先生成森林
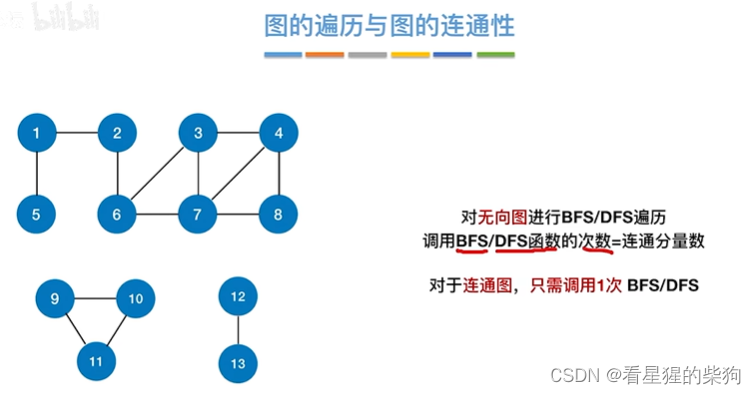
图的遍历与图的连通性
小结










:面向对象)

)






