文章信息

论文题目为《城轨线路列车时刻表与车站客流控制协同优化方法》，该文于2021年发表于《交通运输系统工程与信息》上。文章考虑换入客流影响下列车时刻表与客流控制的协同优化问题，以最小化乘车延误人数为目标，以列车时刻表、客流控制和动态载客为约束条件，建立非线性规划模型，引入0-1决策变量将其转化为整数线性规划模型并求解。

摘要

在轨道交通网络化运营条件下，针对高峰期车站拥挤问题，综合考虑站外到达乘客的持续 性到达特征和换入客流的脉冲性到达特征，研究换入客流影响下的列车时刻表与客流控制问题。具体的，以最小化乘车延误人数为目标，考虑乘客换乘约束、列车容量约束等，构建城轨列车时刻表与客流控制协同优化非线性规划模型，并引入0-1决策变量将其转化为整数线性规划模型。为 验证模型有效性，以某轨道交通线路实际运营数据为背景，借助优化求解器CPLEX对模型进行求 解。结果表明，本文所提方法具有良好的优化效果和计算效率，与优化前相比，乘车延误人数可显 著降低；与仅优化列车时刻表方案相比，协同优化方法可使乘车延误人数减少17.69%，可有效提升 轨道交通的服务水平，为城市轨道交通系统高质量运营提供一定的理论支撑。

01问题定义

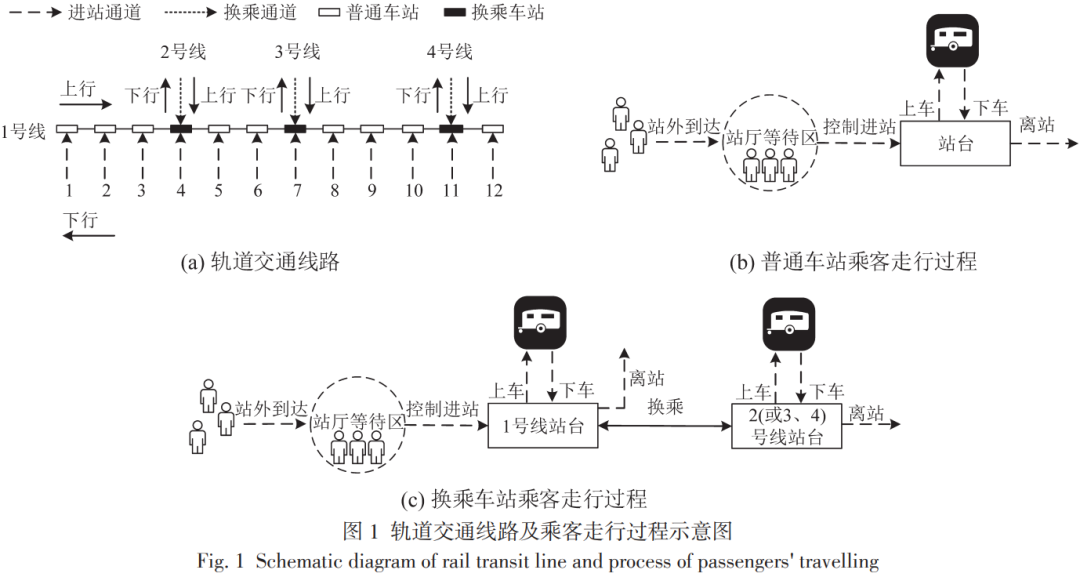
针对高峰期轨道交通车站过度拥挤问题，考虑邻接线路换入客流的影响，通过协同优化轨道交通线路列车时刻表与客流控制策略，尽可能地减少乘车延误人数。如图1所示，研究对象为主线路1号线，即图 1(a)，该线路具有图 1(b)普通车站和图 1(c)换乘车站两种类型，其中，普通车站仅有站外到达客流，换乘车站的客流则由站外到达和换入客流两部分组成。站外到达乘客需在站厅排队，等待进站指令；换入乘客可直接走行至线路 1 的站台等待上车，即换入客流优先乘车。考虑线路2、3、4换乘至主线路1乘客的影响，调整线路1的列车时刻表，使得线路1列车的到站时间与邻线列车的到站时间差接近换乘走行时间，则可使换入乘客尽量直接上车，减少站台聚集人数以降低风险。

02模型 

模型假设：

假设1：已经到达车站的乘客不会选择换乘其他交通工具。

假设2：客流需求及 OD 结构已知。在高峰时段出行的乘客大都以通勤为目的，乘客的家庭地址和工作地点相对固定，因此，通过统计分析AFC历史数据，即可获得各车站的客流需求和OD比例。

假设3：除主线路外，其他换乘线路列车时刻表不会发生改变，换入客流到站时刻及 OD 结构已知。此外，在实际运营中，高峰期允许短时过载，所以假设列车总能力大于换入客流要求。

参数及变量：

约束条件：

（1）列车时刻表约束：

列车的到发时刻需满足列车运行过程的基本约束，如下公式。

公式(1)为列车到站时刻，k=1时，为列车到达首发站的时刻；k为其他站点时，列车i到达k站点的时刻为列车离开前一个站点k-1的时刻加上列车在[k-1,k]区间上的运行时间。

公式(2)为列车的离站时刻，表示列车到达站点k的时刻加上在站点k的停站时间。

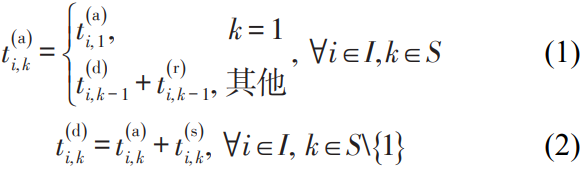
由于运行时间和停站时间是固定的，前车i 与后车i + 1在 k 车站的发车间隔由列车的离站时刻唯一确定，发车间隔只需在始发站满足上、下限约束，即

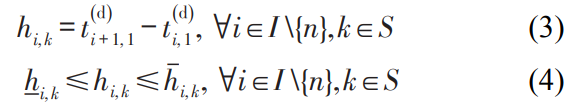
公式(3)为前车i 与后车i + 1在 k 车站的发车间隔，由后车i+1在始发站的离站时刻减去前车i在始发站的离站时刻。

公式(4)为发车间隔需要在最大和最小发车间隔之间。

（2）客流控制约束：

通过假设1当车站进行客流控制时，已到达车站站厅的乘客均不会换乘其他交通工具，所有到站乘客均被服务，即

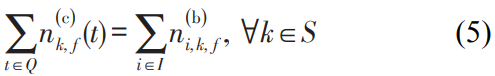
公式(5)表示所有控制时段内，在k车站的站外到达乘客均能进站乘坐列车。

假定乘客到达车站后，先在站厅排队等待，那么在k 车站的等待列车i的人数如下。

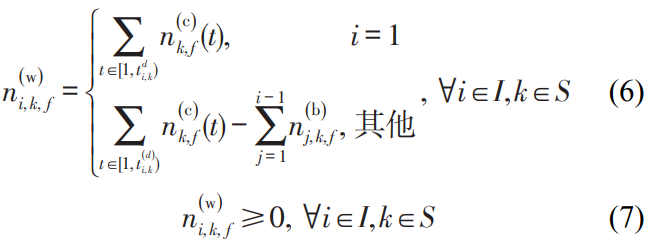
公式(6) 当第1辆列车(i=1)到达车站k时，在站厅等待的乘客数量为从1时刻到列车1从k车站离站时刻，该时间段的累积的到达客流量；当后续列车到达时，为累积的到达客流量与累积的已放入客流量之间的差值。

公式(7) 表示站厅等待的乘客数量需满足非负约束。

在客流控制策略下，当列车i到达k车站时，允许进站乘客的乘客数量一定小于等于等待的客流量，即

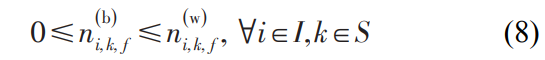
（3）动态载客约束：

动态载客过程包含乘客上、下车过程。该文假定任意车站的乘客目的地比例是既定的。

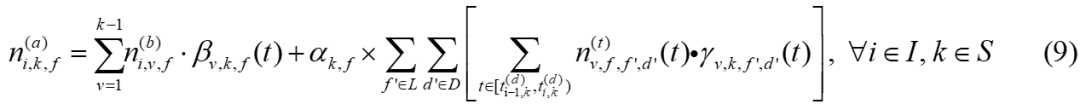
公式(9)当列车i到达k车站时，下车客流量为以该站为目的地的上游车站的上车乘客总量。具体而言，该公式由两部分组成，第一部分为k车站之前的既往车站列车i所载乘客以k车站为目的地的乘客数量。第二部分为若为换乘车站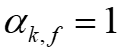，否则为0。若为换乘车站，则包含所有支线其上行下行方向，在一个发车时间间隔内，换入主线路v车站的客流(v车站为k车站前面的换乘站)乘以以k为目的地的换入客流比例。

采用客流控制措施的主要目的之一是避免站台客流积累过高，以保证乘客安全。因此，要求控制进站乘客和在站台等待的换入乘客都能够搭乘下一班列车离站。则列车i离开k车站时，车载人数为

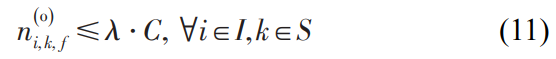
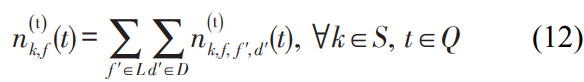
公式(10)中，k=m表示列车离开终点站时，载客量为0；k=1时表示列车i离开首发站时，车载人数包含两部分，第一是在首发站允许进入乘坐列车i的人数，第二部分是若首发站为换乘车站，则在一个发车间隔时间内其他支线上下行方向换入主线路k的客流；k为其他站点时，为列车i离开k-1车站的载客量，减去在k站下车的人数，加上在k站允许进入乘坐的人数，若为换乘站再加上一个发车间隔内从其他线的换入客流。

公式(11)表示，离开k站时的载客量需要小于等于满载系数乘以额定载客量。

公式(12)表示，k为换乘站时，从其他所有支线的上下行方向换入主线路k站的换入客流总量。

目标函数：

优化目标为沿线所有车站的乘车延误人数加和最少。乘车延误人数是指受到客流控制措 施及列车容量的限制，未能乘坐其到站后到达的首班列车离站，而需在站厅内进行二次等待的乘客人数，即为各列车驶离车站时，所有等待乘客与被服务乘客之间的差值，即

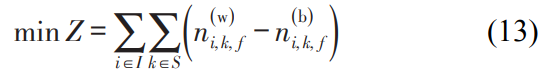
模型线性化及求解：

对于 ∀i ∈ I, ∀k ∈ S ，列车i在车站k的发车时刻 为决策变量，因此式(6)、式(9)和式(10)均为非线性约束。作者引入一组0-1变量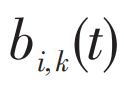进行处理，如下图所示。

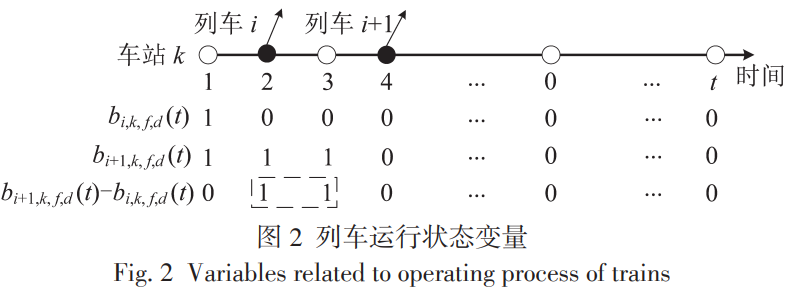
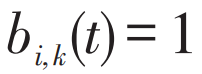表示 t 时刻列车 i 未到达且未经过 k 车站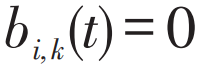，表示 t 时刻列车 i 已到达或已经过 k 车站，因此，该决策变量矩阵为非增矩阵，满足

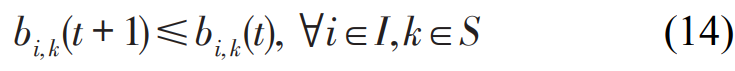
任意两相邻列车的发车间隔为其离开同一车站的时间差，如图2所示，因此，发车间隔需满足

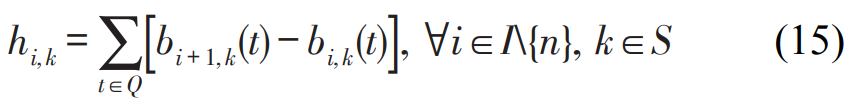
故而式(6)可转化为线性约束，即

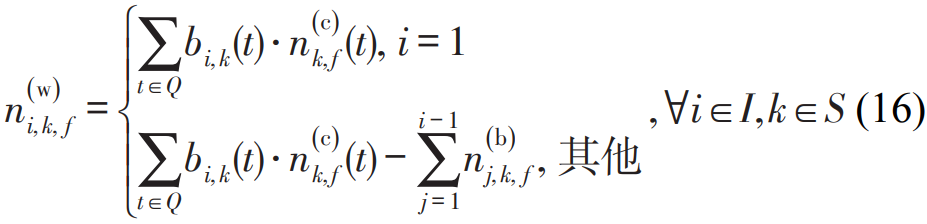
公式(16)中，i = 1 时，在时段 t 内，若列车 1 未到达或经过 k 车站，则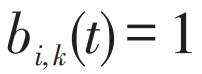，与到达乘客数量相乘即为等待客流量，反之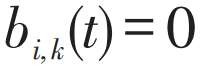，，对于列车1来说已经到达或经过k车站，就不存在等待列车1的客流。

同理，式(9)转为线性约束如下

式(10)转为线性约束如下

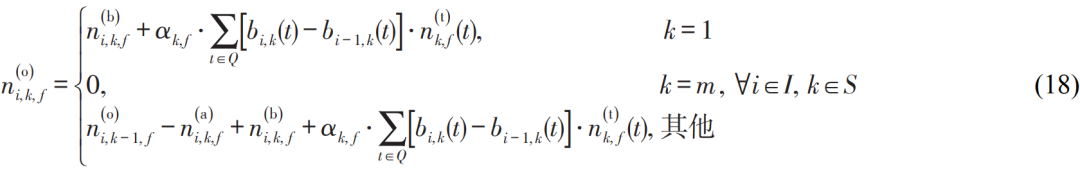
综上，作者所构建的协同优化非线性规划模型转化为标准的整数线性规划模型，利用优化求解器CPLEX，调用分支定界法对其进行快速求解。

03实验

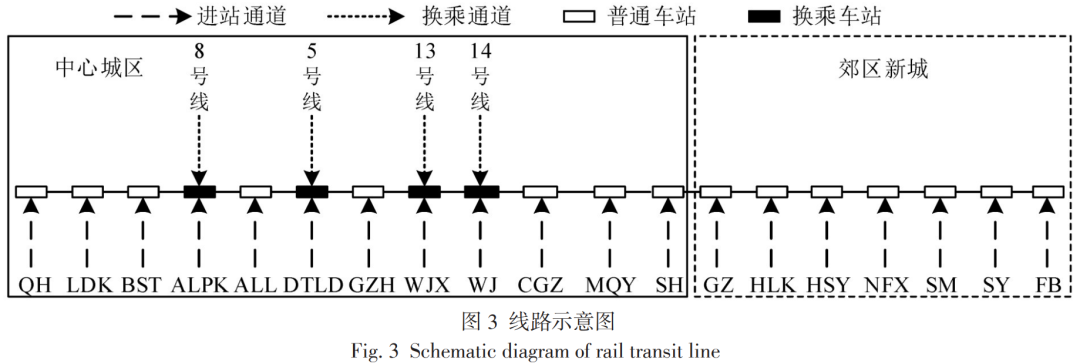
作者使用某个城市轨道交通线路的AFC刷卡数据进行实证分析。如图3所示，作者选取7:00-10:00进行研究，首先将其离散为时间粒度为 1 min 的时间区段7:00-10:00共180 个时间区段。此外，线路采用单一交路的列车运行模式和“站站停”的停站方案，停站时间作为已知参数给定。模型相关参数如表所示。

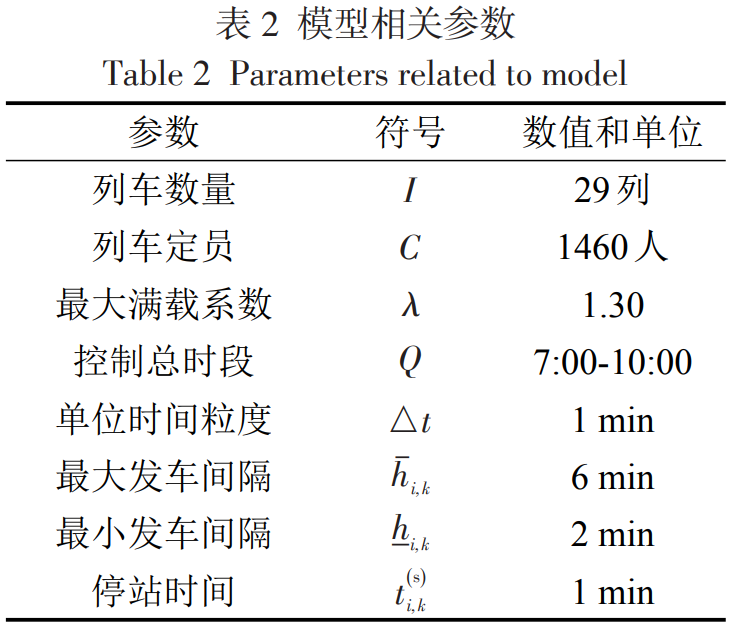
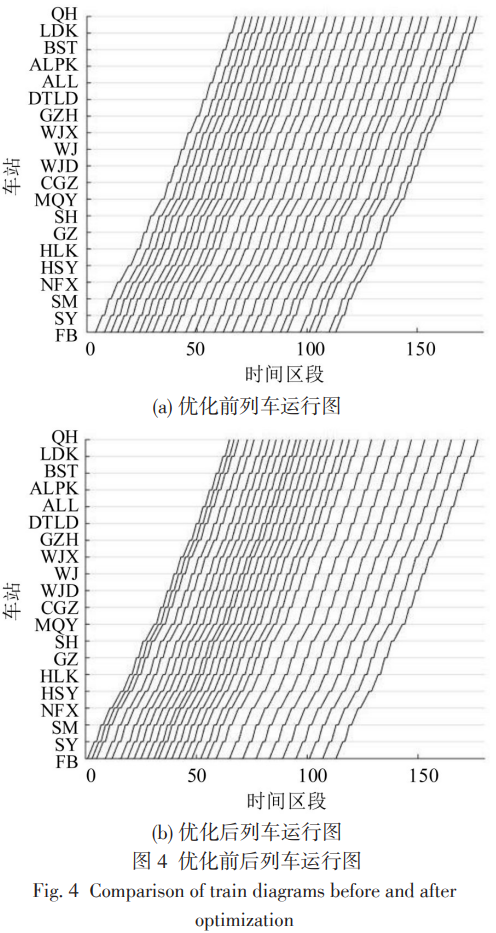
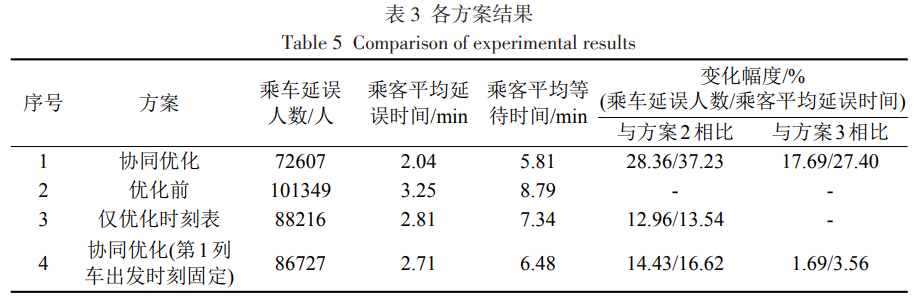
经过62.42 min 计算得出Gap为0.99%的近似最优解，其中乘车延误人数为72607人，列车运行图如图4(b)所示。可以看出，第 1~20 列车的发车间隔较小，均为2，3，4 min。优化前的方案为方案2，在该方案中列车时刻表采取实际运营时刻表，如图4(a)所示。不施加客流控制策略，记为方案3。在进行协同优化时将第1列车的发车时刻设置为固定值，记为方案4。其结果如下表所示。

小结

为缓解城市轨道交通车站拥挤情况，作者提出一种考虑换入客流影响的列车时刻表与客流控制协同优化方法，以最小化乘车延误人数为目标，通过将列车运行过程及乘客出行过程进行耦合并转化为相应的状态约束，构建了协同优化模型。利用优化求解器 CPLEX 调用分支定界法进行快速求解。该方法有效地降低了轨道交通线路各车站的乘车延误人数、乘客平均延误时间、乘客平均等待时间。