题目链接

Python3
直觉解法
class Solution:def strStr(self, haystack: str, needle: str) -> int:pn, ph = 0, 0n = len(needle) h = len(haystack)while ph < h:if haystack[ph] == needle[pn]:if pn == n-1: # 1234 123return ph - len(needle) + 1else: pn += 1ph += 1else: ## 1234 122ph = ph - pn + 1pn = 0return -1
方法一: 暴力解法 ⟮ O ( n × m ) 、 O ( 1 ) ⟯ \lgroup O(n\times m)、O(1) \rgroup ⟮O(n×m)、O(1)⟯
class Solution:def strStr(self, haystack: str, needle: str) -> int:for i in range(0, len(haystack)-len(needle)+1):if haystack[i:i+len(needle)] == needle:return i return -1

⭐ 方法二:Knuth-Morris-Pratt 算法 [KMP算法] ⟮ O ( m + n ) 、 O ( m ) ⟯ \lgroup O(m+n)、O(m) \rgroup ⟮O(m+n)、O(m)⟯ 【空间换时间】
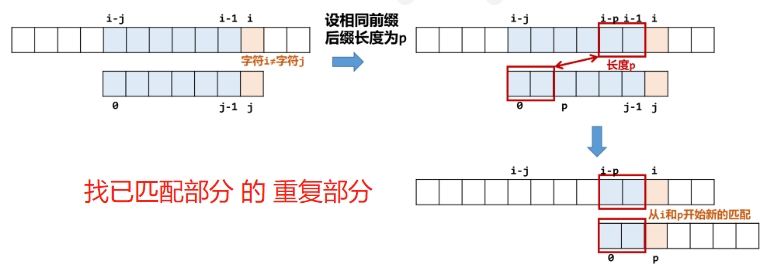

从而实现 更快地 跳转

参考链接1
参考链接2: KMP字符串匹配算法2
官方解法链接
class Solution:def strStr(self, haystack: str, needle: str) -> int:h = len(haystack)n = len(needle)# 获取 needle 的前缀信息lis = [0] * n j = 0 # 前后 子串长度for i in range(1, n): # 需要前后比较, 1个字符无法比较,因此从 i=1 开始while j > 0 and needle[i] != needle[j]: j = lis[j-1] # 和之前 相等的长度一样if needle[i] == needle[j]:j += 1 lis[i] = j # 0 1 2 3 4 5 6# a a b a a a b needle# 0 1 0 1 2 2 3 前缀子串 后缀子串 相同的长度 若是 needle[j] 不匹配了,注意是 lis[j-1] 存储的才是 待比较的下一个 j# a a c a a# 根据上述的 信息进行 匹配j = 0 # 遍历 needle 下标for i in range(0, h): # 遍历 haystack 下标while j > 0 and haystack[i] != needle[j]: # j = lis[j-1] # 这里 根据 前后缀 信息 快速跳转 if haystack[i] == needle[j]:j += 1if j == n: # needle 已全部匹配 因为前面的if 成立,j多加了1 return i - n + 1return -1 
链接
class Solution:def strStr(self, haystack: str, needle: str) -> int:def get_next():for i in range(1, len(needle)):k = fπ[i-1]while needle[i] != needle[k]:if k == 0:k -= 1break else:k = fπ[k-1]fπ[i] = k+1n = len(needle)fπ = [0] * n get_next() # 生成 needle 的next 数组i = 0 j = 0 while i < len(haystack):if haystack[i] == needle[j]:i += 1j += 1elif j == 0:i += 1else:j = fπ[j-1]if j >= n:return i - n return -1C++
KMP 算法 ⟮ O ( h + n ) 、 O ( n ) ⟯ \lgroup O(h+n)、O(n) \rgroup ⟮O(h+n)、O(n)⟯
class Solution {
public:int strStr(string haystack, string needle) {int h = haystack.size(), n = needle.size();vector<int> lis(n);for (int i = 1, j = 0; i < n; ++i){while (j > 0 && needle[i] != needle[j]){j = lis[j-1];}if (needle[i] == needle[j]){++j;}lis[i] = j;}for (int i = 0, j = 0; i < h; ++i){while (j > 0 && haystack[i] != needle[j]){j = lis[j-1];}if (haystack[i] == needle[j]){++j;}if (j == n){return i - n + 1;}}return -1;}
};
暴力解法
class Solution {
public:int strStr(string haystack, string needle) {int h = haystack.size(), n = needle.size();int j = 0, i = 0;while (i < h){if (haystack[i] == needle[j]){if (j == n-1){return i - n + 1;}else{++j;++i;}}else{j = 0;i = i - j + 1;}}return -1;}
};














——Thread类及常见方法(上篇))




