递归调用:一个函数,调用了自身,称为递归调用
递归函数:一个会调用自身的函数
凡是循环能做的事,递归都能做。
目录
递归示例
普通方法实现
递归方式实现
计算分析:
递归遍历目录
引入os
遍历目录
执行结果
模拟栈结构
压栈
出栈
模拟栈遍历目录(深度)
图解
引入os
遍历目录
执行结果
队列
引入类库
创建队列
进队
出队
队列遍历目录(广度)
图解
引入类库
遍历目录
执行结果
总结
递归示例
输入一个整数,求1+2+3+......+n的和
普通方法实现
使用for循环方式,在循环中累加计算总和。
示例如下:
def sum1(n):""" 普通方法实现求n相加之和 """sum = 0for x in range(1, n + 1):sum += xreturn sumprint(sum1(100))
# 执行结果
# 5050递归方式实现
需要改换方式,通过反复调用同一个方法也就是本身来实现数字总和计算。
计算分析:
sum2(0) = 0
sum2(1) = 1
sum2(2) = 2 + sum2(1)
sum2(3) = 3 + sum2(2)
sum2(4) = 4 + sum2(3)
示例如下:
def sum2(n):"""递归方法实现求n相加之和 """if n in (0, 1):return nelse:return n + sum2(n - 1)print(sum2(100))
# 执行结果
# 5050递归遍历目录
引入os
示例如下:
import os遍历目录
使用os函数去检索和判断目录和文件进行分别处理。
示例如下:
def get_all_dir(path, space=''):# 得到当前目录下所有的文件列表dirs = os.listdir(path)space += '--'for fileName in dirs:# 判断是否是目录(绝对路径)abdPath = os.path.join(path, fileName)if os.path.isdir(abdPath):print(space + '目录:', fileName)# 递归调用get_all_dir(abdPath, space)else:print(space + '普通文件:', fileName)get_all_dir(r'E:\lianxipy\huahua')执行结果
--普通文件: aixin.py
--普通文件: aixin2.py
--普通文件: demo.py
--普通文件: dog.py
--普通文件: dongwu.py
--目录: img
----普通文件: duolai.jpg
----普通文件: duolai2.png
----普通文件: lianhua.jpg
----普通文件: qie.jpg
----普通文件: qie2.jpg
----普通文件: tiaowa.png
----普通文件: tiaowa2.jpg
----普通文件: tiaowa3.jpg
----普通文件: tree.jpg
----普通文件: VCG211171443872.jpg
----普通文件: VCG211171443874.jpg
----普通文件: VCG41N1156862653.jpg
----普通文件: VCG41N1255524799.jpg
----普通文件: VCG41N689213498.jpg
----普通文件: VCG41N882899088.jpg
--普通文件: min_yellow.py
--普通文件: shu.py
--普通文件: tree.py
--普通文件: wuhuan.py
--普通文件: yu.py模拟栈结构
下面将模拟栈结构向其中添加数据,在做出栈操作(先入后出)。
压栈
设定栈变量,并通过append方法每次向其中添加一个名称数据。
示例如下:
stack = []# 压栈(向其中添数据)
stack.append('zhangsan')
print(stack)
stack.append('lisi')
print(stack)
stack.append('wangwu')
print(stack)# 执行结果
# ['zhangsan']
# ['zhangsan', 'lisi']
# ['zhangsan', 'lisi', 'wangwu']出栈
通过pop方法每次出栈一个数据,出栈方式为:先入后出。
示例如下:
print('出栈:', stack.pop())
print('出栈:', stack.pop())
print('出栈:', stack.pop())
print('结果:', stack)# 执行结果
# 出栈: wangwu
# 出栈: lisi
# 出栈: zhangsan
# 结果: []模拟栈遍历目录(深度)
图解
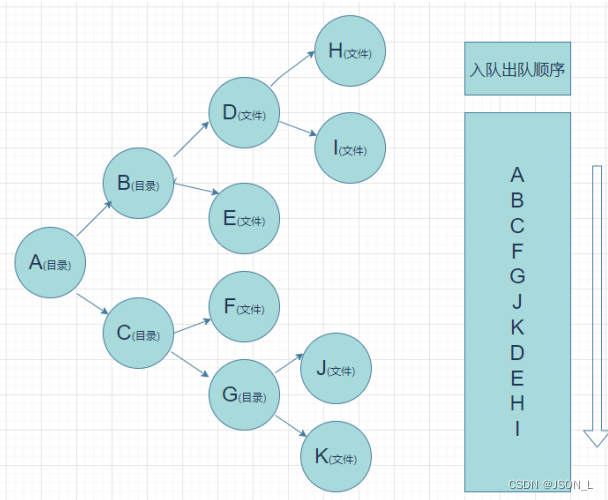
引入os
示例如下:
import os遍历目录
示例如下:
def get_all_dir_stack(path):stack = []stack.append(path)# 处理栈, 当栈为空的时候结束训话while len(stack) != 0:# 从站里取出数据dirPath = stack.pop()files = os.listdir(dirPath)# 处理每一个文件,如果普通文件就打印# 如果是一个目录就将该目录压栈for fileName in files:absPath = os.path.join(dirPath, fileName)if os.path.isdir(absPath):print('目录:', fileName)stack.append(absPath)else:print('普通文件:', fileName)get_all_dir_stack(r'E:\lianxipy\huahua')执行结果
普通文件: aixin.py
普通文件: aixin2.py
普通文件: demo.py
普通文件: dog.py
普通文件: dongwu.py
目录: img
普通文件: min_yellow.py
普通文件: shu.py
普通文件: tree.py
普通文件: wuhuan.py
普通文件: yu.py
普通文件: duolai.jpg
普通文件: duolai2.png
普通文件: lianhua.jpg
普通文件: qie.jpg
普通文件: qie2.jpg
普通文件: tiaowa.png
普通文件: tiaowa2.jpg
普通文件: tiaowa3.jpg
普通文件: tree.jpg
普通文件: VCG211171443872.jpg
普通文件: VCG211171443874.jpg
普通文件: VCG41N1156862653.jpg
普通文件: VCG41N1255524799.jpg
普通文件: VCG41N689213498.jpg
普通文件: VCG41N882899088.jpg队列
引入类库
创建队列需要引入类库来实现。
示例如下:
import collections创建队列
调用collections的deque方法来创建一个队列。
示例如下:
queue = collections.deque()
print(queue)# 执行结果
# deque([])进队
向队列中加入三个人员名称,最后可看到队列中增加了三个数据。
示例如下:
queue.append('zhangsan')
print(queue)
queue.append('lisi')
print(queue)
queue.append('wangwu')
print(queue)# 执行结果
# deque(['zhangsan'])
# deque(['zhangsan', 'lisi'])
# deque(['zhangsan', 'lisi', 'wangwu'])出队
使用popleft方法将队列中的数据一个个的出队。
示例如下:
print('出队:', queue.popleft())
print('出队:', queue.popleft())
print('出队:', queue.popleft())
print('结果:', queue)# 执行结果
# 出队: zhangsan
# 出队: lisi
# 出队: wangwu
# 结果: deque([])队列遍历目录(广度)
图解
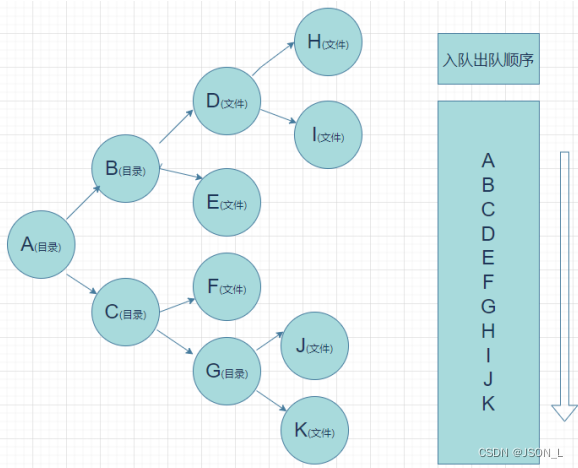
引入类库
引入类库os和队列使用的collections。
示例如下:
import os
import collections遍历目录
示例如下:
def get_all_dir_queue(path):# 创建队列queue = collections.deque()# 进队queue.append(path)while len(queue) != 0:# 出队数据dirPath = queue.popleft()# 找出所有的文件dirs = os.listdir(dirPath)for fileName in dirs:# 绝对路径absPath = os.path.join(dirPath, fileName)# 判断是否目录,是目录就进队,不是就打印if os.path.isdir(absPath):print('目录:', fileName)queue.append(absPath)else:print('普通文件:', fileName)get_all_dir_queue(r'E:\lianxipy\huahua')执行结果
普通文件: aixin.py
普通文件: aixin2.py
普通文件: demo.py
普通文件: dog.py
普通文件: dongwu.py
目录: img
普通文件: min_yellow.py
普通文件: shu.py
普通文件: tree.py
普通文件: wuhuan.py
普通文件: yu.py
普通文件: duolai.jpg
普通文件: duolai2.png
普通文件: lianhua.jpg
普通文件: qie.jpg
普通文件: qie2.jpg
普通文件: tiaowa.png
普通文件: tiaowa2.jpg
普通文件: tiaowa3.jpg
普通文件: tree.jpg
普通文件: VCG211171443872.jpg
普通文件: VCG211171443874.jpg
普通文件: VCG41N1156862653.jpg
普通文件: VCG41N1255524799.jpg
普通文件: VCG41N689213498.jpg
普通文件: VCG41N882899088.jpg总结
本篇主要是递归介绍、计算数字总和、遍历目录及模拟栈、队列应用和遍历目录。





并 实现文件传输且反馈)

)











