文章目录
- Reinfocement Learning
- 一、基本概念
- 二、贝尔曼公式(bellman equation)
- 2.1 为什么return重要
- 2.2 state value function的定义
- 2.3 贝尔曼公式推导
- 2.4 如何求解贝尔曼公式
- 2.5 Action value的定义
- 三、贝尔曼最优公式(bellman optimality equation)
- 3.1 最优策略和公式推导
- 3.2 公式求解
- 3.3 最优策略的有趣性质
- 四、值迭代和策略迭代(Value Iteration & Policy Iteration)
- 4.1 值迭代算法
- 4.2 策略迭代算法
- 4.3 二者区别
- 4.4 截断策略迭代算法(Truncated Policy Iteration)
- 五、蒙特卡洛方法(Monte Carlo Learning)
- 5.1 有模型与免模型强化学习
- 5.2 MC Basic算法
- 5.3 MC Exploring Starts算法
- 5.4 MC Epsilon-Greedy算法
Reinfocement Learning
一、基本概念
-
强化学习(Reinfocement Learning):智能体(agent)可以在与复杂且不确定的环境进行交互时,尝试使所获得的奖励最大化的算法(寻找最优策略)。
-
动作(action):环境接收到的智能体基于当前状态的输出,即智能体采取什么动作。
-
状态(state):智能体从环境中获取的状态。
-
状态转移(state transition):采取动作,智能体从一个状态转变到另一个状态。
-
策略(policy):对每个状态而言,智能体会用策略来选取下一步的动作。
-
随机性策略(stochastic policy): π \pi π 函数,即 π ( a ∣ s ) = p ( a t = a ∣ s t = s ) \pi(a|s)=p(a_t=a|s_t =s) π(a∣s)=p(at=a∣st=s)。输入一个状态 s s s,输出一个概率。
-
确定性策略(deterministic policy):智能体直接采取最有可能的动作。
-
-
奖励(reward):智能体从环境中获取的反馈信号,这个信号指定了智能体在某一步采取了某个策略以后是否得到奖励,以及奖励的大小。
-
轨迹(trajectory):状态—动作—奖励链
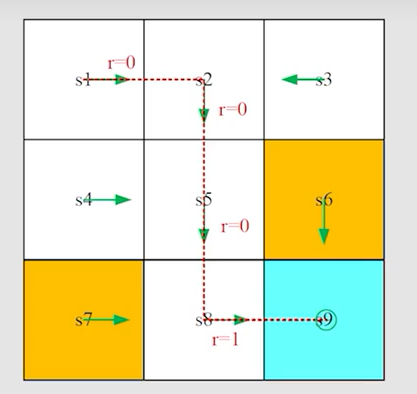
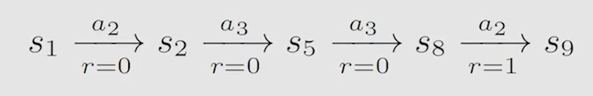
-
回报(return):奖励的逐步叠加。如上述 t r a j e c t o r y trajectory trajectory 的 r e t u r n return return 为 0 + 0 + 0 + 1 = 1 0+0+0+1=1 0+0+0+1=1
-
折扣回报(discounted return):引入了一个折扣因子(discounted rate) γ \gamma γ,则折扣回报 G t G_t Gt为:
G t = r t + 1 + γ r t + 2 + γ 2 r t + 3 + γ 3 r t + 4 + . . . γ T − t + 1 r T G_t=r_{t+1}+\gamma r_{t+2}+\gamma^2 r_{t+3}+\gamma^3 r_{t+4}+...\gamma^{T-t+1}r_T Gt=rt+1+γrt+2+γ2rt+3+γ3rt+4+...γT−t+1rT-
有些马尔可夫过程带环,它并不会终结,我们想避免无穷的奖励
-
把折扣因子设为0,我们就只关注当前的奖励;把折扣因子设为1,对未来的奖励并没有打折扣,未来获得的奖励与当前获得的奖励是一样的
-
-
episode:agent在环境里面执行某个策略从开始到结束(到达terminal state)这一过程。
-
马尔可夫决策过程(Markov decision process, MDP)
key elements of MDP:
-
集合(sets)
- state:状态的集合 S S S
- action:动作的集合 A ( s ) A(s) A(s),即在状态 s s s 下,智能体可采取的动作有哪些
- reward:奖励的集合 R ( s , a ) R(s, a) R(s,a),即在当前状态 s s s 下,采取动作 a a a 将会获得多少奖励
-
概率分布(probabiliy distribution)
- state transition probability:在状态 s s s 下,采取动作 a a a,转移到下一状态 s ′ s' s′ 的概率,即 p ( s ′ ∣ s , a ) p(s'|s,a) p(s′∣s,a)
- reward probability:在状态 s s s 下,采取动作 a a a,获得奖励 r r r 的概率,即 p ( r ∣ s , a ) p(r|s,a) p(r∣s,a)
-
策略(policy):在状态 s s s 下,采取动作 a a a 的概率,即 π ( a ∣ s ) \pi(a|s) π(a∣s)
-
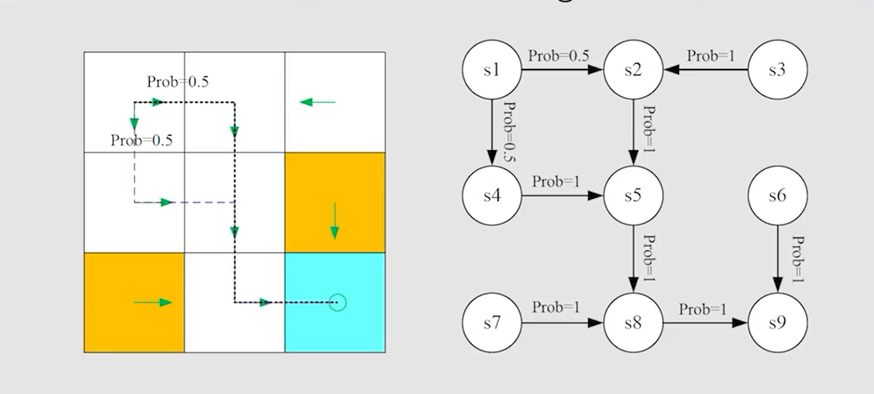
马尔可夫性质(Markov property):memoryless property,下一状态和奖励只跟当前状态和采取的动作有关,跟之前所有的都无关。
p ( s t + 1 ∣ a t + 1 , s t , . . . , a 1 , s 0 ) = p ( s t + 1 ∣ a t + 1 , s t ) p ( r t + 1 ∣ a t + 1 , s t , . . . , a 1 , s 0 ) = p ( r t + 1 ∣ a t + 1 , s t ) p(s_{t+1}|a_{t+1},s_t,...,a_1,s_0)=p(s_{t+1}|a_{t+1},s_t) \\ p(r_{t+1}|a_{t+1},s_t,...,a_1,s_0)=p(r_{t+1}|a_{t+1},s_t) p(st+1∣at+1,st,...,a1,s0)=p(st+1∣at+1,st)p(rt+1∣at+1,st,...,a1,s0)=p(rt+1∣at+1,st)
-
如图为一个markov process,而不是markov decision process,因为policy已经确定
二、贝尔曼公式(bellman equation)
2.1 为什么return重要
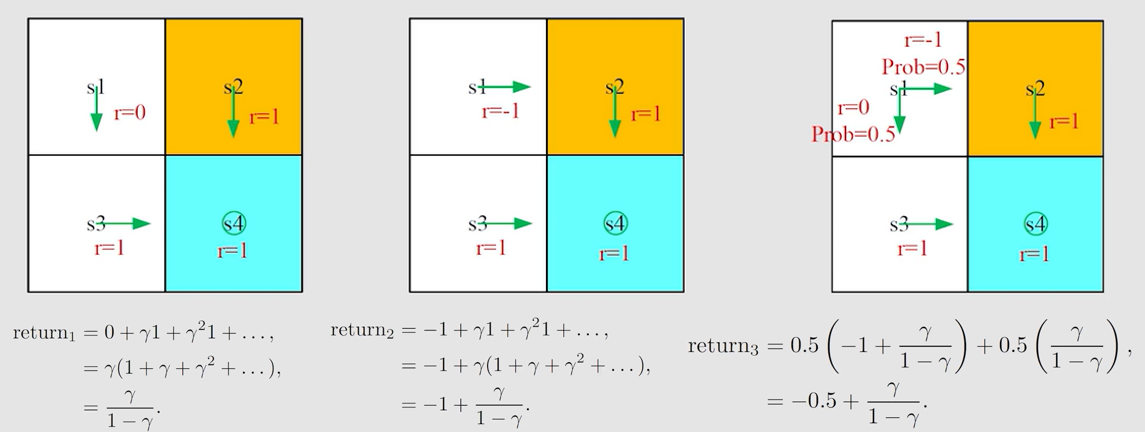
r e t u r n return return 可作为评估策略好坏的依据。
由图可知, r e t u r n 1 > r e t u r n 3 > r e t u r n 2 return_1>return_3>return_2 return1>return3>return2,故策略1是最好的,策略2是最差的。
2.2 state value function的定义
折扣回报(discounted return):
G t = r t + 1 + γ r t + 2 + γ 2 r t + 3 + γ 3 r t + 4 + . . . γ T − t + 1 r T G_t=r_{t+1}+\gamma r_{t+2}+\gamma^2 r_{t+3}+\gamma^3 r_{t+4}+...\gamma^{T-t+1}r_T Gt=rt+1+γrt+2+γ2rt+3+γ3rt+4+...γT−t+1rT
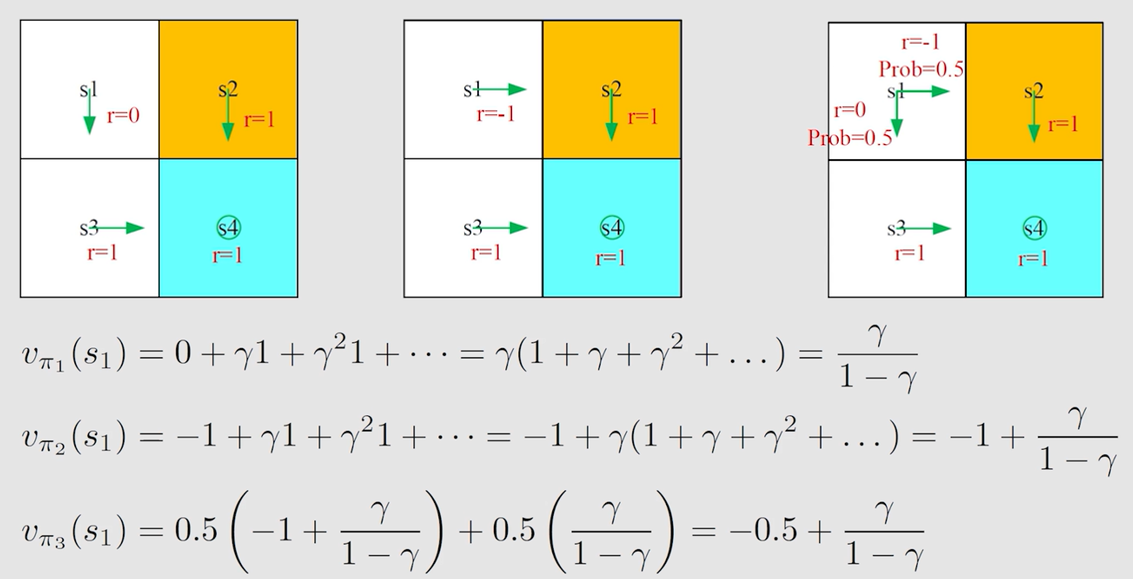
s t a t e v a l u e f u n c t i o n state \ value \ function state value function 就是折扣回报(discounted return)的期望。即从一个状态出发,agent能获得的折扣回报的期望:
v π ( s ) = E [ G t ∣ S t = s ] v_\pi(s)=\mathbb{E}[G_t|S_t=s] vπ(s)=E[Gt∣St=s]
-
这是关于状态 s s s 的函数,从不同的状态出发,得到的 t r a j e c t o r y trajectory trajectory 是不同的, d i s c o u n t e d r e t u r n discounted\ return discounted return 的期望也是不同的
-
这是基于策略 π \pi π 的函数,采取不同的策略,得到的 t r a j e c t o r y trajectory trajectory 是不同的, d i s c o u n t e d r e t u r n discounted\ return discounted return 的期望也是不同的
-
当一个 s t a t e v a l u e f u n c t i o n state \ value \ function state value function 比较大时,代表这个状态是比较有价值的,因为从这个状态出发会得到更多的 r e t u r n return return
-
r e t u r n return return 是由一条确定 t r a j e c t o r y trajectory trajectory 得到的,而 s t a t e v a l u e state \ value state value 是从当前状态出发,可能会得到多条 t r a j e c t o r y trajectory trajectory,对其 r e t u r n return return 求平均
2.3 贝尔曼公式推导
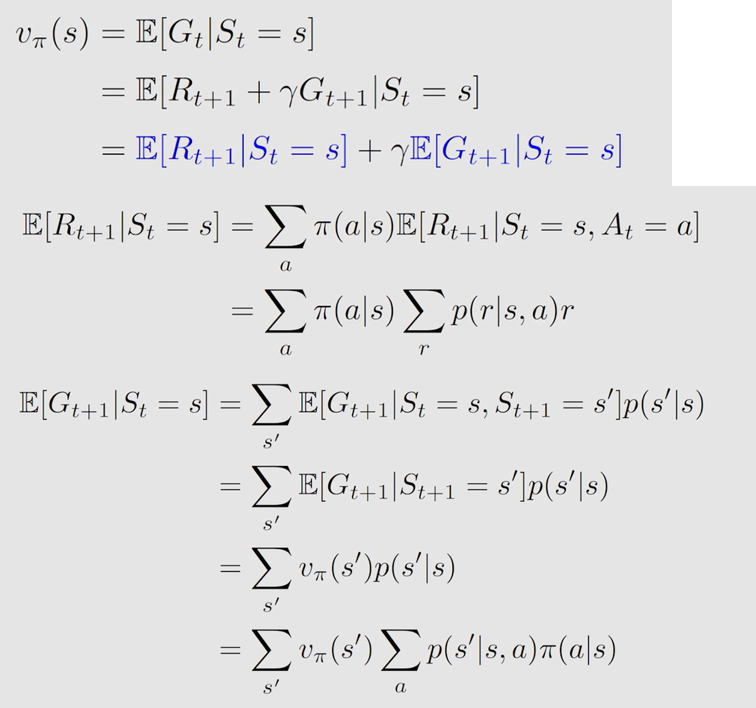
E [ R t + 1 ∣ S t = s ] \mathbb{E}[R_{t+1}|S_t=s] E[Rt+1∣St=s] 表示的是当前奖励的平均, E [ G t + 1 ∣ S t = s ] \mathbb{E}[G_{t+1}|S_t=s] E[Gt+1∣St=s] 表示下一回报的平均
由此可得贝尔曼公式:
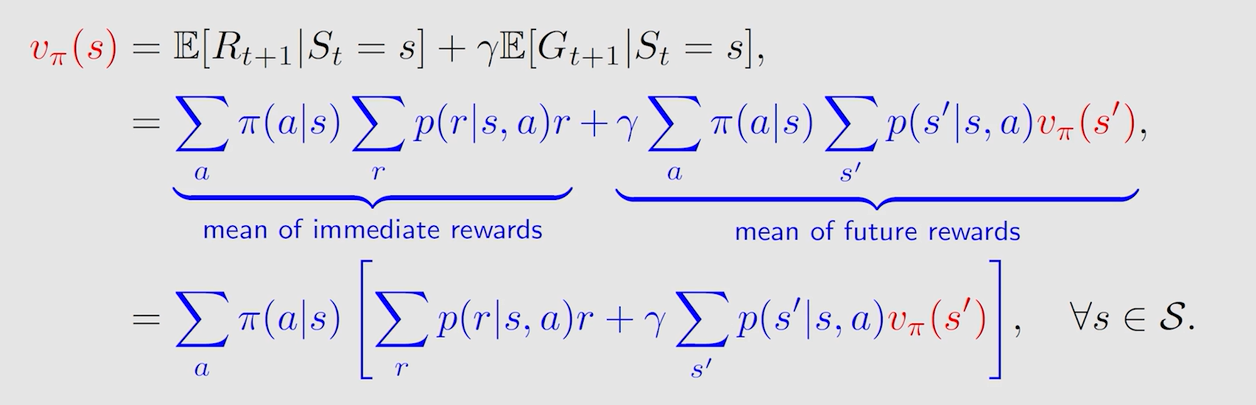
- 贝尔曼公式就是 s t a t e v a l u e state \ value state value(的表现形式)
- 贝尔曼公式描述了不同 s t a t e v a l u e state \ value state value 之间的关系
- 对于状态空间中的所有状态均成立
- 贝尔曼公式依赖于给定的策略 π \pi π,这样才能求解
- 计算状态价值函数的过程就是策略评估( p o l i c y e v a l u a t i o n policy \ evaluation policy evaluation)
- 其实直观上是非常好理解的,因为 G t = r t + 1 + γ r t + 2 + γ 2 r t + 3 + γ 3 r t + 4 + . . . γ T − t + 1 r T = r t + 1 + γ G t + 1 G_t=r_{t+1}+\gamma r_{t+2}+\gamma^2 r_{t+3}+\gamma^3 r_{t+4}+...\gamma^{T-t+1}r_T = r_{t+1}+\gamma G_{t+1} Gt=rt+1+γrt+2+γ2rt+3+γ3rt+4+...γT−t+1rT=rt+1+γGt+1,我要求 G t G_t Gt 的期望,其实就是求即刻奖励的期望和下一折扣回报的期望。
2.4 如何求解贝尔曼公式
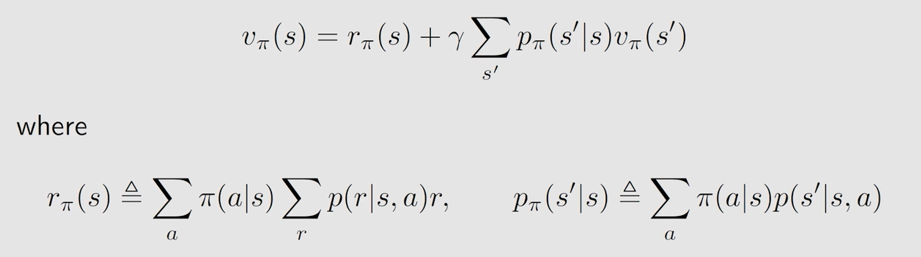
对于 n n n 个状态而言:
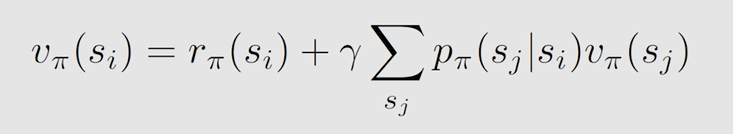
用矩阵形式表示(假设共有四个状态):
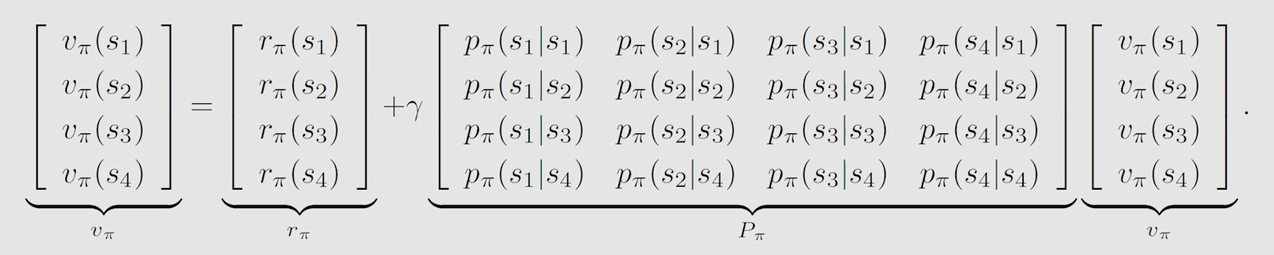
例子:
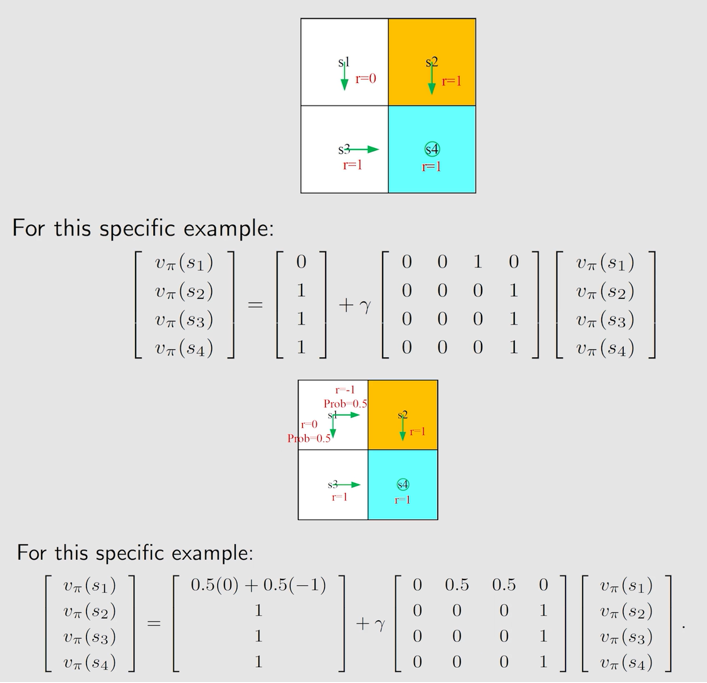
2.5 Action value的定义
s t a t e v a l u e state \ value state value 关注的是从一个状态出发, a g e n t agent agent 能获得的折扣回报的期望。它体现了每个状态的价值。
a c t i o n v a l u e action \ value action value 关注的是从状态出发,采取某个 a c t i o n action action 能获得的折扣回报的期望。它体现了每个动作的价值。有如下数学定义:
q π ( s , a ) = E [ G t ∣ S t = s , A t = a ] q_\pi(s,a)=\mathbb{E}[G_t|S_t=s,A_t=a] qπ(s,a)=E[Gt∣St=s,At=a]
两者可以互相求解:
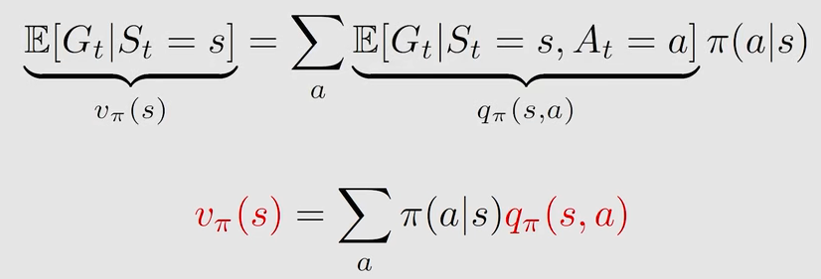
因此(上图有推导):
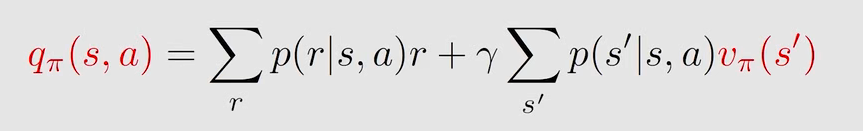
三、贝尔曼最优公式(bellman optimality equation)
3.1 最优策略和公式推导
最优策略:当一个策略 π ∗ \pi^* π∗ 的所有状态对应的 s t a t e v a l u e state \ value state value 值都大于其他任何一个策略时,即 $v_\pi^*(s)>v_\pi(s) $ 时,称 π ∗ \pi^* π∗ 是最优策略。
贝尔曼最优公式,就是当贝尔曼公式中的策略不再给定,而是要求解采用什么策略是最优的一个过程,知道了最优策略过后,当然可以求出最优的 s t a t e v a l u e state \ value state value。贝尔曼最优公式就是当给定的策略为最优策略时的一个特殊的贝尔曼公式:
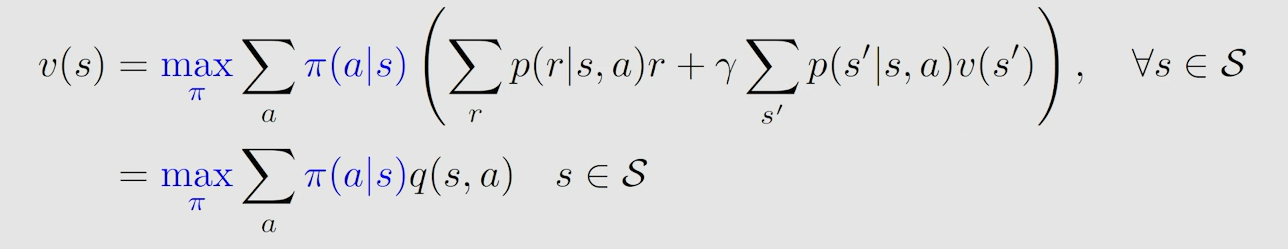
假设所有 q ( s , a ) q(s,a) q(s,a) 已知时,一定存在一个最大的 q ( s , a ) q(s,a) q(s,a) ,我们想让 v ( s ) v(s) v(s) 最大,那就是让最大的 q ( s , a ) q(s,a) q(s,a) 所占的权重最大,而权重代表概率,最大为1。所以采取的策略就是让 a c t i o n v a l u e action \ value action value 最大的 a c t i o n action action 发生概率为1,此时得到的 s t a t e v a l u e state \ value state value 值即为 a c t i o n v a l u e action \ value action value。
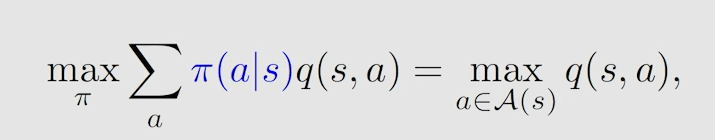
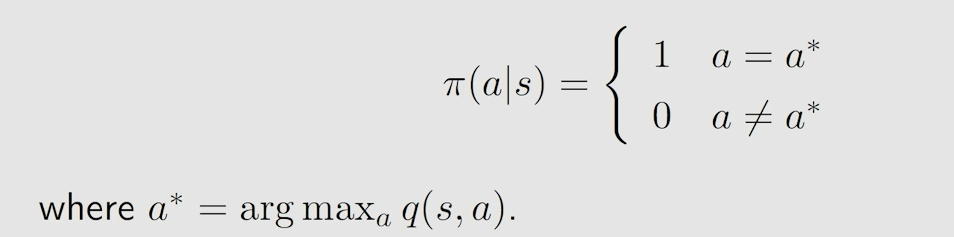
以矩阵形式表示为:
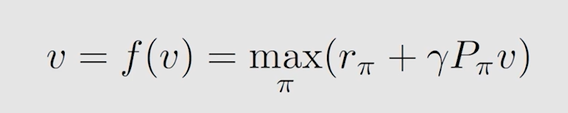
3.2 公式求解
基于 c o n t r a c t i o n m a p p i n g t h e o r e m contraction \ mapping \ theorem contraction mapping theorem:
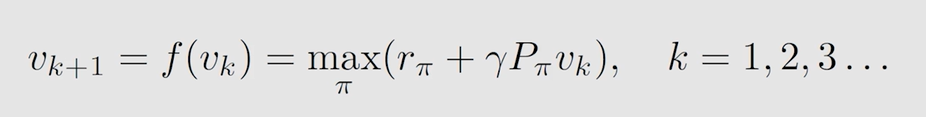
- 对任意状态 s s s,都先给出一个估计值 v k ( s ) v_k(s) vk(s) ( k k k 表示迭代次数)
- 根据 a c t i o n v a l u e action \ value action value 公式可以求解出 q k ( s , a ) q_k(s,a) qk(s,a)
- 根据 m a x max max 可以求解出 q k ( s , a ) q_k(s,a) qk(s,a) 对应的策略 π \pi π(就是选择最大的 q k ( s , a ) q_k(s,a) qk(s,a) 的策略,此时得到当前的最优策略 π ∗ \pi^* π∗)
- 将 m a x a q k ( s , a ) max_{a} \ q_k(s,a) maxa qk(s,a) 的值计算出来带入 v k + 1 ( s ) v_{k+1}(s) vk+1(s)
- 不断迭代至 v ∗ v^* v∗ 收敛(即 v k ( s ) v_k(s) vk(s) 与 v k + 1 ( s ) v_{k+1}(s) vk+1(s) 的差值很小时)
例子:
表格中存储的是 a c t i o n v a l u e action \ value action value,此表即为 Q − t a b l e Q-table Q−table

第一轮迭代 k = 0 k=0 k=0,假设 v 0 ( s 1 ) = v 0 ( s 2 ) = v 0 ( s 3 ) = 0 v_0(s_1)=v_0(s_2)=v_0(s_3)=0 v0(s1)=v0(s2)=v0(s3)=0(下标0表示迭代次数 k k k),可得表格:
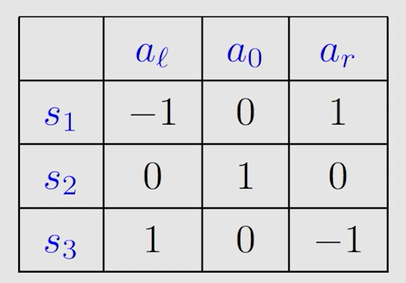
由表得到第一轮迭代的最优策略和最优 s t a t e v a l u e state \ value state value :
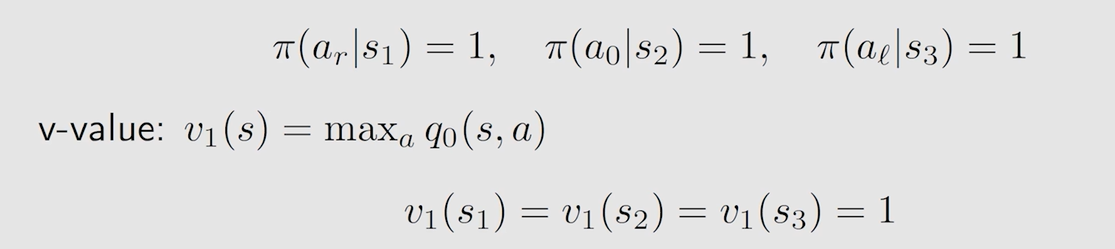
第二轮迭代 k = 1 k=1 k=1,将第一轮的最优 s t a t e v a l u e state \ value state value 带入得到新的表格:
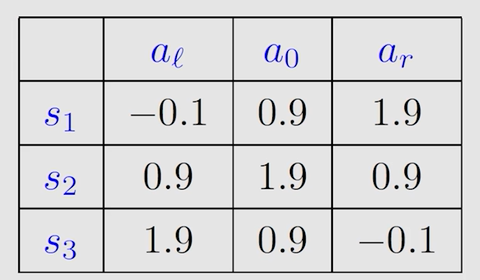
由表得到第二轮迭代的最优策略和最优 s t a t e v a l u e state \ value state value :
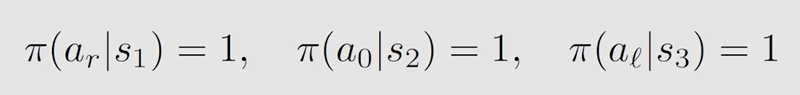
不断迭代下去,直到第 k k k 轮的 v ∗ v^* v∗ 收敛可停止迭代,得到最终的最优策略和最优 s t a t e v a l u e state \ value state value。
3.3 最优策略的有趣性质
影响最优策略的因素:奖励 r e w a r d reward reward 和折扣因子 γ \gamma γ 会影响到最优策略
当奖励发生线性变化时,最优策略并不会改变
Q Q Q:为了寻找最短路径,防止绕远路有必要将每走一步的 r e w a r d reward reward 设置为负数吗? A A A:没有必要,因为不仅是 r e w a r d reward reward 限制,折扣因子也会限制,绕远路意味着拿到奖励会打折的非常厉害,为了获取最大 s t a t e v a l u e state \ value state value 肯定选近路。
贝尔曼最优公式一定存在解,且解唯一(最优策略不唯一,最优 s t a t e v a l u e state \ value state value 唯一)
四、值迭代和策略迭代(Value Iteration & Policy Iteration)
二者都属于 d y n a m i c p r o g r a m m i n g dynamic \ programming dynamic programming 的方法(或者说是 m o d e l − b a s e d model-based model−based 的方法)
4.1 值迭代算法
其实就是贝尔曼最优公式的求解过程。
s t e p 1 : p o l i c y u p d a t e step1:policy \ update step1:policy update
由前面的贝尔曼最优公式可知,最优策略的数学表示为:
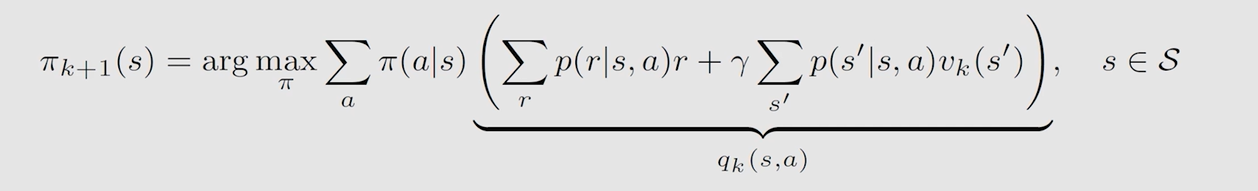
a r g m a x a f ( a ) arg \ \underset {a}{max}f(a) arg amaxf(a) 表示 f ( a ) f(a) f(a) 取最大时 a a a 的值。故上述式子的含义为后面这一长串(即 s t a t e v a l u e state \ value state value)取最大值时所采取的策略,即最优策略,表示为:


即采取的策略为选取对应 q k ( s , a ) q_k(s,a) qk(s,a) 最大的那个 a c t i o n action action,概率为1。
s t e p 2 : v a l u e u p d a t e step2:value \ update step2:value update
此时策略已定,贝尔曼最优公式转变为贝尔曼公式:
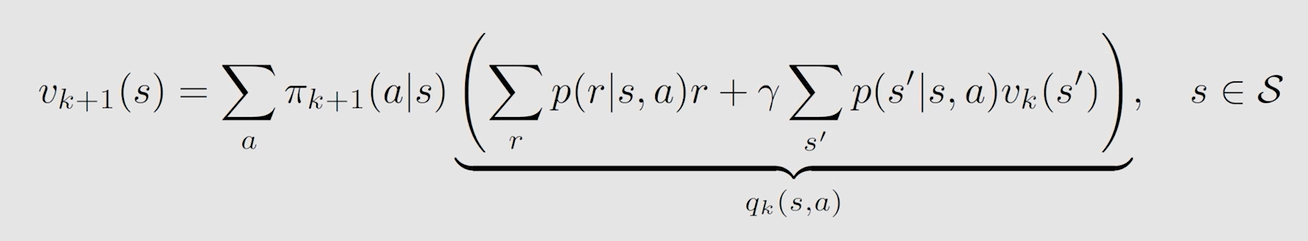
得到最优 s t a t e v a l u e state \ value state value,就是最大的 a c t i o n v a l u e action \ value action value,因为最优策略选取最大 a c t i o n v a l u e action \ value action value 对应 a c t i o n action action 的概率为1,所以只有一条 t r a j e c t o r y trajectory trajectory:
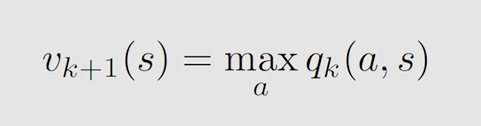
概括为先定 v k v_k vk 求 q k q_k qk 再求 π k + 1 \pi_{k+1} πk+1 最后得到 v k + 1 v_{k+1} vk+1,迭代至其收敛。
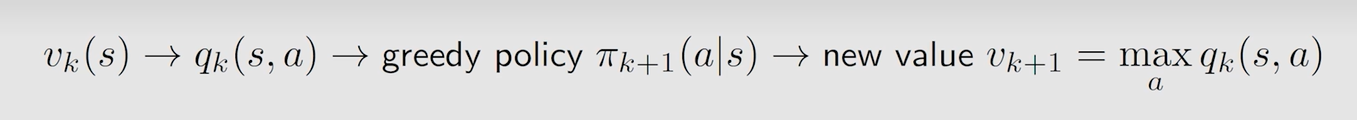
完整例子:
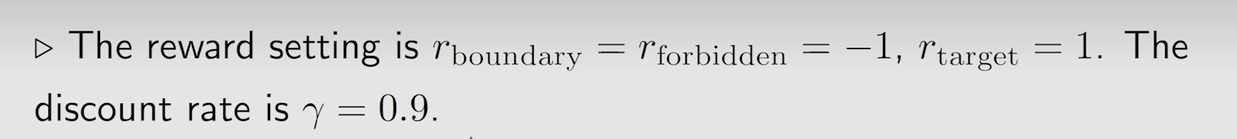
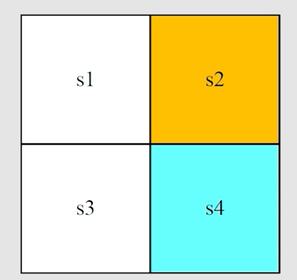
表格中存储的是 a c t i o n v a l u e action \ value action value,此表即为 Q − t a b l e Q-table Q−table

第一轮迭代:
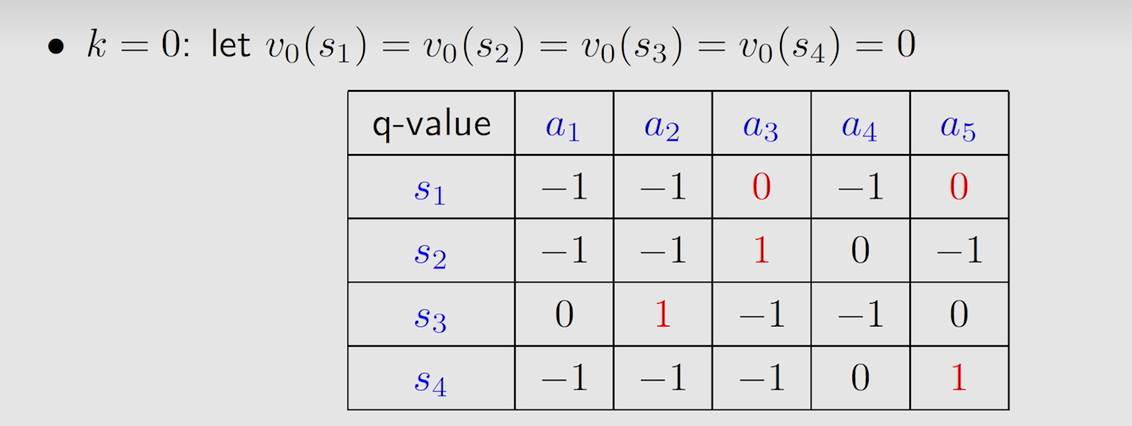
表中状态为 s 1 s_1 s1 时选的动作 a 3 a_3 a3 和 a 5 a_5 a5 得到的 a c t i o n v a l u e action \ value action value 值相同,此时随机选择一个,假设为 a 5 a_5 a5:
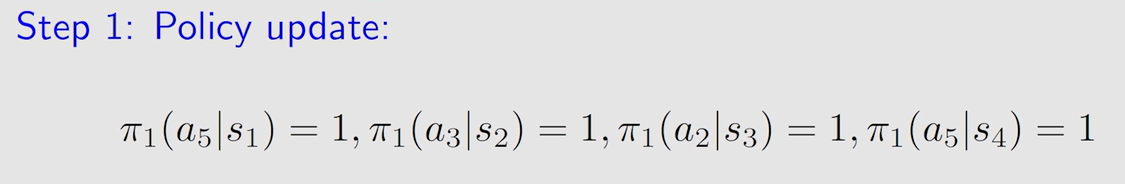
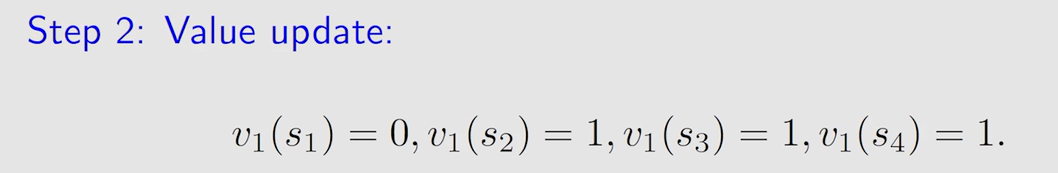
得到新的策略图:
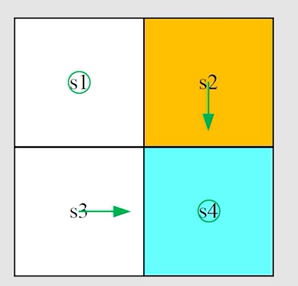
第二轮迭代:

得到新的策略图:
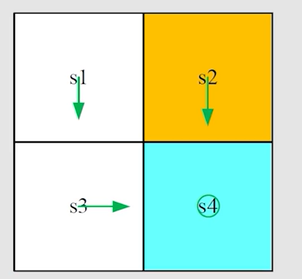
继续往下迭代,知道 ∣ ∣ v k − v k + 1 ∣ ∣ ||v_k-v_{k+1}|| ∣∣vk−vk+1∣∣ 很小时,即收敛到 v ∗ v^* v∗ 时停止。
4.2 策略迭代算法
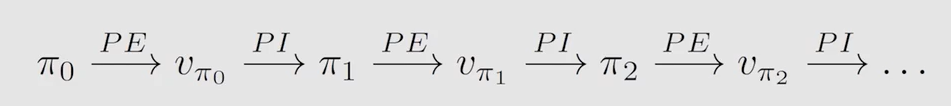
P E = P o l i c y E v a l u a t i o n PE=Policy \ Evaluation PE=Policy Evaluation, P I = P o l i c y I m p r o v e m e n t PI=Policy \ Improvement PI=Policy Improvement
s t e p 1 : p o l i c y e v a l u a t i o n step1:policy \ evaluation step1:policy evaluation
给定策略,求解贝尔曼方程,不断迭代 j j j 轮至 v π k v_{\pi_k} vπk 收敛:
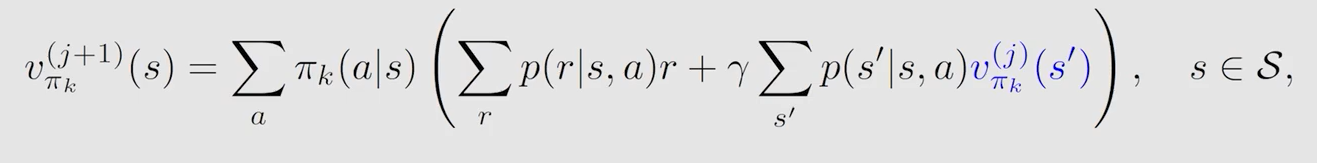
s t e p 2 : p o l i c y i m p r o v e m e n t step2:policy \ improvement step2:policy improvement
根据上一步得到的 s t a t e v a l u e state \ value state value 求解贝尔曼最优公式,更新策略:
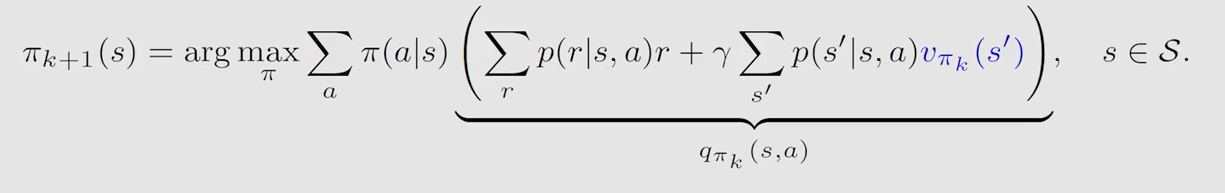
同值迭代一样,选取最大 a c t i o n v a l u e action \ value action value 对应 a c t i o n action action,使其概率为1更新策略:
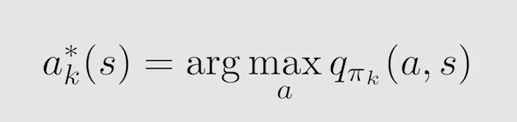
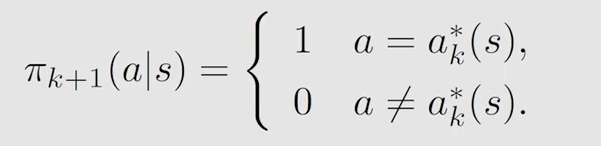
简单例子:
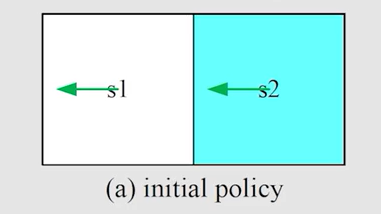
第一步策略评估,即求解贝尔曼公式:

因为例子比较简单,可以直接联系方程组解出:
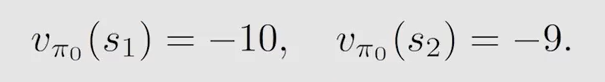
如果当式子较难解出,一般采用迭代的算法让其收敛,即当 v π k ( j + 1 ) v_{\pi_k}^{(j+1)} vπk(j+1) 与 v π k ( j ) v_{\pi_k}^{(j)} vπk(j) 差值很小时:
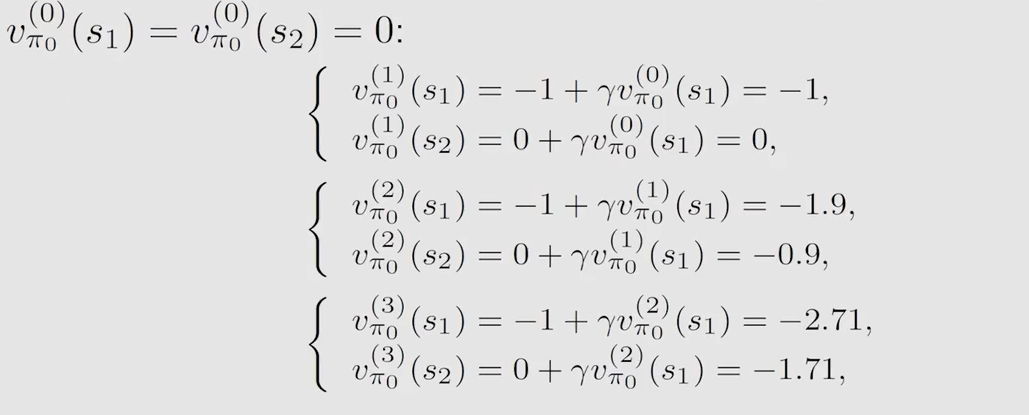
第二部策略优化,将上述得到的 s t a t e v a l u e state \ value state value 带入,此时就跟值迭代算法一样了:

得到新的策略:
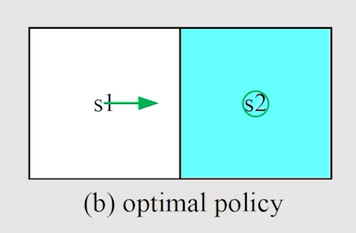
4.3 二者区别

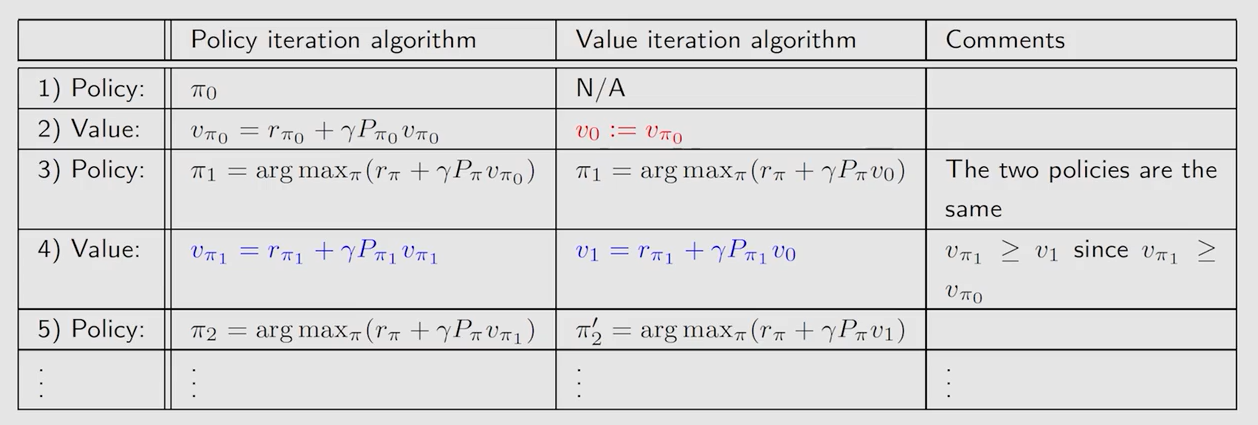
上图中当 v v v 的下标为 π \pi π 时,表示的是由确切的策略求解出的 s t a t e v a l u e state \ value state value;当 v v v 的下标为数字时,表示的只是迭代过程中的一个中间量,是用这个中间两来不断逼近真正的 s t a t e v a l u e state \ value state value,可以看作是未收敛的 s t a t e v a l u e state \ value state value。
策略迭代是由初始时给定的策略来计算出 s t a t e v a l u e state \ value state value,而值迭代是直接给出一个估计值,之后求解贝尔曼最优方程时的步骤时,策略迭代带入的是由确切的策略通过求解贝尔曼方程出的 s t a t e v a l u e state \ value state value,而值迭代带入的是未收敛的 s t a t e v a l u e state \ value state value。相当于在每一轮迭代开始前,策略迭代多了一步求 s t a t e v a l u e state \ value state value 的过程,这个过程也是一个迭代的过程。
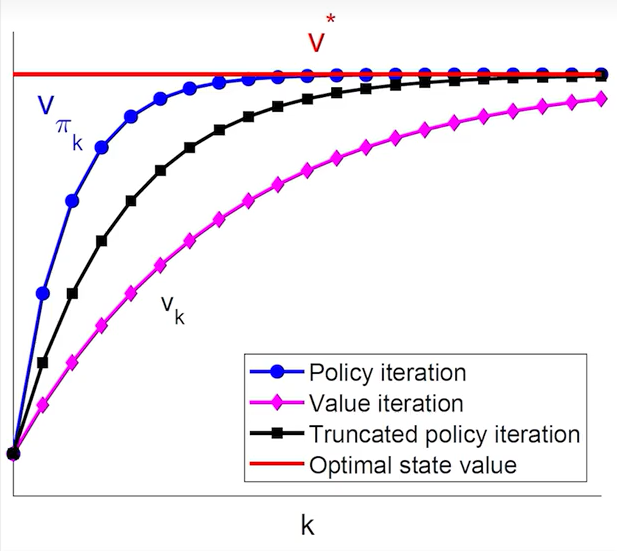
4.4 截断策略迭代算法(Truncated Policy Iteration)

五、蒙特卡洛方法(Monte Carlo Learning)
5.1 有模型与免模型强化学习
有模型(model-based)强化学习: a g e n t agent agent 通过学习状态的转移来采取动作。具体来说,当 a g e n t agent agent 知道状态转移函数和奖励函数(即 M D P MDP MDP 中的两个概率分布)后,它就能知道在某一状态下执行某一动作后能带来的奖励和环境的下一状态。
免模型(model-free)强化学习: a g e n t agent agent 没有直接去估计状态的转移,也没有得到环境的具体转移变量,它通过学习状态价值函数和策略函数进行决策。免模型强化学习没有对真实环境进行建模, a g e n t agent agent 只能在真实环境中通过一定的策略来执行动作,等待奖励和状态迁移,然后根据这些反馈信息来更新动作策略,反复迭代直到学习到最优策略。
用通俗的话解释大数定理:在不知道模型参数的情况下,经过多次实验,将所得参数的平均近似为期望。大数定理是免模型的,而蒙特卡洛估计也是免模型的,二者不谋而合。
5.2 MC Basic算法
如何做到从有模型到免模型的转变,或者说如何在不知道两个概率分布的条件下得到 a c t i o n v a l u e action \ value action value 进而更新策略呢?
为了回答上述问题,我们需要借助 p o l i c y i t e r a t i o n policy \ iteration policy iteration。
即问题转变为:如何把 p o l i c y i t e r a t i o n policy \ iteration policy iteration 这种 m o d e l − b a s e d model-based model−based 算法转变为 m o d e l − f r e e model-free model−free 的算法呢?
算法中涉及两个概率分布的只有 q π k ( s , a ) q_{\pi_k}(s,a) qπk(s,a),所以问题转换为如何求这个 q π k ( s , a ) q_{\pi_k}(s,a) qπk(s,a)
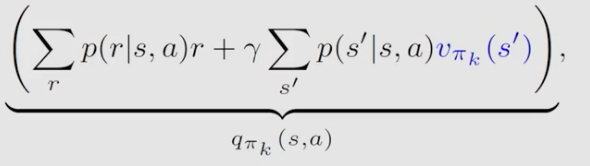
回到 q π k ( s , a ) q_{\pi_k}(s,a) qπk(s,a) 最初始的定义, q π k ( s , a ) = E [ G t ∣ S t = s , A t = a ] q_{\pi_k}(s,a)=\mathbb{E}[G_t|S_t=s,A_t=a] qπk(s,a)=E[Gt∣St=s,At=a],也是要求期望,何不用蒙特卡洛估计呢?
- 从 ( s , a ) (s,a) (s,a) 开始,采取策略 π k \pi_k πk,生成一个 e p i s o d e episode episode
- 一个 e p i s o d e episode episode 的 r e t u r n return return 称为 g ( s , a ) g(s,a) g(s,a)。( e p i s o d e episode episode 长度的选取会影响到策略的选择, e p i s o d e l e n g t h episode \ length episode length 越大,离目标越远的状态也能找到正确的策略。
- g ( s , a ) g(s,a) g(s,a) 即为 G t G_t Gt 的一个采样(sample)
- 对每一个 s s s 的每一个 a a a,生成一系列 e p i s o d e episode episode,对其每个 r e t u r n return return 相加求平均,近似为 q π k ( s , a ) q_{\pi_k}(s,a) qπk(s,a),即 q π k ( s , a ) = E [ G t ∣ S t = s , A t = a ] ≈ 1 N ∑ N i = 1 g ( s , a ) q_{\pi_k}(s,a)=\mathbb{E}[G_t|S_t=s,A_t=a]\approx \frac{1}{N}\underset{i=1}{\overset{N} \sum} g(s,a) qπk(s,a)=E[Gt∣St=s,At=a]≈N1i=1∑Ng(s,a)
- 更新策略
其实就是用蒙特卡洛估计来直接得到 q π k ( s , a ) q_{\pi_k}(s,a) qπk(s,a),然后进行 p o l i c y i m p r o v e m e n t policy \ improvement policy improvement。MC Basic算法需要采样的 e p i s o d e episode episode 过多,效率(efficiency)较低。
为什么不用 v a l u e i t e r a t i o n value \ iteration value iteration 进行转换呢?因为 v a l u e i t e r a t i o n value \ iteration value iteration 事先不知道策略,也就无法生成 r e t u r n return return 作为采样结果。
例子:
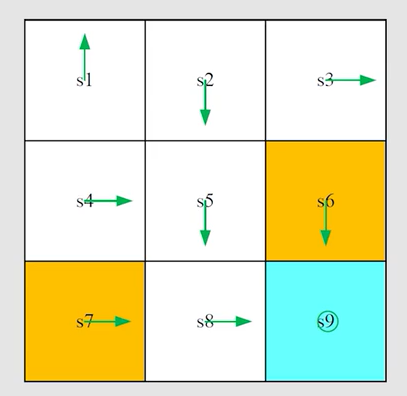
这个例子其实是有模型的,但并不妨碍介绍蒙特卡洛的思想。以 s 1 s_1 s1 为例,因为此时给定的策略概率都为1,所以采样一次即可(即使采样多次结果平均下来结果还是和采样一次一样)。先是求状态 s 1 s_1 s1 每个动作对应的 a c t i o n v a l u e action \ value action value


然后根据 a c t i o n v a l u e action \ value action value 更新策略:

5.3 MC Exploring Starts算法
核心思想,在每个 e p i s o d e episode episode 中充分利用数据:

现在要求得每一个 ( s , a ) (s,a) (s,a) 的 a c t i o n v a l u e action \ value action value 有两种方法,一种是从 ( s ′ , a ′ ) (s',a') (s′,a′) 开始经历一个 e p i s o d e episode episode,另一种是从别的 ( s , a ) (s,a) (s,a) 开始在其 e p i s o d e episode episode 中找到我需要的 ( s , a ) (s,a) (s,a)。但第二种方法是不确定会不会经过我需要的这样一个 ( s , a ) (s,a) (s,a) 的。
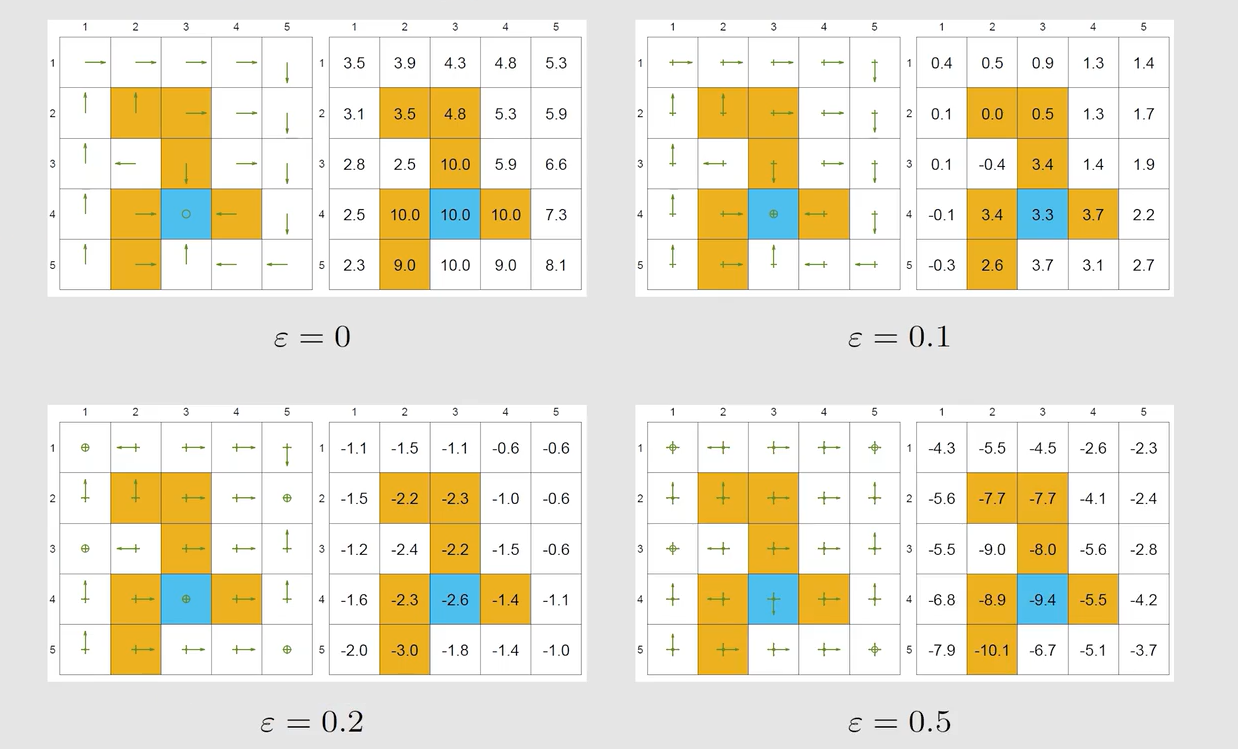
5.4 MC Epsilon-Greedy算法
如何确保MC Exploring Starts算法中提到的,可以从别的 ( s , a ) (s,a) (s,a) 开始在其 e p i s o d e episode episode 中找到我需要的 ( s , a ) (s,a) (s,a) 呢?
采用 ϵ − g r e e d y \epsilon-greedy ϵ−greedy 策略,保证在选择 a c t i o n action action 时是 s t o c h a s t i c stochastic stochastic 的,这样做能保证每个 ( s , a ) (s,a) (s,a) 都有概率能取到(即使概率较小,较大的概率还是取最大的 a c t i o n v a l u e action \ value action value 对应的 a c t i o n action action ),保证其有 e x p l o r a t i o n exploration exploration 。

如何将其与前面所讲的两个算法结合起来。其实就是在求出了 q π k ( s , a ) q_{\pi_k}(s,a) qπk(s,a) 后进行 p o l i c y i m p r o v e m e n t policy \ improvement policy improvement 时,采用 ϵ − g r e e d y \epsilon-greedy ϵ−greedy 策略:
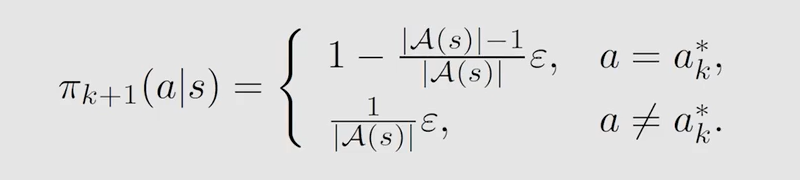
这样就可以做到从一个或几个 ( s , a ) (s,a) (s,a) 出发得到的 e p i s o d e episode episode 能覆盖到几乎所有的 ( s , a ) (s,a) (s,a)。
注意 ϵ \epsilon ϵ 的值不宜过大: