一、数论

1.1质数

定义:在所有大于1的自然数，如果只包含1和本身这两个约数，就被称为质数(素数).

质数的判断:试除法

bool is_prime(int n)
{if(n < 2) return false;for(int i = 2;i <= n / i;i ++){if(n % i == 0)return false;}return true;
}

分解质因数

基本思路:从小到大枚举n的所有约数。

void divide(int n)
{for(int i = 2;i <= n;i ++){if(n % i == 0){int s = 0;while(n % i == 0){n /= i;s ++;}printf("%d %d\n",i,s)}}
}

埃氏筛法

#include<iostream>
#include<algorithm>using namespace std;int primes[N],cnt;
bool st[N];void get_prime(int n)
{for(int i = 2;i <= n;i ++){if(!st[i]){primes[cnt ++] = n;for(int j = i + i;j <= n;j += i) st[j] = true;}}
}

线性筛法

保证了每个数都是被他的最小质因子所筛掉

#include<iostream>
#include<algorithm>using namespace std;int primes[N],cnt;
bool st[N];void get_primes(int n)
{for(int i = 2;i<= n;i ++){if(!st[i]) primes[cnt ++] = i;for(int j = 0;primes[j] <= n / i;j ++){st[primes[j] * i = true;if(i % primes[j] == 0) break;  //primes[j]一定是i的最小质因子}}
}

1.2约数

 试除法求约数

vector<int> get_divisors(int n)
{vector<int> res;for(int i = 1;i <= n / i;i ++)if(n % i == 0){res.push_back(i);if(i != n / i) res.push_back(n / i);}sort(res.begin(),res.end());return res;
}

约数个数与约数之和

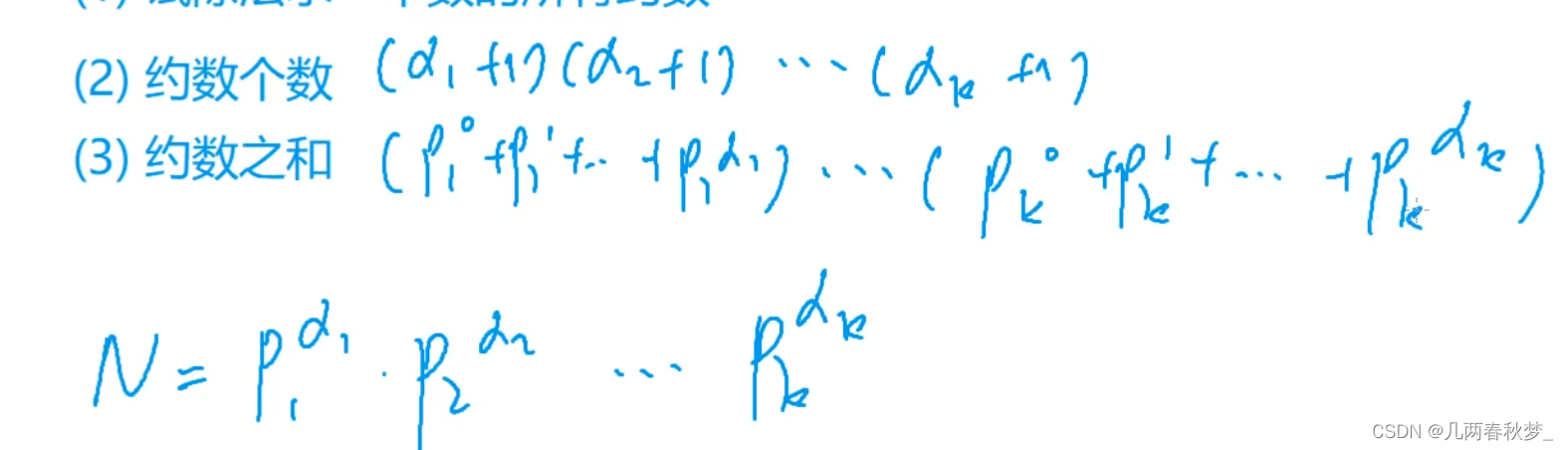
欧几里得算法

//返回a与b的最大公约数
int gcd(int a,int b)
{return b ? gcd(b,(a % b) : a);
}

二、欧拉定理

2.1欧拉函数

定义:X(n)表示1~n中与n互质的个数

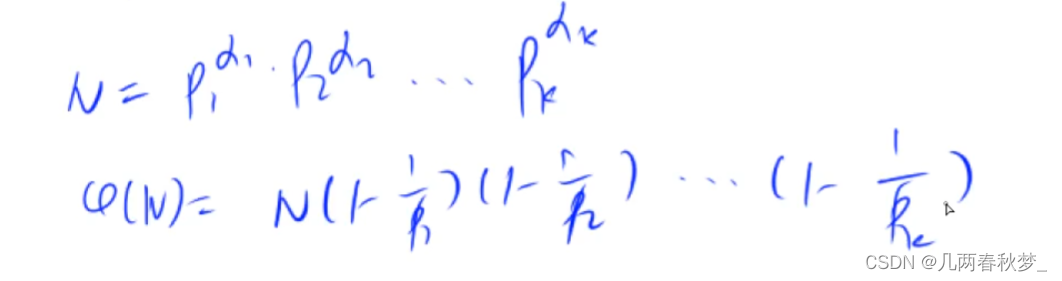
算法步骤:

1. 从1~N中去掉p1,p2,...,pk的倍数
2. 加上所有Pi * Pj的倍数
3. 减去所有Pi * Pj * Pk的倍数

#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;int main()
{int n;cin>>n;while(n --){int a;cin>>a;int res = a;//分解质因数for(int i = 2 ;i <= a;i ++){if(a % i == 0){res = res / i * (i - 1);while (a % i == 0) a /= i;}}if(a > 1) res = res / a * (a - 1);cout<<res<<endl;}return 0;
}

快速幂 

#include<iostream>
#include<algorithm>using namespace std;typedef long long LL;//求a^k % p
int main(int a,int k,int p)
{int res = 1;while(k){//如果当前k的末位为1，则if( k & 1) res = (LL)res * a % p;//删除k的末位k >>= 1;//把a平方a = (LL) a * a % p;}return res;
}
int main()
{int n;scanf("%d",&n);while(n --){int a,k,p;scanf("%d%d%d",&a,&k,&p);printf("%d\n",qmi(a,k,p));}return 0;
}