题目描述：

给定一个整数数组，它表示BST(即 二叉搜索树 )的 先序遍历 ，构造树并返回其根。

保证 对于给定的测试用例，总是有可能找到具有给定需求的二叉搜索树。

二叉搜索树 是一棵二叉树，其中每个节点， Node.left 的任何后代的值 严格小于 Node.val , Node.right 的任何后代的值 严格大于 Node.val。

二叉树的 前序遍历 首先显示节点的值，然后遍历Node.left，最后遍历Node.right。

示例 1：

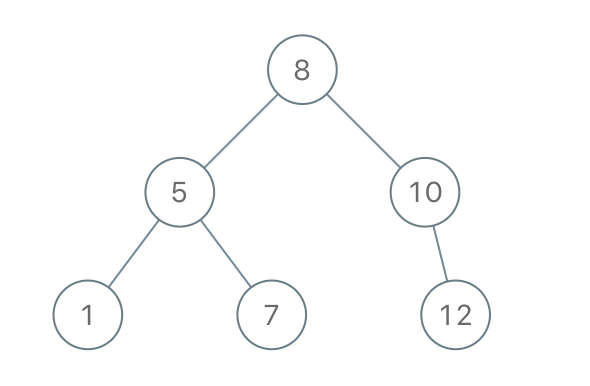
输入：preorder = [8,5,1,7,10,12]
输出：[8,5,10,1,7,null,12]

示例 2:
输入: preorder = [1,3]
输出: [1,null,3]

提示：
1 <= preorder.length <= 100
1 <= preorder[i] <= 10^8
preorder 中的值 互不相同

解题思路一：题目大致意思就是给定一个二叉树的前序遍历，求对应的二叉搜索树。一种比较特殊的点是「二叉搜索树」的中序遍历的结果是【有序序列】，故而我们可以对「前序遍历」的结果 【排序】 得到「中序遍历」的结果。从而依据这棵树的前序和中序遍历结果构建该「二叉搜索树」。

对应的题目是105. 从前序与中序遍历序列构造二叉树，感兴趣的可以看看。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:inorder = sorted(preorder)def myBST(preorder_left: int, preorder_right: int, inorder_left: int, inorder_right: int):if preorder_left > preorder_right:return None# 前序遍历中的第一个节点就是根节点preorder_root = preorder_left# 在中序遍历中定位根节点inorder_root = index[preorder[preorder_root]]# 先把根节点建立出来root = TreeNode(preorder[preorder_root])# 得到左子树中的节点数目size_left_subtree = inorder_root - inorder_left# 递归地构造左子树，并连接到根节点# 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素root.left = myBST(preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1)# 递归地构造右子树，并连接到根节点# 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素root.right = myBST(preorder_left + 1 + size_left_subtree, preorder_right, inorder_root + 1, inorder_right)return rootn = len(preorder)index = {element: i for i, element in enumerate(inorder)}return myBST(0, n-1, 0, n-1)

构造哈希表的目的是为了，O(1)时间找到中序遍历结果中的根节点。
时间复杂度：O(nlogn)排序的结果，构造二叉搜索树的时间复杂度为 O(n)
空间复杂度：O(n)

解题思路二：二分查找左右子树的分界线递归构建左右子树。可以找到的规律是前序遍历结果第一个是根节点，而后面的元素可以分为两个连续的数组，一个数组所有元素严格小于根节点，另一个数组所有元素严格大于根节点。困难在于快速找到这两个数组的分界线，这里用的是二分法。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:def dfs(preorder: List[int], left: int, right: int):if left > right: return Noneroot = TreeNode(preorder[left])if left == right: return rootl, r = left, rightwhile(l < r):mid = int(l + (r - l + 1) / 2)if preorder[mid] < preorder[left]: l = mid # 转到区间[mid, r]else : r = mid -1 # 转到区间[l, mid -1]# 其实最后l=r是最终的分界线root.left = dfs(preorder, left + 1, l)root.right = dfs(preorder, l + 1, right)return rootn = len(preorder)if n==0: return nullreturn dfs(preorder, 0, n-1)

时间复杂度：O(nlogn)，在找左右子树分界线的时候时间复杂度为O(logn)；
空间复杂度：O(n)

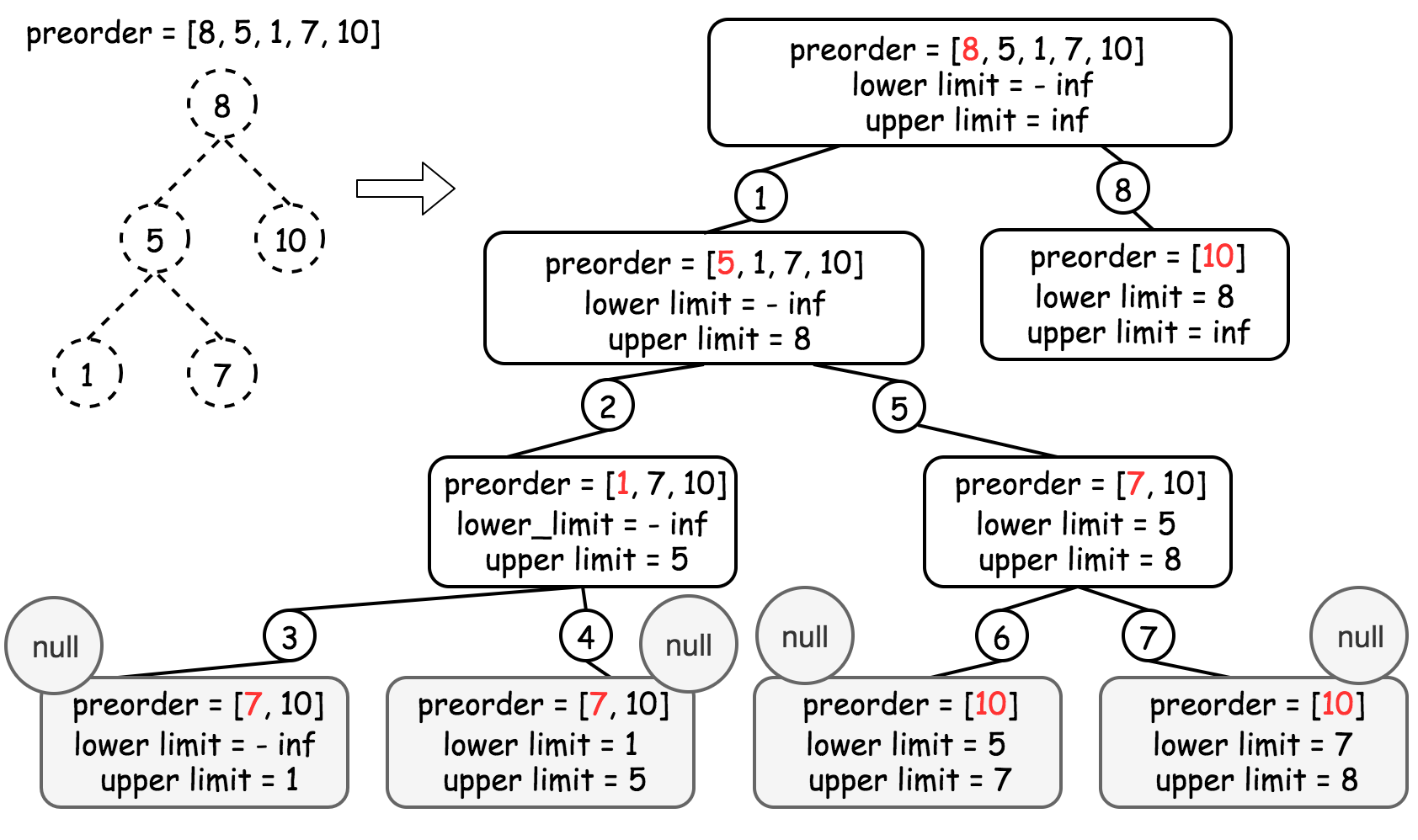
解题思路三：根据数值上下界递归构建左右子树，我们使用递归的方法，在扫描先序遍历的同时构造出二叉树。我们在递归时维护一个 (lower, upper) 二元组，表示当前位置可以插入的节点的值的上下界。如果此时先序遍历位置的值处于上下界中，就将这个值作为新的节点插入到当前位置，并递归地处理当前位置的左右孩子的两个位置。否则回溯到当前位置的父节点。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:n = len(preorder)index = 0def dfs(lowerBound: int, upperBound: int):nonlocal index  # 将index声明为非局部变量if index == n: return Nonecur = preorder[index]if cur < lowerBound or cur > upperBound: return Noneindex += 1root = TreeNode(cur)root.left = dfs(lowerBound, cur)root.right = dfs(cur, upperBound)return rootif n==0: return nullreturn dfs(float('-inf'), float('inf'))

时间复杂度：O(n)
空间复杂度：O(n)

解题思路四：单调栈，思路是维护一个栈顶小栈顶大的单调栈，遍历一遍前序遍历结果。如果当前元素大于栈顶元素，则循环出栈找到其父节点node。如果父节点的元素值小于子节点的元素值，则子节点为右孩子，否则为左孩子。代码逻辑其实很简单。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:n = len(preorder)if n==0: return nullroot = TreeNode(preorder[0])stack= [root]for i in range(1,n,1):node = stack[-1]currentNode = TreeNode(preorder[i])while stack and stack[-1].val < currentNode.val: node = stack.pop()if node.val < currentNode.val: node.right = currentNodeelse : node.left = currentNodestack.append(currentNode)return root

时间复杂度：O(n)仅扫描前序遍历一次。
空间复杂度：O(n)用来存储栈和二叉树。