官方学习资料
主要是的学习资料是, 官方文档 和官方博客。相关文章还是挺多 挺不错的 他们更新也比较及时。有最新的东西 都会更新出来。
es scdn官方博客
这里简单列一些,还有一些其他的,大家自己感兴趣去看。
什么是向量数据库
Elasticsearch:向量数据库的真相-CSDN博客
什么是向量嵌入
什么是大语言模型(LLM)
什么是语义搜索
向量搜索的优势
什么是机器学习
关于多模态
这个是多模态检索。目前es只能做文本类转向量的模型导入。不支持图片转向量的模型导入。(clip是双塔模型,一个负责文本转向量,一个负责图片转向量。我测过了,图片转向量模型不支持导入)如果用es做多模态。还是要在外边部署模型。 整体体验不好。而且模型导入es,是收费的白金版。 最佳实践(不付费玩法)应该是完全在外边做转向量。 考虑付费,可以用es
学术界前沿的研究对比
这个是学术稍微前沿一点的研究。里边包含的论文,感兴趣可以看看。里边探讨对比了关于BM25和向量检索的效果。还包含稀疏向量相关的知识。
关于稀疏向量
稠密向量有一个致命问题。 检索速度,以及做嵌入的速度。太慢,现在最先进的方向是稀疏向量
这里边有对比 语义检索 和 BM25的效果对比。(最佳实践是两者结合,做内容召回。两者可以互补)根据官方提供的稀疏向量的模型测试结果如下图所示,据说20个场景有19个都优遇BM25.
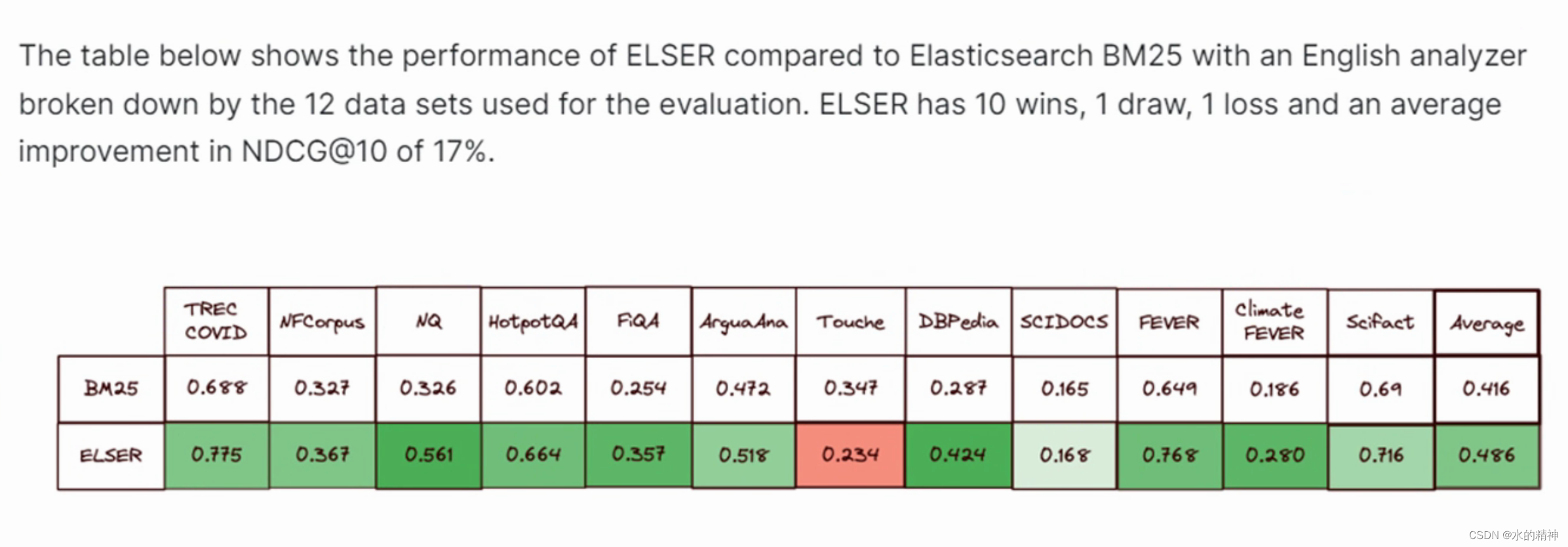
这是稀疏向量模型的转换效果,应该不会多花费空间。它的维度相对低。
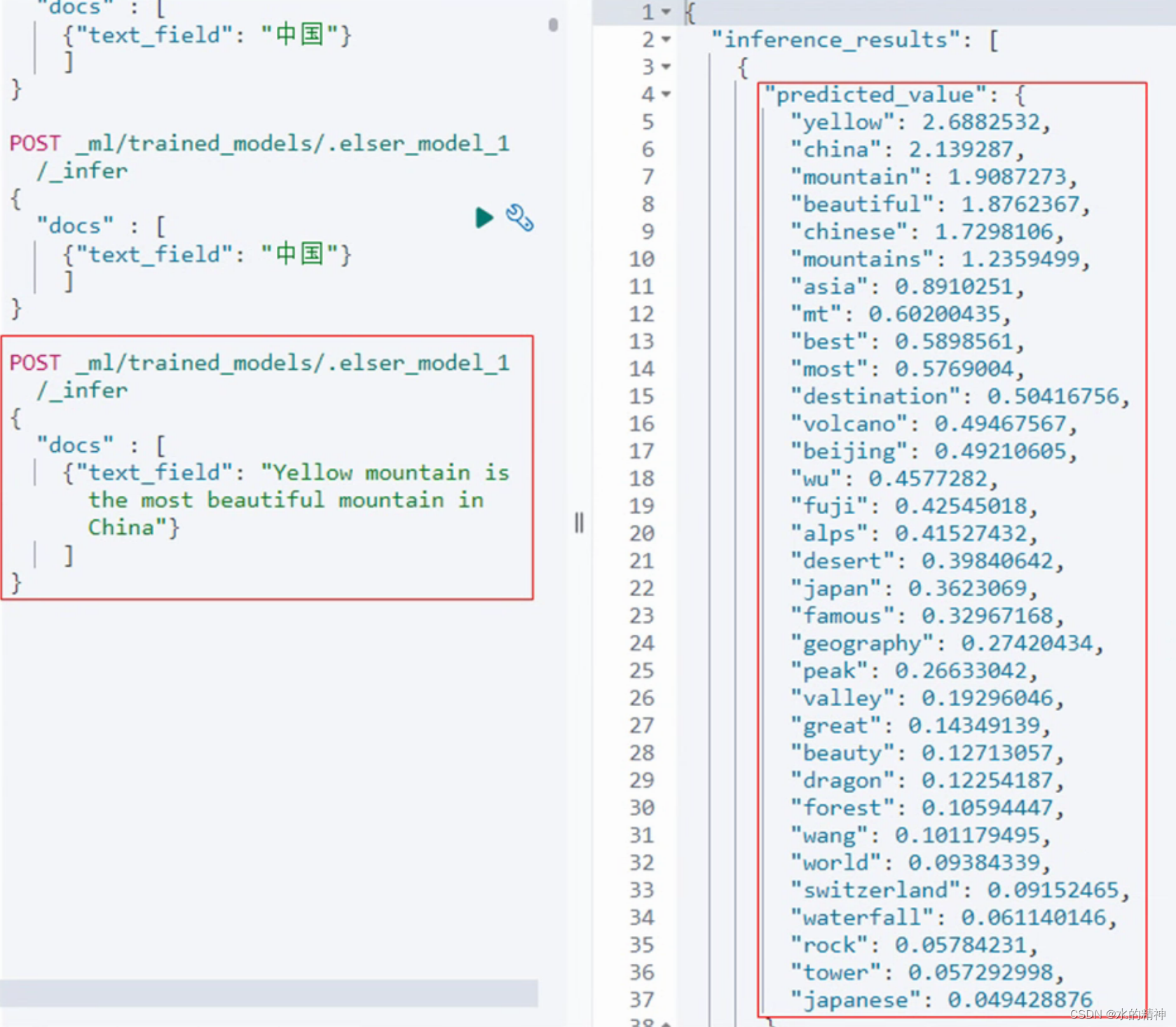
这里有我的一篇文章,国内生产实践经验帖。ES-ELSER 如何在内网中离线导入ES官方的稀疏向量模型(国内网络环境下操作方法)-CSDN博客
如何做向量嵌入
模型转向量,简单来讲,是利用机器学习模型把一块文本(数据),映射到网络空间内,同样问题(query)也是用同一个模型,映射到网络空间内。然后计算cosin值,也就是夹角越小,就越相近。
我在生产实践中,是选择使用es来的机器学习模块倒入hugging face上的NLP模型,来做文本嵌入。
这里有一篇我自己写的国内环境下。如何在es中导入NLP模型。elasticsearch 内网下如何以离线的方式上传任意的huggingFace上的NLP模型(国内避坑指南)-CSDN博客
这里还有一个例子,是在es中使用 E5 嵌入模型进行多语言向量搜索
向量检索简单举个例子
data 是一篇文章的内容。这个内容最终可能是切分成N个片段。 然后通过模型把每个片段都转成向量,然后再把向量存到向量库。
例如,第一个段落 片段转完是 [1.0000009,0.11111111,0.899998]
然后问题,也转成向量可能是 [1.0044449,0.55551111,0.449998]
然后通过计算这两个数组,的cosin值,然后再比较 其它片段和问题的cosin值(当然还可以用其它计算方式),然后做个排序,然后把topN小的返回。这就是KNN最邻近搜索。
关于相关性或者说相似性
相似不相似,其实更多是依赖模型效果好不好。向量库都只是起计算作用。关于向量库的选择,只需要看该向量数据库的稳定性,数据承载能力(也就是能存多少数据,是否满足业务需求。)已经向量数据库实现的向量检索算法都有哪些(实际上目前学术界也就那么多)。还有就是该库的检索性能如何,稳定性如何,能够满足业务需求。但是不要想着在向量数据库上去提升搜索相关性的事情,因为相关性和库没有太大关系。如何要研究提升召回效果。应该去考虑选择什么样的机器学习模型效果更好,还要考虑模型的语言能力,是否支持多语种。例如你在英文模型下做中文数据的embedding,效果肯定会很差。此外不同的业务应该选择自己的模型,加上微调。而不是一个大一统的模型。另外一个提升相关性的方向是探索数据切割的规则,针对不同类型的数据做不同的切分。
实际上利用向量检索的相关性效果,还确实是比BM25好的。但是它不是绝对的,在关键词精准匹配场景下,BM25算法更好一些。
如何选择模型
语义检索系统如何选择合适的embedding模型-CSDN博客
使用模型做文本陷入,如何做数据切分,不丢失语义
目前这一块探索还比较少。根据看过的一些案例,基本上推荐在500个token,300-400个字。再多了就会丢失语义。这里还需要摸索和测试一下。
ES支持混合检索吗? 向量检索+倒排索引
es ANN搜索
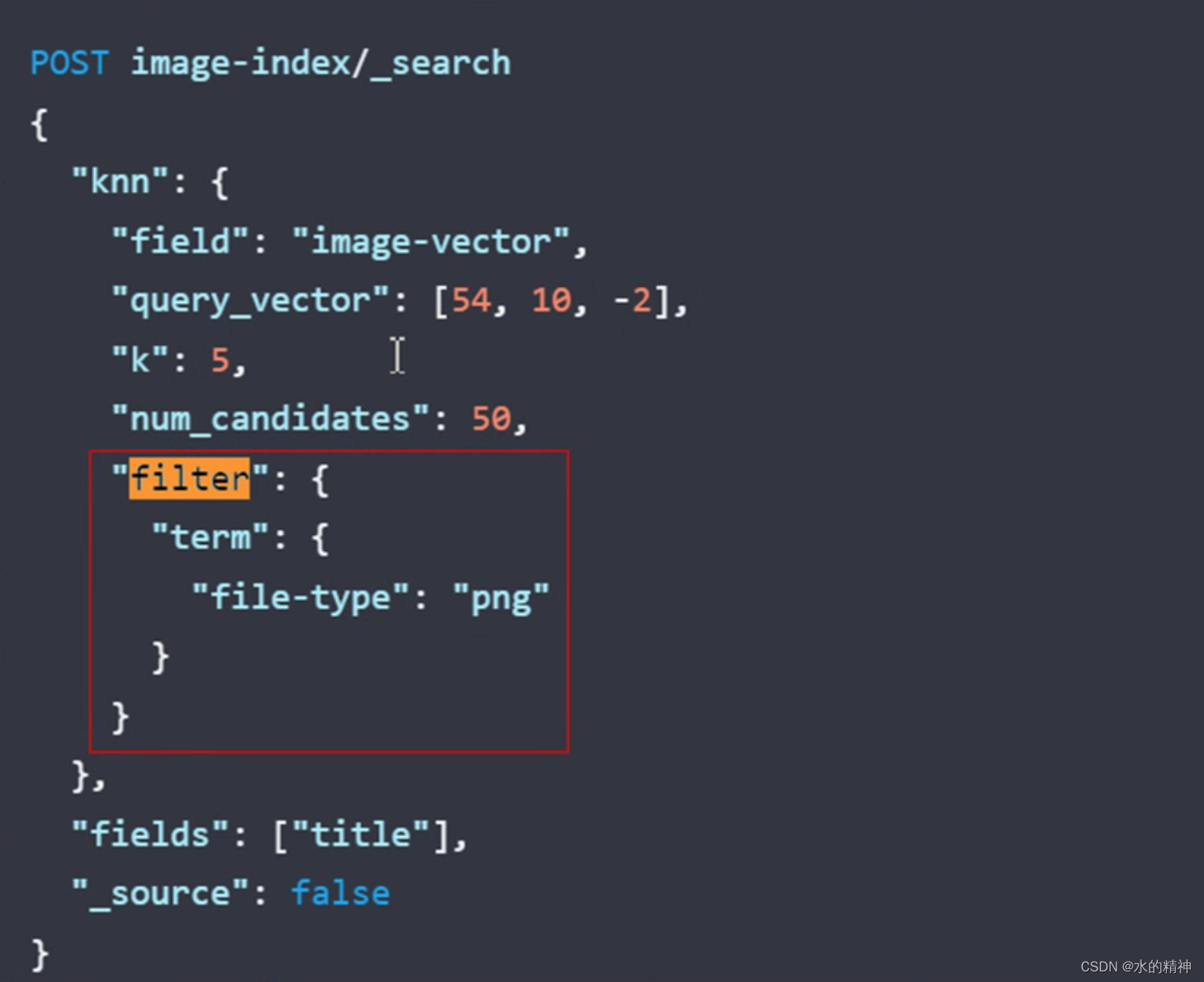
这样可以先筛选数据。然后剩下的在做 knn搜索。这个逻辑会先走倒排搜索。
提供一个向量检索的案例
腾讯es云,最近写的最佳实践
关于请求改写经验
美团的查询改写



Java 基础语法)
User-Managed Incomplete Recovery)
)

开发板的Android10的SDK)

)

(查看开头、从开头查看、从起始查看、反向导航、反向查找))







