🌈个人主页: Aileen_0v0
🔥系列专栏: 数据结构与算法
💫个人格言:"没有罗马,那就自己创造罗马~"
这篇博客主要探索的是计算机科学常见问题---搜索算法
“时间紧，任务重！”
话不多说，开始今天的学习之旅吧⛵~
目录
搜索
定义
关键字-in
顺序搜索
无序表的顺序搜索过程
无序表的顺序搜索代码实现
分析顺序搜索算法
有序列表
有序列表的顺序搜索过程编辑
无序表的顺序搜索代码实现
搜索
定义
搜索是指从元素集合中找到特定元素的算法过程。
搜索过程通常返回True 或 False 来表示元素是否在集合中。
有时也可以修改搜索过程，使它返回目标元素的位置。
为了更好的打好算法基础，我们这次先探索搜索的元素是否存在这一问题。
关键字-in
in是Python中的关键字，用于判断一个元素是否存在于一个容器中。可以用于列表、元组、字典、集合等数据类型。它可以被用于for循环语句 和 if语句中。
我们之前做Python每日一练时我曾科普过Python中 我们可以通过运算符 —— in 去检查元素是否在列表中。
print(15 in [1,2,3])
print(15 in [1,2,3,15])运行结果：
顺序搜索
线性结构（数组、链表、栈、队列等）都有下标。每个数据项都有一个相对于其它数据项的位置。
Python的列表 ，数据项的位置就是其下标。
因为下标是有序的，So 我们能够进行 顺序访问 及 顺序搜索。
无序表的顺序搜索过程
下图展示了顺序搜索的过程。
无序表的顺序搜索代码实现
def sequential_search(a_list,item):pos = 0while pos < len(a_list):if a_list[pos] == item:return Truepos += 1return Falseprint(sequential_search([1,2,4,5,9],5))从列表第一个元素开始， 沿着下表顺序逐个查看，直到找到目标元素或者到达列表末尾。
若查完列表后仍未找到目标元素，则说明目标元素不在列表中。
分析顺序搜索算法
分析搜索算法前，首先需要先定义 计算的基本单元---解决问题过程中不断重复的的某一步。
对搜索来说，记录 比较的次数 是合理的 性能指标。
每次比较只有两个结果： 找到目标元素，或未找到。
假设元素排列无序，则目标元素在每一个位置出现的可能都相同。
要确定目标元素是否在列表中，唯一的方法就是将它与列表中的每个元素都比较一次。
若列表中有n个元素，那么顺序搜索要经过 n 次比较后才能确定目标元素不在列表中。如果列表含目标元素，分析起来更复杂。实际上有 3 种可能的情况：
最好情况是目标元素位于列表的第一个位置，则只需比较一次;
最坏情况是目标元素位于最后一个位置，则需要比较 n次。
平均情况是目标元素位于中间位置，则需要比较 n / 2次。 --> 当n增大，系数则可省略，所以顺序搜索时间复杂度为O（n）。
有序列表
有序列表的顺序搜索过程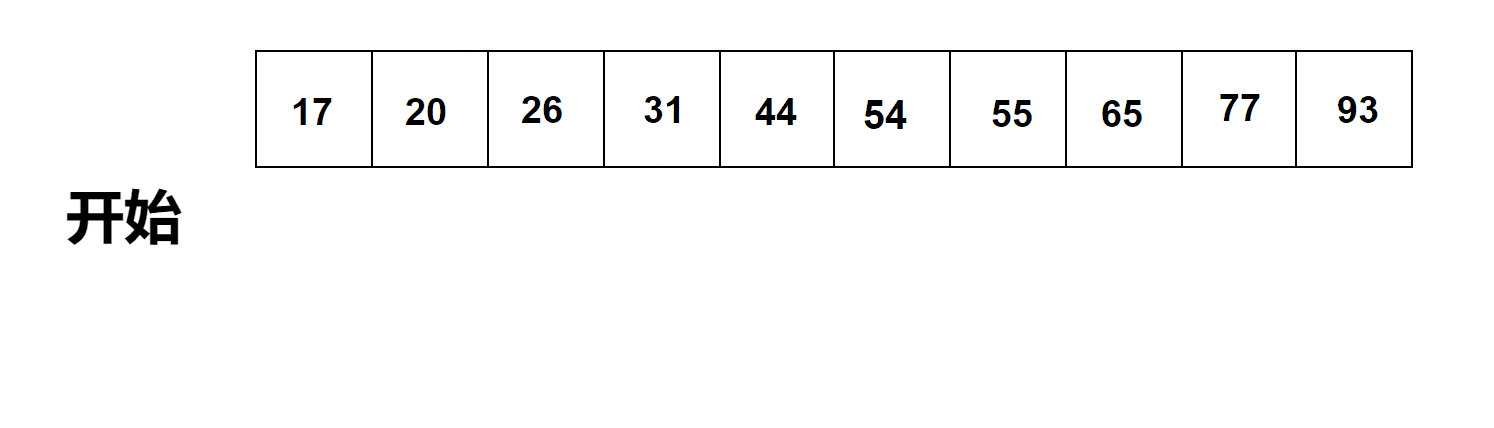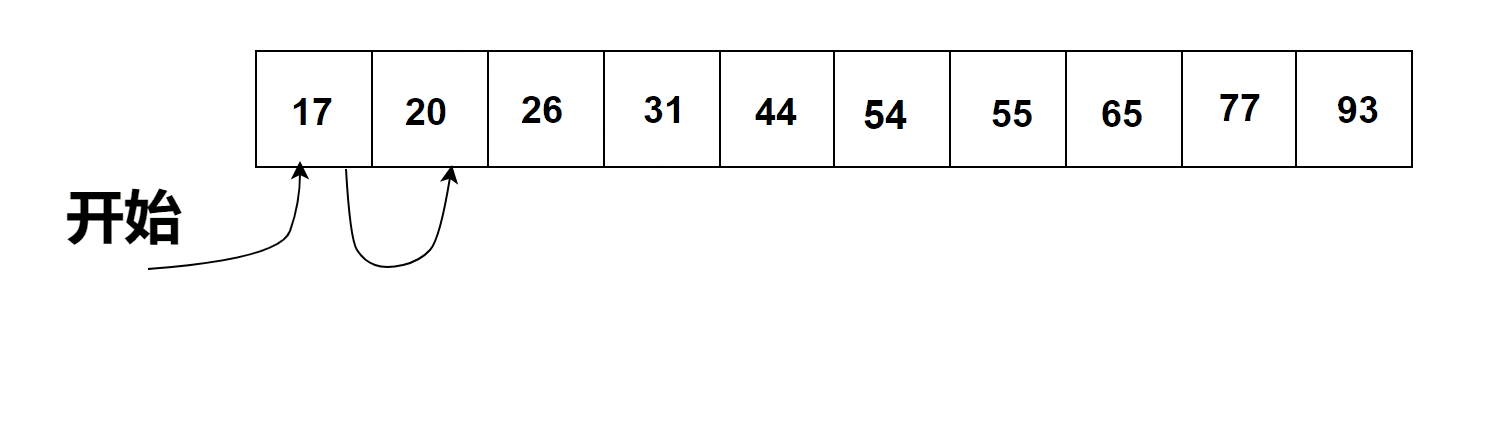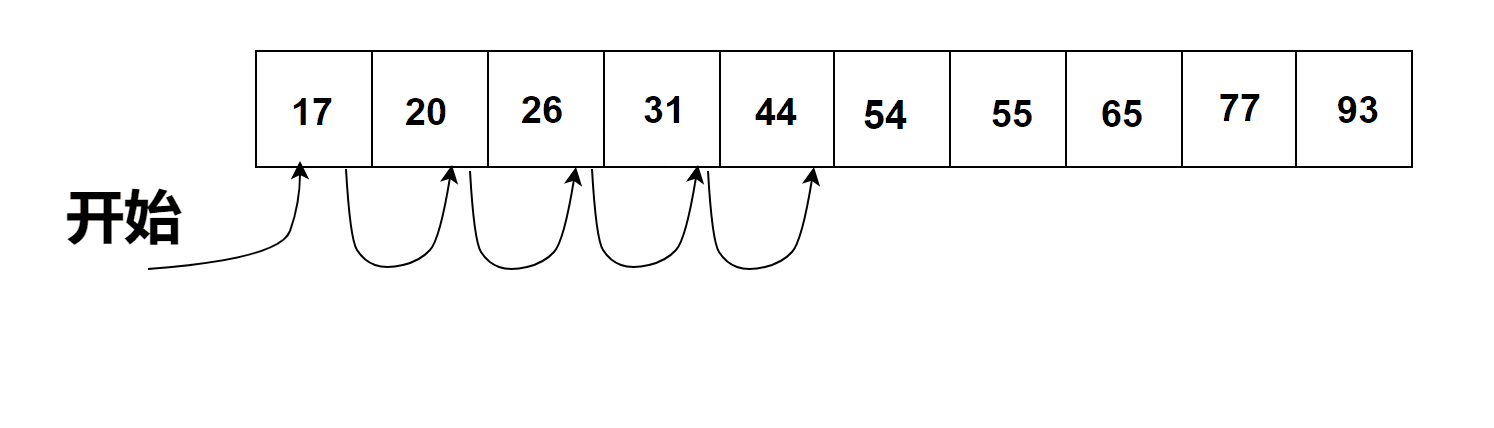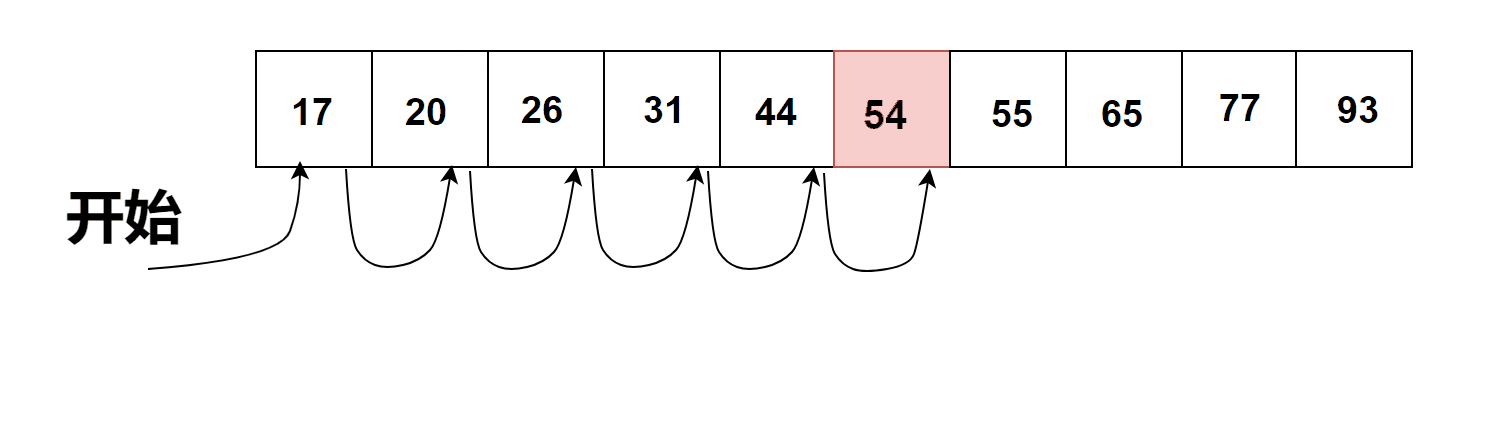
通过观察上图有序列表列表中的顺序搜索过程我们可以得出以下结论：
当元素按升序排列。
如果存在目标元素，那么它出现在 n个位置中任意一个位置的可能性仍然一样大，因此比较次数与在无序列表中相同。
But，如果不存在目标元素，那么搜索效率就会提高。---> 因为当找到比目标元素大的数的时候程序就会停止搜索。
无序表的顺序搜索代码实现
#有序表的顺序搜索
def ordered_sequential_search(a_list,item):pos = 0while pos < len(a_list):if a_list[pos] == item:return Trueelif a_list[pos] > item:return Falsepos += 1return False
print(ordered_sequential_search([1,2,4,5,9],6))下表总结了，在有序表中搜索时的比较次数。
最好情况：只需比较1次。 平均情况：比较 n / 2 次，但时间复杂度仍是O（n）。
总结：只有当列表不存在目标元素时，有序排列的元素，才能提高顺序搜索的效率。
📝总结：
本篇文章介绍了搜索算法以及，有序列表在搜索算法中 的优势，前提条件是：只有当元素不在列表中时，有序排列的元素，才能提高顺序搜索的效率。
