并查集(Union-find Sets)是一种非常精巧而实用的数据结构,它主要用于处理一些不相交集合的合并问题.一些常见的用途有求连通子图,求最小生成树Kruskal算法和最近公共祖先(LCA)等.
并查集的基本操作主要有:
.1.初始化
2.查询find
3.合并union
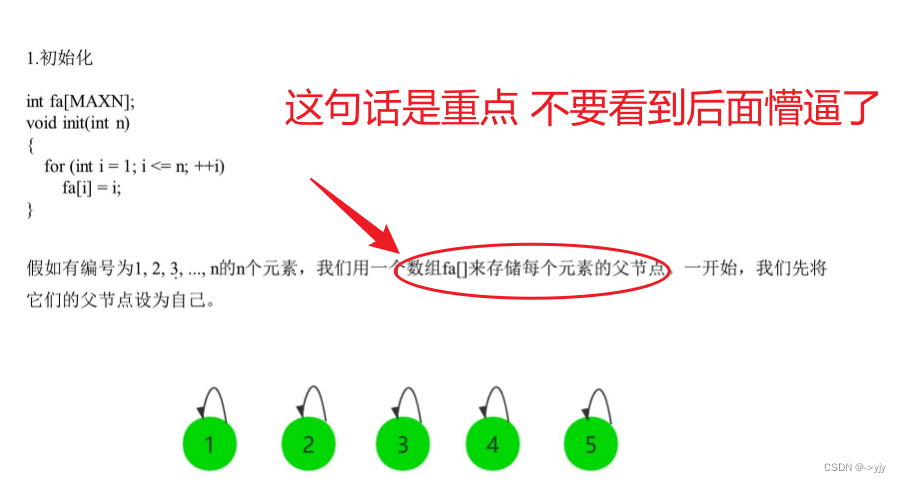

一般我们都会采用路径压缩 这样效率更加高



#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
#define MAXN 20001
int fa[MAXN];
void init(int n) {for (int i = 1; i <= n; i++) {fa[i] = i;}//初始化
}
int find(int x) {if (x == fa[x]) {return x;}else {fa[x] = find(fa[x]);//路径压缩 也就是一直找到祖先return fa[x];}
}
void unionn(int i, int j) {int i_fa = find(i);//找到i的祖先int j_fa = find(j);//找到j的祖先fa[i_fa] = j_fa;//i的祖先指向j的祖先 反过来也可以
}
int main() {int n, m, x, y, q;scanf("%d", &n);init(n);scanf("%d", &m);for (int i = 1; i <= m; i++) {scanf("%d%d", &x, &y);unionn(x, y);}scanf("%d", &q);for (int i = 1; i <= q; i++) {scanf("%d%d", &x, &y);if (find(x) == find(y)) {printf("Yes\n");}else {printf("No\n");}}return 0;
}
或者这样写
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;const int N = 20010;int n, m;
int p[N];
int find(int x) {if (p[x] != x)p[x] = find(p[x]);return p[x];
}
int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++) p[i] = i;while (m--) {int a, b;scanf("%d%d", &a, &b);p[find(a)] = find(b);//合并 a->b}scanf("%d,&m");while (m--) {int a, b;scanf("%d%d", &a, &b);if (find(a) == find(b))puts("yes");else puts("no");}return 0;}

#include<iostream>
using namespace std;const int N = 10010;int n, m;
int p[N];int find(int x) {if (p[x] != x)p[x] = find(p[x]);return p[x];
}
int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++) p[i] = i;char op[2];//读入操作的字符串 因为字符串后面有'\0'所以要存多一位while (m--) {int a, b;scanf("%s%d%d",&op ,&a, &b);if(*op=='M')p[find(a)] = find(b);//合并else {if (find(a) == find(b)) {puts("Yes");}else {puts("No");}}}return 0;
}
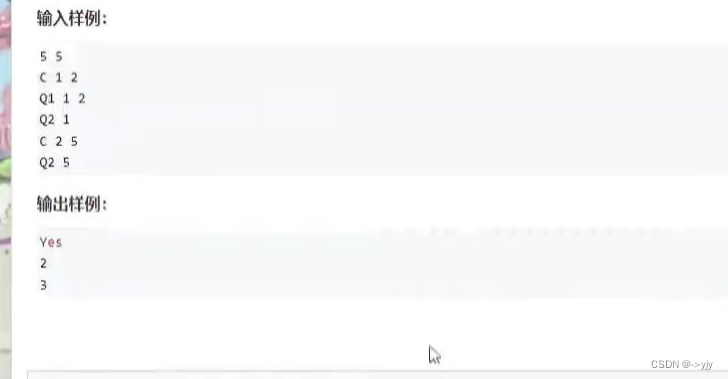
#include<iostream>
using namespace std;
const int N = 10010;int n, m;
int p[N], s[N];int find(int x) {if (p[x] != x)p[x] = find(p[x]);return p[x];
}
int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++) p[i] = i, s[i] = 1;while (m--){char op[3];int a, b;scanf("%s", &op);if (*op == 'C') {scanf("%d%d", &a, &b);a = find(a), b = find(b);if (a != b) {//如果相等证明他们在同一个祖先中s[b] += s[a];p[a] = b;}else if (*op == 'Q1') {scanf("%d%d", &a, &b);if (find(a) == find(b)) {puts("Yes\n");}else {puts("No\n");}}else {scanf("%d", &a);printf("%d\n", s[find(a)]);}}}return 0;
}












覆盖优化 - 附代码)
)


概念)
)
和迁移学习(Transfer Learning)的详细解释以及区别(系列1))
