🔥博客主页: 【小扳_-CSDN博客】
❤感谢大家点赞👍收藏⭐评论✍


文章目录
1.0 从前序与中序遍历序列来构造二叉树
1.1 实现从前序与中序遍历序列来构造二叉树思路
1.2 代码实现从前序与中序遍历序列来构造二叉树
2.0 从中序与后序遍历序列构造二叉树
2.1 实现从中序与后序遍历序列后遭二叉树思路
2.2 代码实现从中序与后序遍历序列来构造二叉树
3.0 根据后缀表达式创建二叉树
3.1 实现后缀表达式创建二叉树思路
3.2 代码实现后缀表达式创建二叉树
4.0 相同的树
4.1 实现判断两颗树是否相同思路
4.2 代码实现相同树
5.0 另一颗树的子树
5.1 实现判断是否为另一颗树的子树
5.2 代码实现判断是否为另一颗树的子树
1.0 从前序与中序遍历序列来构造二叉树
题目:
给定两个整数数组
preorder和inorder,其中preorder是二叉树的先序遍历,inorder是同一棵树的中序遍历,请构造二叉树并返回其根节点。示例 1:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7]OJ链接:
105. 从前序与中序遍历序列构造二叉树
1.1 实现从前序与中序遍历序列来构造二叉树思路
具体思路为:前序遍历的流程先是访问根节点,到左子树,再到右子树的顺序;中序遍历的流程先是左子树,到访问根节点,再到右子树。因此,在前序的序列中的第一个元素就是该树的根节点的值,然后再通过中序的序列中遍历找根节点。接着就可以将其中序的序列进行拆分,在中序序列中根节点的值的左边部分的序列为左子树,在中序序列中根节点的值的右边部分序列为右子树。又接着将前序序列进行拆分,从索引为 1 开始,长度为:与中序序列中左子树的序列数量是一致的,将这一部分称为左子树;从索引 (1+长度)开始到该序列的结束,将这一部分称为右子树。接下来就是子问题了,通过递归,找到当前节点的左右子树。
具体例子:前序序列 pre = {3,9,20,15,7},中序序列 in = {9,3,15,20,7} 。先找到该树的节点值 int rootValue = pre[0], TreeNode root = new TreeNode(rootValue),创建该树的根节点。接着对中序序列遍历来找到根节点的值,i == 1 ,在中序序列中找左右子树:在索引在该区间 [0,1)是节点的左子树,而在索引为 [2,5)区间是节点的右子树。在前序序列中找左右子树:在索引为 [1,2)是该节点的左子树,而在索引为 [2,5)区间是节点的右子树。
子问题:那么现在得到了左子树的前序序列 pre = { 9 } ,左子树的中序序列 in = { 9 },接下来的流程跟以上的流程是一样的,先找到该子树的根节点值 9 ,然后创建一个值为 9 的根节点。接着,遍历中序序列来找到根节点的值,该根节点的左部分就是左子树,该节点的右部分就是右子树。那么这里的左右子树都为空,因此节点为 9 的根节点没有左右子树了。
往上回溯:来到根节点值为 3 的节点。现在得到了右子树的前序序列 pre = {20,15,7} ,右子树的中序序列 in = {15,20,7} ,接下来的过程是一摸一样的,先找到该子树的根节点值为 20 ,创建值为 20 的根节点。然后在中序序列中进行遍历找到根节点的左右子树 :左子树序列为 {15},右子树序列为 {7},接着在前序序列中找左右子树:左子树序列为 {15},右子树序列为 {7} 。又得到了左右前中序列,按同样的道理继续下去即可,通过上面的结论,当左子树前序 {15} 与左子树中序 {15} 一样时,那么在当前的节点值为 15 的根节点没有左右子树了。同理,当右子树前序 {7} 与右子树中序 {7} 一样时,那么在当前的节点值为 7 的根节点没有左右子树了。
最后回溯,根节点值为 20 的左子树的根节点为 15,右子树的根节点为 7 ,链接起来,一直回溯到结束返回的最后的节点就是该树的根节点(值为 1 的根节点)。
需要注意的是:注意左闭右开。因为是同一颗树,在前序中的左右子树的长度跟中序中的左右子树的长度是一样的。
1.2 代码实现从前序与中序遍历序列来构造二叉树
//根据前序与中序来构造二叉树public TreeNode prevAndInOrderConstructTree(int[] prevOrder, int[] inOrder) {if (prevOrder.length == 0) {return null;}int rootValue = prevOrder[0];TreeNode root = new TreeNode(rootValue);for (int i = 0; i < inOrder.length; i++) {if (inOrder[i] == rootValue) {int[] inLeft = Arrays.copyOfRange(inOrder,0,i);int[] inRight = Arrays.copyOfRange(inOrder,i+1,inOrder.length);int[] prevLeft = Arrays.copyOfRange(prevOrder,1,i + 1);int[] prevRight = Arrays.copyOfRange(prevOrder,i+1,inOrder.length);root.left = prevAndInOrderConstructTree(prevLeft,inLeft);root.right = prevAndInOrderConstructTree(prevRight,inRight);}}return root;}只要某一个序列无论是前序或者是中序序列的长度为 0 ,都代表创建二叉树过程结束了。
2.0 从中序与后序遍历序列构造二叉树
题目:
给定两个整数数组
inorder和postorder,其中inorder是二叉树的中序遍历,postorder是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。示例 1:
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] 输出:[3,9,20,null,null,15,7]OJ链接:
106. 从中序与后序遍历序列构造二叉树
2.1 实现从中序与后序遍历序列后遭二叉树思路
具体思路为:中序的序列先访问左子树,再访问根节点,最后到右子树。后序的序列先访问左子树,再访问右子树,最后才到根节点。因此,可以从后序序列中的最后一个元素得到根节点的值,然后利用该值来创建根节点。接着,在中序序列中遍历查找根节点的值,在中序序列中根节点值左边的序列为左子树序列,在中序序列中根节点的右边为右子树的序列。再接着再后序中获取左子树的序列:从索引为 0 开始长度是中序序列得到的左子树的长度;从后序序列中获取右子树序列:除了左子树的序列和根节点值元素,其余就是右子树的序列了。接下来就是子问题了,递归下去,返回当前的根节点。
具体例子:中序序列 in = {9,3,15,20,7},后序序列 post = {9,15,7,20,3},通过后序得到该树的根节点的值 3,由这个值来创建值为 3 的根节点。接着通过遍历中序序列,找到值为 3 来定位左右子树,左子树的序列为:{9} ,右子树的序列为:{15,20,7} 。再从中序序列中定位左右子树,左子树为:{9},右子树为:{15,7,20} 。现在得到了左右中后序列,中序左子树:{9} ,后序左子树:{9},通过后序得到根节点,再从中序定位该子树的根节点,这里根节点值为 9 的根节点的左右子树均为 null 。接着回溯,返回的该子树的根节点。
再到右子树中序 {15,20,7} ,右子树后序 {15,7,20},通过后序序列的最后一个值来创建该子树的根节点,在中序中遍历找到该根节点的值,定位该节点的左右子树。中序的左子树序列 {15},右子树序列 {7};后序的左子树序列 {15},后序的右子树序列 {7} 。
再接着递归,得到左子树中序 {15} ,左子树后序 {15}。通过后序的最后一个元素就是根节点的值来创建该子树的根节点,然后在中序中定位该根节点的左右子树,这里的左右子树都为 null ,返回根节点即可。得到右子树中序 {7},右子树后序 {7},通过后序的最后一个元素为根节点的值来创建该子树的根节点,然后在中序中定位该根节点的左右子树,恰好,这里的左右子树都为 null ,返回根节点即可。
最后回溯过程,根节点值为 1 的节点的左子树的根节点为 9 的节点,右子树的根节点为 20 的节点。
2.2 代码实现从中序与后序遍历序列来构造二叉树
//根据中序与后序来构造二叉树public TreeNode inAndPostConstructTree(int[] inOrder, int[] postOrder) {if (inOrder.length == 0) {return null;}int rootValue = postOrder[postOrder.length-1];TreeNode root = new TreeNode(rootValue);for (int j = 0; j < inOrder.length; j++) {if (rootValue == inOrder[j]) {int[] inLeft = Arrays.copyOfRange(inOrder,0,j);int[] inRight = Arrays.copyOfRange(inOrder,j+1,inOrder.length);int[] postLeft = Arrays.copyOfRange(postOrder,0,j);int[] postRight = Arrays.copyOfRange(postOrder,j,postOrder.length-1);root.left = inAndPostConstructTree(inLeft,postLeft);root.right = inAndPostConstructTree(inRight,postRight);}}return root;}需要注意的定位左右子树的序列长度,中序与后序的左右子树都是一一对应的。也因此,当无论任意一个序列结束,都代表着构造二叉树过程结束。
3.0 根据后缀表达式创建二叉树
后缀表达式也叫逆波兰表达式,是一种不需要括号的表达式表示方法。在后缀表达式中,运算符总是在操作数的后面,因此可以通过从左到右扫描表达式来创建二叉树。
3.1 实现后缀表达式创建二叉树思路
具体思路为:若遇到数字将其压入栈中;若遇到操作符时,将栈中的右左元素弹出栈,操作符节点进行链接弹出来的左右子树,需要注意的是,第一个弹出来的是右操作数,第二个才是左操作数。链接完之后,将其压入栈中即可。循环结束条件为:将后缀表达式遍历完就结束。最后返回栈中的栈顶元素,就是该树的根节点。
3.2 代码实现后缀表达式创建二叉树
//根据后缀表达式创建二叉树public TreeNode suffixCreateTree(String[] s) {LinkedList<TreeNode> stack = new LinkedList<>();for (int i = 0; i < s.length; i++) {String ch = s[i];switch (ch) {case "+","-","*","/" -> {TreeNode right = stack.pop();TreeNode left = stack.pop();TreeNode t = new TreeNode(ch);t.right = right;t.left = left;stack.push(t);}default -> {stack.push(new TreeNode(ch));}}}return stack.peek();}
4.0 相同的树
题目:
给你两棵二叉树的根节点
p和q,编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
输入:p = [1,2,3], q = [1,2,3] 输出:trueOJ链接:
100. 相同的树
4.1 实现判断两颗树是否相同思路
具体思路为:使用递归实现,第一种情况:若一个子树为 null ,另一个子树不为 null ,返回 false ;第二种情况:若两个子树都为 null ,则返回 true 。第三种情况:若两个子树的根节点的值不相同时,返回 false 。子过程,判断完左子树,还需判断右子树。
4.2 代码实现相同树
class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {if( p != null && q == null || p ==null && q != null) {return false;}if(p == null && q == null ){return true;}if(p.val != q.val) {return false;}return isSameTree(p.left, q.left) && isSameTree(p.right,q.right);} }
5.0 另一颗树的子树
题目:
给你两棵二叉树
root和subRoot。检验root中是否包含和subRoot具有相同结构和节点值的子树。如果存在,返回true;否则,返回false。二叉树
tree的一棵子树包括tree的某个节点和这个节点的所有后代节点。tree也可以看做它自身的一棵子树。示例 1:
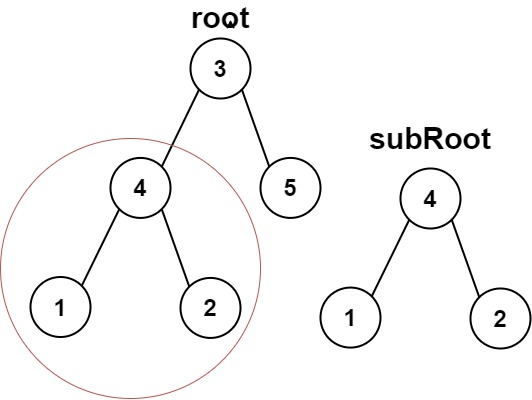
输入:root = [3,4,5,1,2], subRoot = [4,1,2] 输出:trueOJ链接:
572. 另一棵树的子树
5.1 实现判断是否为另一颗树的子树
具体思路为:最根本的问题就是判断是否为相同的树,判断该树的子树与另一颗子树是否相同,不断递归下去,只要相同就返回 true 。直到最后递归结束都没有匹配,则返回 false 。
5.2 代码实现判断是否为另一颗树的子树
class Solution {public boolean isSubtree(TreeNode root, TreeNode subRoot) {if(root == null) {return false;}if(isSameTree(root,subRoot)) {return true;}if(isSubtree(root.left,subRoot)) {return true;}if(isSubtree(root.right,subRoot)) {return true;}return false;}public boolean isSameTree(TreeNode p, TreeNode q) {if( p != null && q == null || p ==null && q != null) {return false;}if(p == null && q == null ){return true;}if(p.val != q.val) {return false;}return isSameTree(p.left, q.left) && isSameTree(p.right,q.right);} }



 —— 概念、SpringBoot + MyBatis(controller+service+mapper)开发流程与过程梳理)




)
)

)



)


)

)
补题)