个人主页:元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客
个人专栏:http://t.csdnimg.cn/ZxuNL
http://t.csdnimg.cn/c9twt
前言:这个专栏主要讲述递归递归、搜索与回溯算法,所以下面题目主要也是这些算法做的
我讲述题目会把讲解部分分为3个部分:
1、题目解析
2、算法原理思路讲解
3、代码实现
一、求根节点到叶节点数字之和
题目链接: 求根节点到叶节点数字之和
题目:
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
- 例如,从根节点到叶节点的路径
1 -> 2 -> 3表示数字123。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1:

输入:root = [1,2,3] 输出:25 解释: 从根到叶子节点路径1->2代表数字12从根到叶子节点路径1->3代表数字13因此,数字总和 = 12 + 13 =25
示例 2:
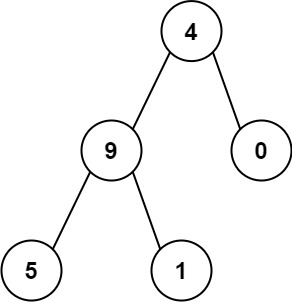
输入:root = [4,9,0,5,1] 输出:1026 解释: 从根到叶子节点路径4->9->5代表数字 495 从根到叶子节点路径4->9->1代表数字 491 从根到叶子节点路径4->0代表数字 40 因此,数字总和 = 495 + 491 + 40 =1026
提示:
- 树中节点的数目在范围
[1, 1000]内 0 <= Node.val <= 9- 树的深度不超过
10
二、解法
题目解析
这道题目的意思是:给我们一棵二叉树,让我们计算从根节点到叶节点生成的 所有数字之和 。
例如:
示例 :

从根到叶子节点路径 4->9->5 代表数字 495 从根到叶子节点路径 4->9->1 代表数字 491 从根到叶子节点路径 4->0 代表数字 40 因此,数字总和 = 495 + 491 + 40 = 1026
算法原理思路讲解
注意:我们在做递归这一类题目是要将递归看作一个黑盒,我们不管他是如何实现的,我们就相信他一定可以帮助我们完成目标
递归思路:
1、设计函数头(寻找重复子问题,并且将递归函数看作一个黑盒)。
2、设计函数体(只关心一个子问题,并解决它)
3、设计函数出口(递归的终止条件)
算法思路:
根据题目意思可得,我们可以使用一个前序遍历
在前序遍历的过程中,我们可以往左右⼦树传递信息,并且在回溯时得到左右⼦树的返回值。递归函数可以帮我们完成两件事:
把上面翻译一下就是
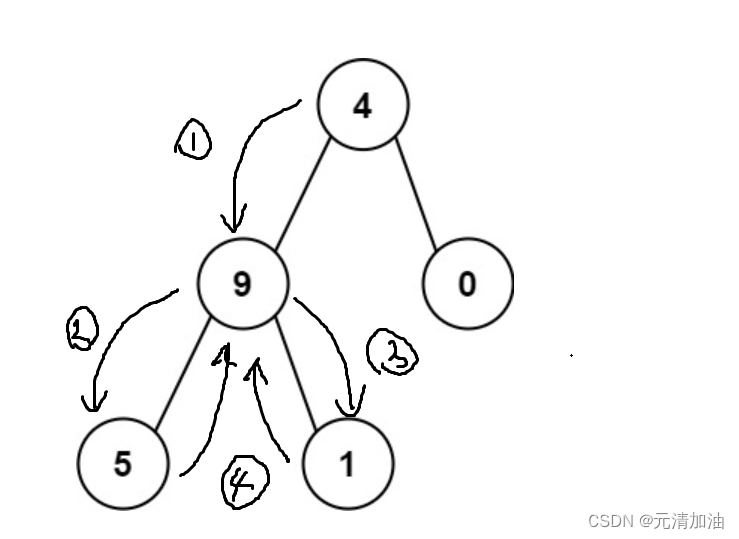
例如对于节点9来说
1、节点9将⽗节点的数字(4)与自己的数字9结合在一起成49传递到下一层
2、当遇到节点5的时候,就不再向下传递信息,⽽是将整合的结果(495)返回
 1、设计函数头
1、设计函数头
int dfs(TreeNode* root, int num)(1) 返回值:当前⼦树计算的结果(数字和)
(2)参数 num:递归过程中往下传递的信息(⽗节点的数字)
2、设计函数体(只关心一个子问题,并解决它)
- 当遇到空节点的时候,说明这条路从根节点开始没有分⽀,返回 0;
- 结合⽗节点传下的信息以及当前节点的 val,计算出当前节点数字 presum;
- 如果当前结点不是叶⼦节点,将 presum 传到左右⼦树中去,得到左右⼦树中节点路径的数字和,然后相加后返回结果。
presum = presum * 10 + root->val;int ret = 0;
if(root->left) ret += dfs(root->left, presum);
if(root->right) ret += dfs(root->right, presum);
return ret;3、设计函数出口
如果当前结点是叶⼦节点,直接返回整合后的结果 presum
if(root->left == nullptr && root->right == nullptr)return presum;以上思路就讲解完了,大家可以先自己先做一下
- 时间复杂度:O(n),其中 n 是二叉树的节点个数。对每个节点访问一次。
- 空间复杂度:O(n),其中 n 是二叉树的节点个数。空间复杂度主要取决于递归调用的栈空间,递归栈的深度等于二叉树的高度,最坏情况下,二叉树的高度等于节点个数,空间复杂度为 O(n)。
代码实现
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int dfs(TreeNode* root, int presum){presum = presum * 10 + root->val;if(root->left == nullptr && root->right == nullptr)return presum;int ret = 0;if(root->left) ret += dfs(root->left, presum);if(root->right) ret += dfs(root->right, presum);return ret;}int sumNumbers(TreeNode* root) {return dfs(root,0);}
};
)

)
补题)



|LeetCode503. 下一个更大元素 II、LeetCode42. 接雨水)

理解pod对象)

过大 转不了float 用Decimal)


)

![[Linux] 基于LAMP架构安装论坛](http://pic.xiahunao.cn/[Linux] 基于LAMP架构安装论坛)

