代码随想录算法训练营 --- 第五十九天

今天同样是单调栈，第二题很重要。

第一题：

简介：

本题可以说和上一题很是相似，只是有一点不同，数组是循环的。本题有两种巧妙地解法，都不难。

第一种方法（也是第一个想出来的方法）：

拼接数组，我们将两个相同的ｎｕｍｓ数组进行拼接这样我们就可以保证第一个ｎｕｍｓ数组进行了循环的遍历。此方法容易相处但是有很多弊端：例如浪费空间很多，也做了很多多余的操作，我们拼接数组后，还要剪切数组等等。

代码实现：

vector<int> nextGreaterElements(vector<int>& nums) {stack<int> str;vector<int> path(nums.size()*2,0);vector<int> result(nums.size()*2,-1);str.push(0);int k=0;for(int i=0;i<nums.size()*2;i++){if(k==nums.size()) k=0;path[i] = nums[k];k++;}for(int i=1;i<path.size();i++){if(path[i]>path[str.top()]){while(!str.empty()&&path[i]>path[str.top()]){result[str.top()] = path[i];str.pop();}str.push(i);}else if(path[i] == path[str.top()]){str.push(i);}else{str.push(i);}}for(int i=0;i<nums.size();i++){result.pop_back();}return result;}

第二种方法（很巧妙的实现了循环遍历数组）：

此种方法我们通过　［i％ｎｕｍｓ．ｓｉｚｅ（）］来实现我们重复遍历数组的目的。

代码实现：

 vector<int> nextGreaterElements(vector<int>& nums) {vector<int> result(nums.size(), -1);if (nums.size() == 0) return result;stack<int> st;st.push(0);for (int i = 1; i < nums.size() * 2; i++) { // 模拟遍历两边nums，注意一下都是用i % nums.size()来操作if (nums[i % nums.size()] < nums[st.top()]) st.push(i % nums.size());else if (nums[i % nums.size()] == nums[st.top()]) st.push(i % nums.size()); else {while (!st.empty() && nums[i % nums.size()] > nums[st.top()]) {result[st.top()] = nums[i % nums.size()];st.pop();}st.push(i % nums.size());}}return result;}

第二题：

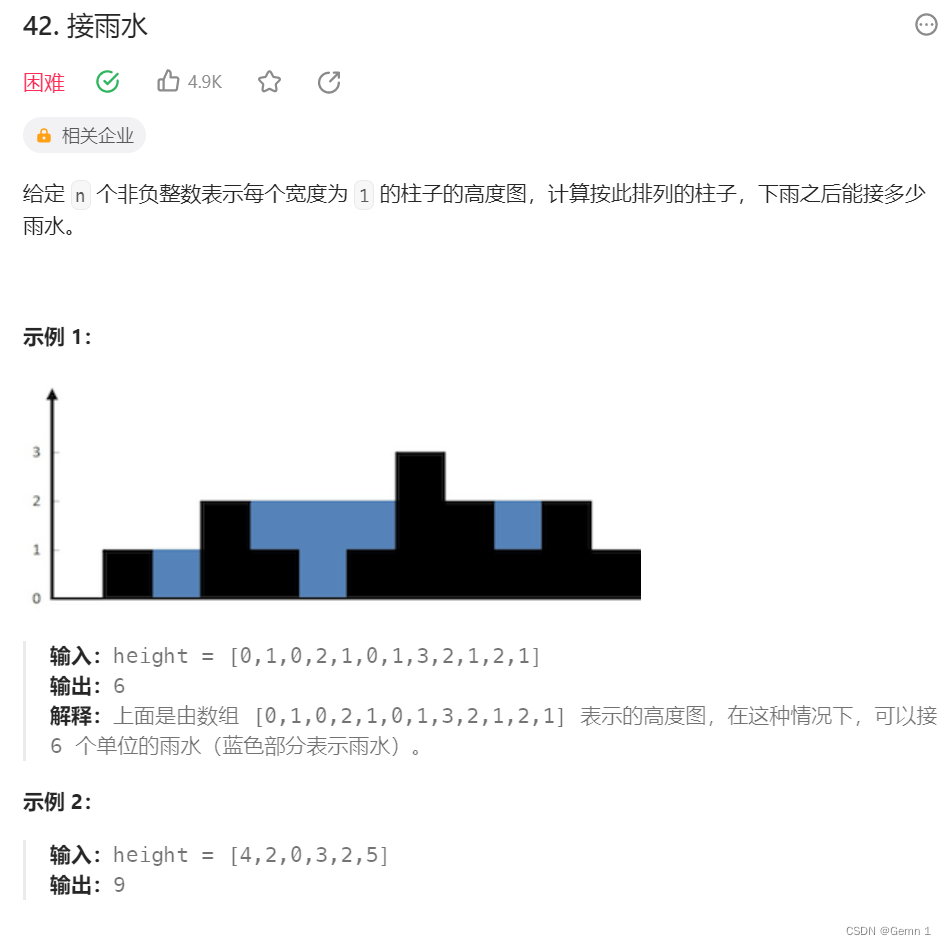
简介：

本题是面试中考的概率很高的一题。

本题共有三种方法

暴力破解法

暴力法的重点在于如何求出单列的水的体积例如：

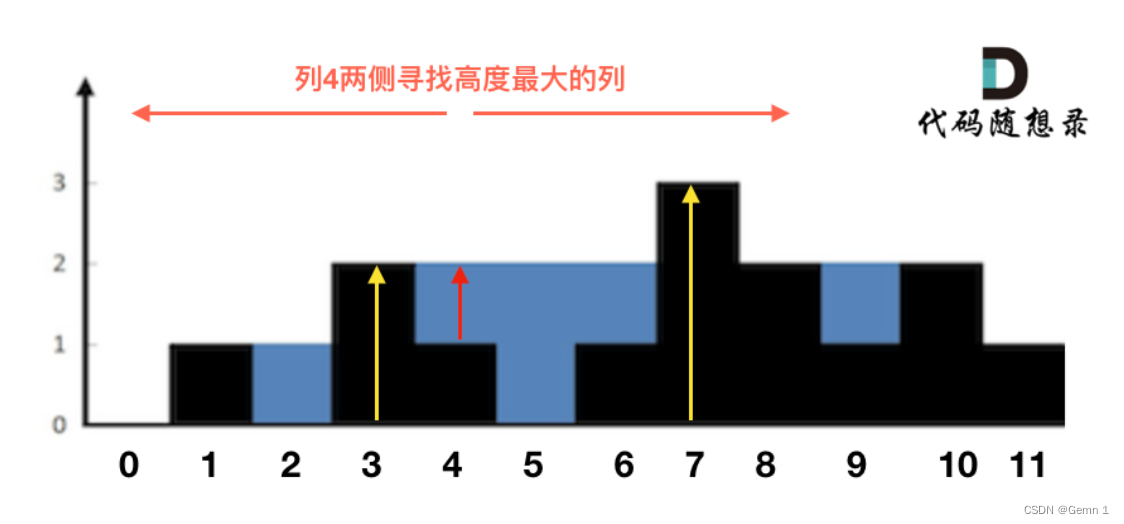
列4 左侧最高的柱子是列3，高度为2（以下用lHeight表示）。

列4 右侧最高的柱子是列7，高度为3（以下用rHeight表示）。

列4 柱子的高度为1（以下用height表示）

那么列4的雨水高度为列3和列7的高度最小值减列4高度，即： min(lHeight, rHeight) - height。

列4的雨水高度求出来了，宽度为1，相乘就是列4的雨水体积了。

此时求出了列4的雨水体积。

我们遍历每列然后将结果相加也就是最后的答案。

时间复杂度为O（ｎ）

代码实现：

 int trap(vector<int>& height) {int sum = 0;for (int i = 0; i < height.size(); i++) {// 第一个柱子和最后一个柱子不接雨水if (i == 0 || i == height.size() - 1) continue;int rHeight = height[i]; // 记录右边柱子的最高高度int lHeight = height[i]; // 记录左边柱子的最高高度for (int r = i + 1; r < height.size(); r++) {if (height[r] > rHeight) rHeight = height[r];}for (int l = i - 1; l >= 0; l--) {if (height[l] > lHeight) lHeight = height[l];}int h = min(lHeight, rHeight) - height[i];if (h > 0) sum += h;}return sum;}

双指针法

思路与暴力解法一样，只是我们在代码实现上有所不同，我们通过两个数组将左边柱子最大高度和右边柱子最大高度都记录下来。然后我们在遍历时就省下了很多时间。时间复杂度O（n）

代码实现：

  int trap(vector<int>& height) {if (height.size() <= 2) return 0;vector<int> maxLeft(height.size(), 0);vector<int> maxRight(height.size(), 0);int size = maxRight.size();// 记录每个柱子左边柱子最大高度maxLeft[0] = height[0];for (int i = 1; i < size; i++) {maxLeft[i] = max(height[i], maxLeft[i - 1]);}// 记录每个柱子右边柱子最大高度maxRight[size - 1] = height[size - 1];for (int i = size - 2; i >= 0; i--) {maxRight[i] = max(height[i], maxRight[i + 1]);}// 求和int sum = 0;for (int i = 0; i < size; i++) {int count = min(maxLeft[i], maxRight[i]) - height[i];if (count > 0) sum += count;}return sum;}

单调栈法

单调栈发与前两个解法不同，前两个解法是按列来计算，此解法为按行来计算。后面便利的过程建议去跟卡哥的视频走一趟就明白了，或者自己模拟过程。

代码实现：

  int trap(vector<int>& height) {if (height.size() <= 2) return 0; // 可以不加stack<int> st; // 存着下标，计算的时候用下标对应的柱子高度st.push(0);int sum = 0;for (int i = 1; i < height.size(); i++) {if (height[i] < height[st.top()]) {     // 情况一st.push(i);} if (height[i] == height[st.top()]) {  // 情况二st.pop(); // 其实这一句可以不加，效果是一样的，但处理相同的情况的思路却变了。st.push(i);} else {                                // 情况三while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是whileint mid = st.top();st.pop();if (!st.empty()) {int h = min(height[st.top()], height[i]) - height[mid];int w = i - st.top() - 1; // 注意减一，只求中间宽度sum += h * w;}}st.push(i);}}return sum;}