spring boot 事件机制

概述

spring boot 版本为 2.7.17 。

整体看一下spring及spring boot 相关事件。
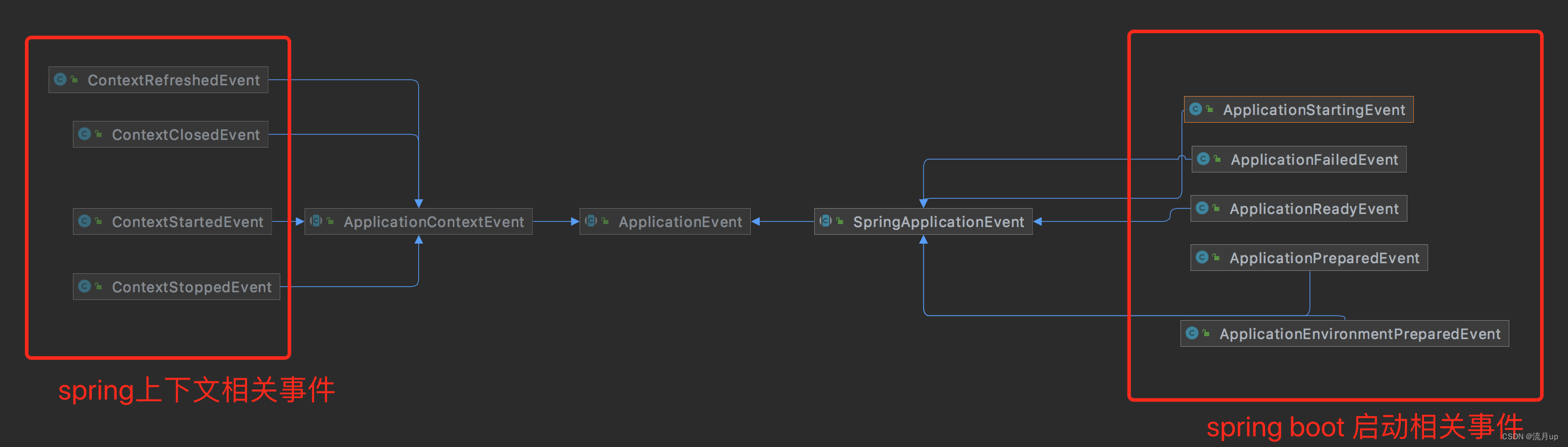
在这里插入图片描述

根据下文所给的源码关键处，打上断点，可以进行快速调试。降低源码阅读难度。

实践

spring 相关事件

上下文更新事件（ContextRefreshedEvent）：该事件会在ApplicationContext更新时发布。也可以在调用ConfigurableApplicationContext接口中的refresh()方法时被触发。
上下文开始事件（ContextStartedEvent）：当容器ConfigurableApplicationContext的Start()方法开始/重新开始容器时触发该事件。
上下文停止事件（ContextStoppedEvent）：当容ConfigurableApplicationContext的Stop()方法停止容器时触发该事件。
上下文关闭事件（ContextClosedEvent）：当ApplicationContext被关闭时触发该事件。容器被关闭时，其管理的所有单例Bean都被销毁。

spring boot 相关事件

ApplicationStartingEvent ：spring boot启动开始时执行的事件
ApplicationEnvironmentPreparedEvent：spring boot 对应Enviroment已经准备完毕，但此时上下文context还没有创建。
ApplicationPreparedEvent：spring boot上下文context创建完成，但此时spring中的bean是没有完全加载完成的(org.springframework.boot.SpringApplicationRunListeners#environmentPrepared 这个触发加载配置文件)。
ApplicationFailedEvent：spring boot启动异常时执行事件

监听spring boot ready事件

代码

@Component
public class SpringBootReadyListener implements ApplicationListener<ApplicationReadyEvent> {@Overridepublic void onApplicationEvent(ApplicationReadyEvent event) {System.out.println("....ready..");}
}

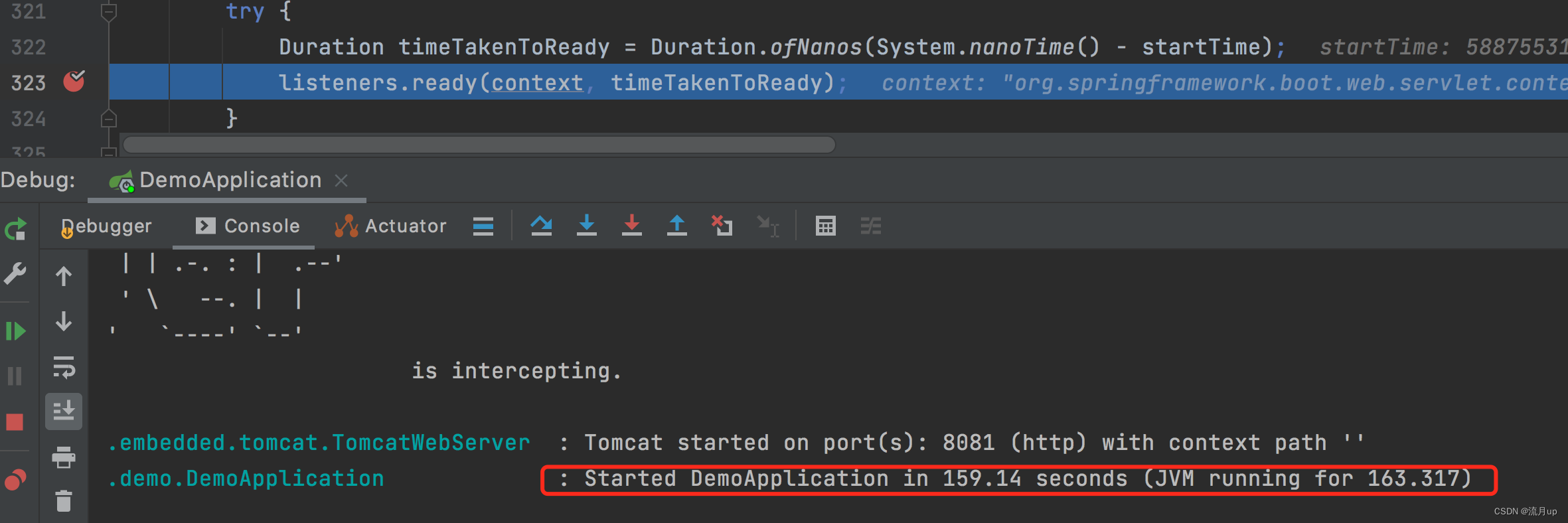
窗口执行结果
在这里插入图片描述

源码

初始化流程

org.springframework.boot.SpringApplicationRunListener 很重要的接口，后面spring boot 发事件消息，使用这个接口的实现类 org.springframework.boot.context.event.EventPublishingRunListener 来执行。

org.springframework.boot.SpringApplication#getRunListeners

在这里插入图片描述

调用流程

org.springframework.boot.SpringApplication#run(java.lang.Class<?>[], java.lang.String[])
org.springframework.boot.SpringApplication#run(java.lang.String...)
org.springframework.boot.SpringApplicationRunListeners#ready
org.springframework.boot.SpringApplicationRunListeners#doWithListeners(java.lang.String, java.util.function.Consumer<org.springframework.boot.SpringApplicationRunListener>, java.util.function.Consumer<org.springframework.core.metrics.StartupStep>)
org.springframework.boot.context.event.EventPublishingRunListener#ready
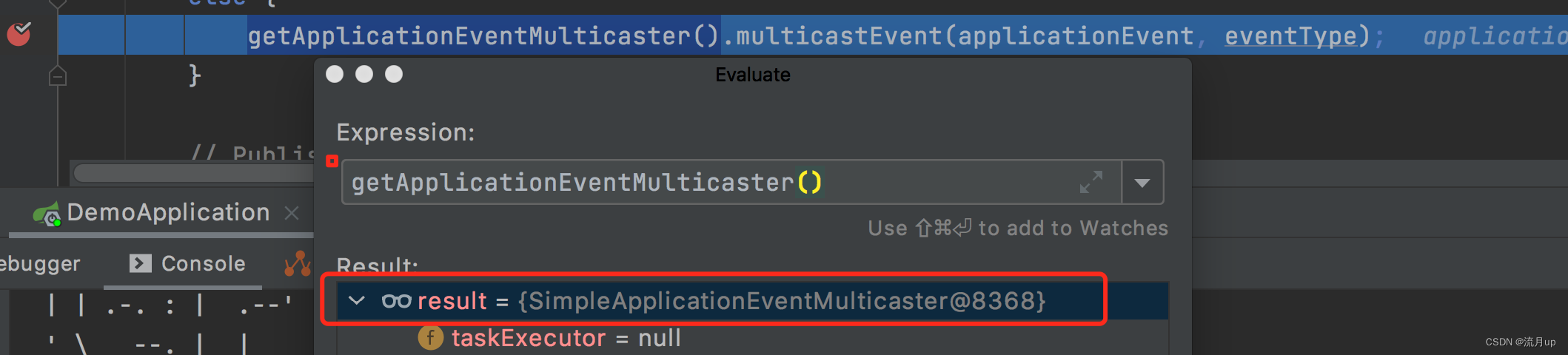
org.springframework.context.support.AbstractApplicationContext#publishEvent(java.lang.Object, org.springframework.core.ResolvableType)
org.springframework.context.support.AbstractApplicationContext#getApplicationEventMulticaster
org.springframework.context.event.SimpleApplicationEventMulticaster#invokeListener
org.springframework.context.event.SimpleApplicationEventMulticaster#doInvokeListener

在这里插入图片描述