从非结构化点云进行的曲面重建相当于生成一个合理的曲面，该曲面很好地近似于输入点。由于可能生成许多曲面，因此此问题不适合解决。已经提出了一系列广泛的方法来解决这个问题。其中包括变分方法、张量表决、隐式曲面和Delaunay三角剖分。

        对于基于Delaunay的算法，输出曲面通常生成为在输入点的3D Delaunay三角剖分中选择的一些三角形的并集。这样的算法要么是通过生成所选四面体的边界作为输出来基于体积的，要么是通过选择一组三角形来基于表面的。

        在大多数基于曲面的Delaunay算法中，三角形是独立选择的，即平行。

        本章介绍了一种基于曲面的Delaunay曲面重建算法，该算法依次选择三角形，也就是说，它使用先前选择的三角形来选择一个新的三角形来向前推进。在每一个前进步骤中，都会选择最合理的三角形，这样所选择的三角形会生成可定向的流形三角曲面。

        这种贪婪方法的另外两个例子是球旋转算法和Boyer-Petitjean算法。在这两种算法中，三角化曲面都是从种子三角形开始逐渐增长的。球的旋转很快，但重建的质量取决于与采样密度相对应的用户定义的参数。Boyer-Petitjean方法可以处理非均匀采样，但当遇到近共面点时失败，并且它不能对曲面的拓扑结构提供任何保证。

1、定义和算法

        该算法的第一步是构建点集的3D Delaunay三角剖分。三角形的半径rt是穿过三角形的顶点并且不包含任何样本点的最小球体的半径。换句话说，半径rt是从三角形的任何顶点到与该三角形对偶的Voronoi边的距离。这个具有三条边界边的三角形是初始三角剖分曲面，它的边界是推进前沿。半径最小的Delaunay三角形是贪婪算法的起点。

        该算法维护了一个候选三角形的优先级队列，即与当前曲面的边界边相交的有效三角形。优先级是合理性。当优先级队列不为空时，该算法从队列中弹出最合理的候选三角形并将其添加到曲面中。当前进前沿出现新的边界边时，新的候选三角形被推入优先级队列。由于该算法创建了一个双流形曲面，一些候选三角形由于拓扑约束而无法被选中，这将在下面解释。

1.1、拓扑约束

        任何被视为下一个潜在候选者的三角形t都与当前重建的前部共享一条边e。令b为与e相对的t的顶点。有四种配置可以将t添加到表面。

        如果b尚未在曲面上，则进行延伸。

        如果b在前面，并且b的两个邻居都在边缘e上，则进行孔填充。

        如果b在前面，并且b的前一个邻居在边缘e上，则进行耳部填充。

        如果b在前面，并且b的前面没有邻居在边缘e上，则进行粘合。

        虽然前三个操作从不引入非流形边或顶点，但如果三角形 t 有一个孪生面，即一个三角形有一条边在前面，与 b 相交，第三个顶点在边 e 上，我们只能执行粘合。

        当上述操作可以应用时，三角形是有效的。 

1.2、候选三角形的合理性

        对于前部边缘上的有效三角形，我们通过其半径进行比较。虽然半径在2D平滑曲线重建的情况下是一个很好的标准，但对于3D曲面重建，我们需要另一个标准，即表面上的三角形之间的二面角，也就是三角形法线之间的角度。有三个界限，即α银色、β和δ。

        边e的候选三角形是具有以下三个条件的三角形中半径最小的一个：对e是有效的；βt<α银色；与e相交的内部角度小于δ。

        可能没有这样的三角形。在算法的实现中，α银色和δ等于5π/6。

        我们用βt表示与边界边e相交的三角形t的法线与表面上与e相交的三角形的法线之间的角度。

        我们将可信度等级p(t)定义为1/rt，如果βt<β，否则为-βt。参数β可由用户指定，默认设置为π/6。

        让我们看一下下面的图。

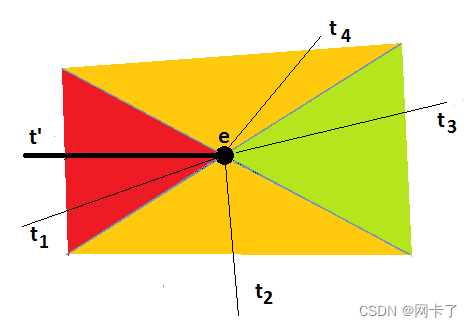
        α银色部分对应于红色楔形。即使t1是唯一的候选三角形，该算法也永远不会选择它。

        β对应于绿色楔形。如果此区域有候选三角形，则半径最小的三角形最有可能被选中。

        如果没有绿色楔形中的候选三角形，则选择其法线与t'法线之间夹角最小的三角形。在上面的图中，这将选择三角形t4。 

1.3、处理多个组件、边界和锐边

        通过构造，算法的输出是一个有或没有边界的连通定向流形。为了处理多个组件，我们只需在与曲面不相交的面上寻找一个新的种子面。在有噪声数据或异常值的情况下，用户必须过滤掉小的曲面组件。

        不可能同时处理各种边界和不均匀采样，因为空隙可能是表面采样不足的区域，也可能是孔洞。

        由于我们不希望算法依赖于采样的一致性条件，它将填补从表面“平坦”区域切出的孔洞。然而，在许多情况下，通过添加跨越圆盘无法闭合边界组件，因此得到的圆盘无法很好地采样。

        通常，由于操作的横向剪切而闭合边界组件，会在边界边缘产生较大的二面角。此外，如果边界被充分采样，则入射到边界边缘的两个三角形的半径将非常不同。这些启发式事实可用于边界检测。

        更具体地说，对于p(t)<0且rt>radius_ratio_bound×rt′的边e，我们丢弃任何候选三角形t，其中t′是表面上的三角形，与e相交。参数radius_ratio_bound由用户指定，默认设置为5。

        对于上图中给出的例子，我们说如果在绿色楔形中没有三角形t3，则三角形t4将被选择，因为它在其法线和三角形t'的法线之间具有最小的角度。然而，如果它的半径是三角形t'的半径的radius_ratio_bound倍，则三角形t2将被选择，假设它的半径不是radius_ratio_bound倍。

        请注意，这种启发式方法意味着，如果采样相对于曲率过于稀疏，则必须足够均匀，以便我们的算法能够工作。