今天这篇文章是接上一篇文章的，主要讲述的是获取SW设计结构树节点的第二种方法。

这个方法获取节点的逻辑是先获取最顶层节点，然后再通过获取顶层节点的子节点一层一层的把所有节点都找出来，也就是需要递归。想要用这个方法就要了解下面几个API。

其中第一个API如下所示：

GetRootComponent3 Method (IConfiguration)

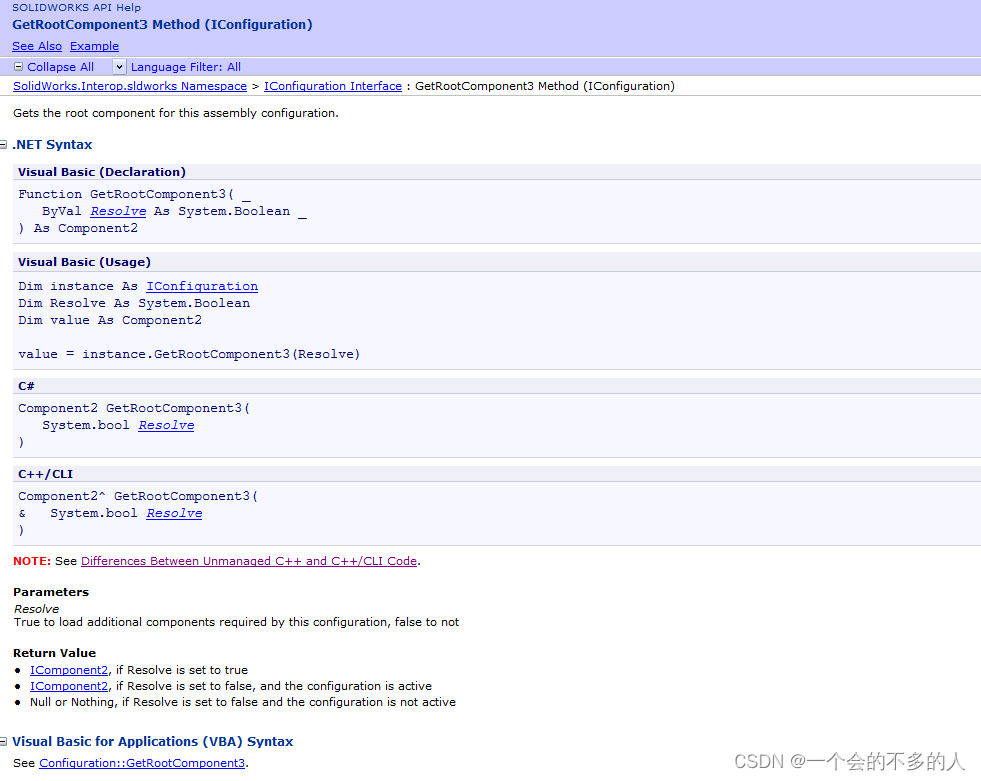
上述API解释是：获取此程序集配置的根组件

下面是这个方法的使用例子：

        public void Main(){ModelDoc2 swModel;ConfigurationManager swConfMgr;Configuration swConf;Component2 swRootComp;swModel = (ModelDoc2)swApp.ActiveDoc;swConfMgr = (ConfigurationManager)swModel.ConfigurationManager;swConf = (Configuration)swConfMgr.ActiveConfiguration;swRootComp = (Component2)swConf.GetRootComponent();System.Diagnostics.Stopwatch myStopwatch = new Stopwatch();myStopwatch.Start();Debug.Print("File = " + swModel.GetPathName());TraverseModelFeatures(swModel, 1);if (swModel.GetType() == (int)swDocumentTypes_e.swDocASSEMBLY){TraverseComponent(swRootComp, 1);}myStopwatch.Stop();TimeSpan myTimespan = myStopwatch.Elapsed;Debug.Print("Time = " + myTimespan.TotalSeconds + " sec");}第二个API是GetChildren Method (IComponent2)

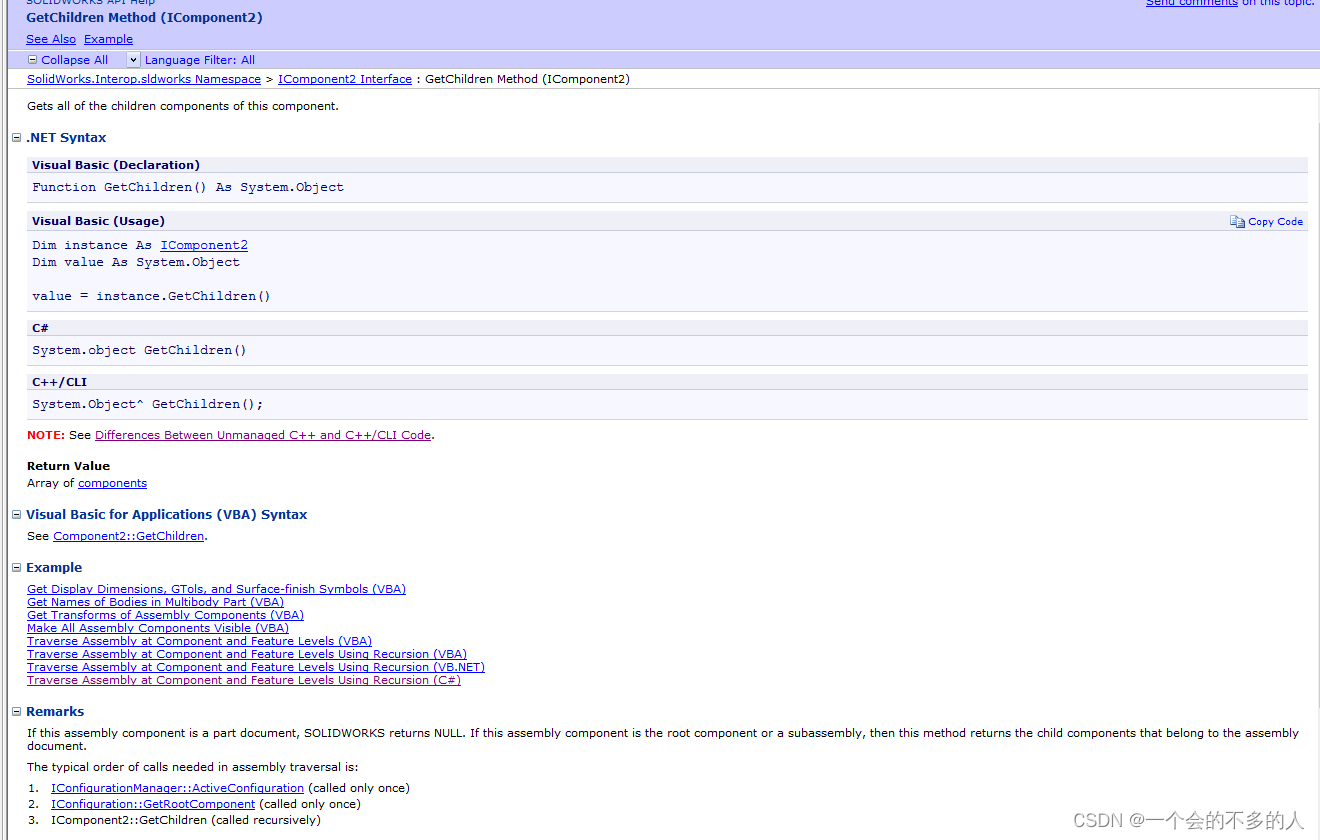
方法的解释是：获取此组件的所有子组件。

所以通过上面两个API的结合，我们也可以获取所有我们想要的节点信息。

今天这篇文章就介绍这么多，我们下篇文章再见。