games101的第四节课讲了三维变换和观察变换,我们这里先记录一下三维变换的知识,后面再讲观察变换
齐次坐标下的三维变换
类似于解决之前二维变换平移的问题,三维变换下用齐次坐标通过增加一个维度来表示,第四个维度为1表示这是个点,第四个维度为0表示这是个向量,这样就可以通过四维矩阵乘法来表示平移变换了

这样,所有的三维变换就可以通过一个矩阵乘法来表示了

和之前二维变换类似的,三维下的缩放和平移都可以用类似的矩阵表示

比较复杂的是三维中的旋转,二维中的旋转方式是固定的,要么是逆时针旋转要么是顺时针旋转
但是在三维中旋转的角度可以是任意方向的,如何用一个变换矩阵来表示呢
首先从简单的x、y和z三个轴方向上的旋转来研究
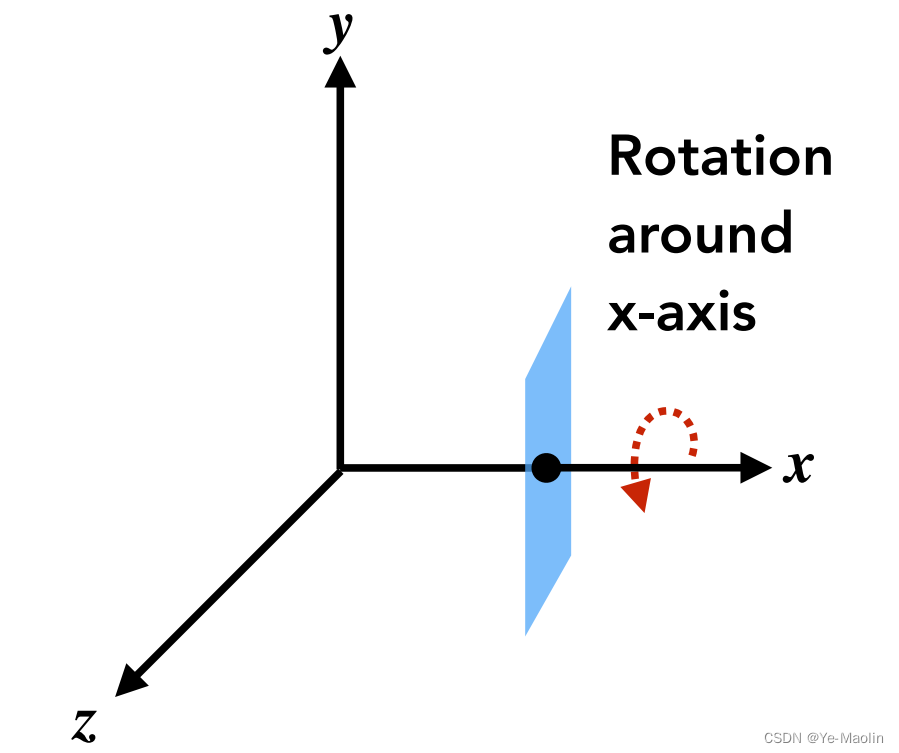
如果是绕着x轴旋转,那么就是x坐标不变,y和z坐标在发生变化,类似于二维的旋转矩阵表示
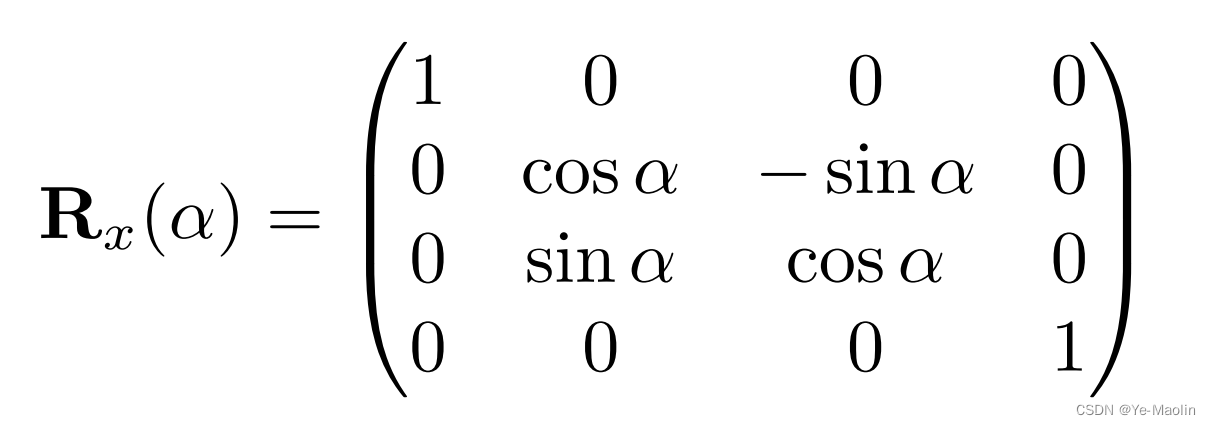
如果是绕着z轴旋转,那么就是z坐标不变,x和y坐标在发生变化,类似于二维的旋转矩阵表示
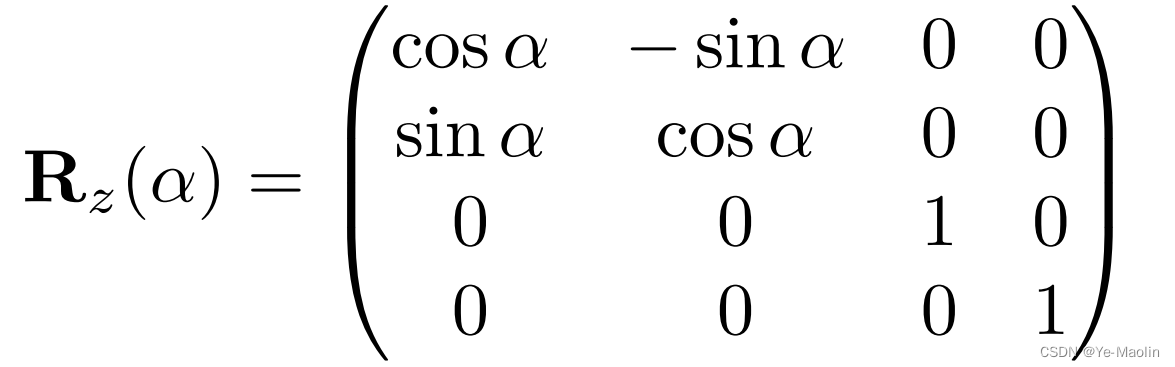
但是到了绕着y轴旋转时,实际的旋转矩阵是这样的

你可能会发现,之前正弦值都是右上角的是负的,为什么到了绕y轴旋转时,却变成了左下角是负的呢?
如何来理解这个事情,我们知道x和y叉乘可以得到z,y和z叉乘可以得到x,但是呢,x和z叉乘得到的是-y,只有z和x叉乘得到的才是y,所以呢,到了旋转的时候,实际上是整个的角度取反了,余弦函数是偶函数,所以没变化,但是正弦函数是奇函数,符号就发生了变化
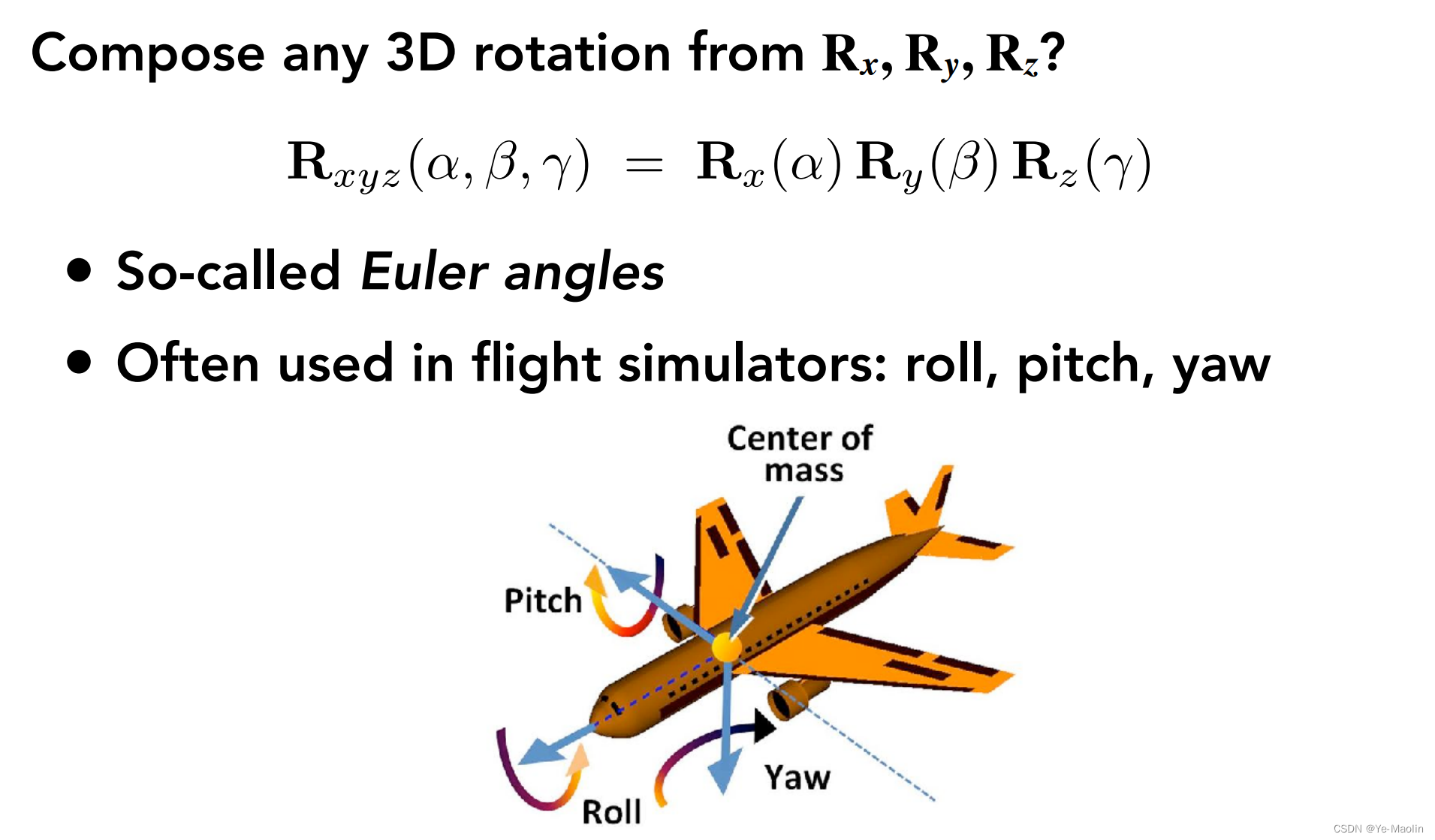
现在呢我们知道了在三个轴上的旋转如何变换了,那么对于任意角度的旋转,实际上就可以通过在这三个轴上的旋转合成来实现,这一组角,就叫做欧拉角,好比飞机的俯仰pitch、偏航yaw和翻转roll
现在问题是如何用一个统一的矩阵变换来表示三维空间的旋转,实际上对于任意方向的旋转都可以表示为相对于某个方向的旋转轴旋转,这里引入罗德里德斯的旋转公式,可以根据旋转轴n和对应的旋转角度来完成任意方向的旋转




3D Gaussian Splatting Instant-NGP)


创建actor)









![二叉树的层平均值[中等]](http://pic.xiahunao.cn/二叉树的层平均值[中等])


