问题描述
“六度空间”理论又称作“六度分隔(Six Degrees of Separation)”理论。这个理论 可以通俗地阐述为:“你和任何一个陌生人之间所间隔的人不会超过六个，也就是 说，最多通过五个人你就能够认识任何一个陌生人。”假如给你一个社交网络图， 请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。 输入要求 多组数据，每组数据 m+1 行。第一行有两个数字 n 和 m，代表有 n 个人和 m 组朋友关系。n 个人的编号为 1 到 n。第二行到第 m+1 行每行包括两个数字 a 和 b，代表这两个人互相认识。当 n 和 m 都等于 0 时，输入结束。 输出要求 每组数据输出 n 行，对每个结点输出与该结点距离不超过 6 的结点数占结点 总数的百分比，精确到小数点后 2 位。每个结节点输出一行，格式为“结点编号:(空 格)百分比%”
运行结果：
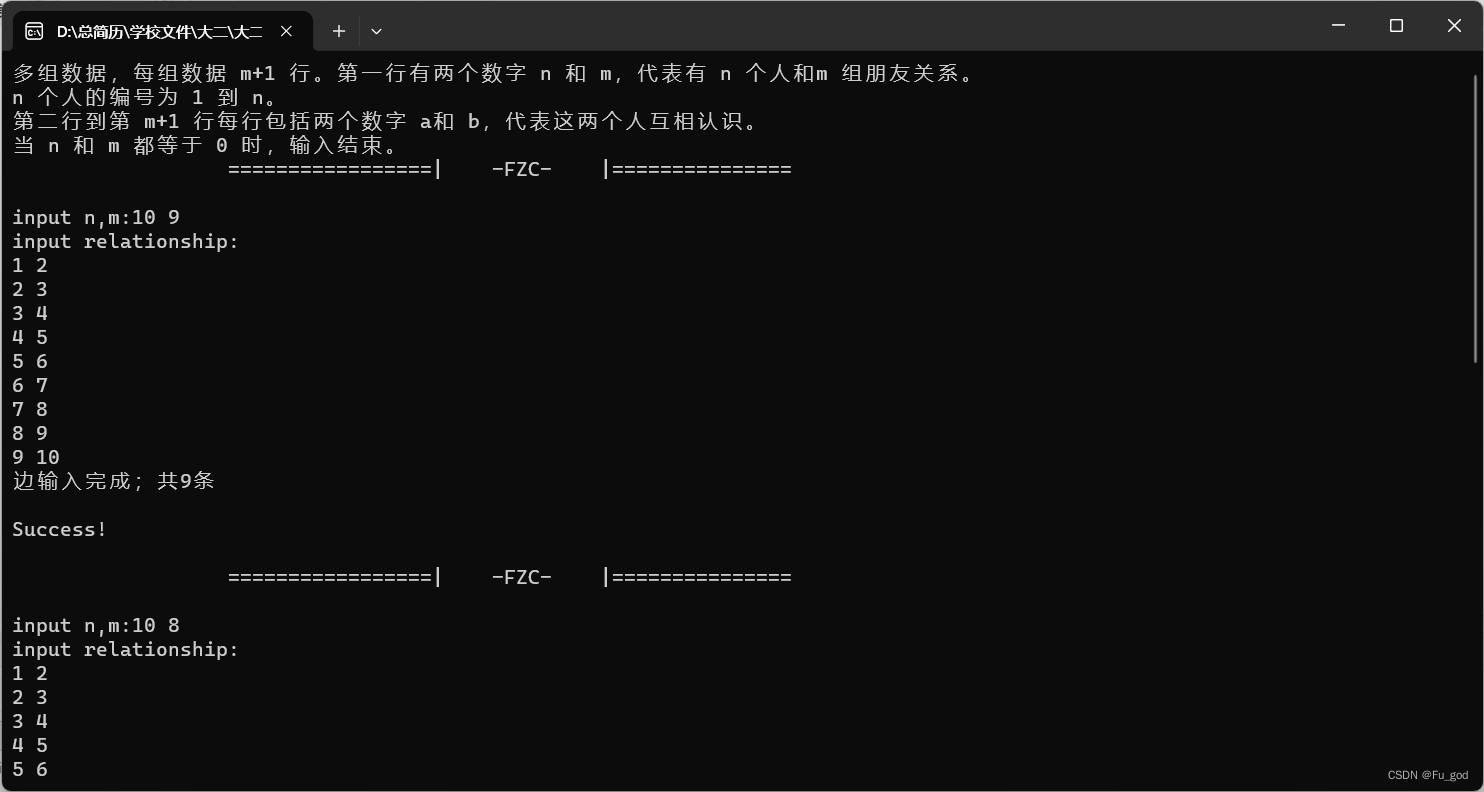
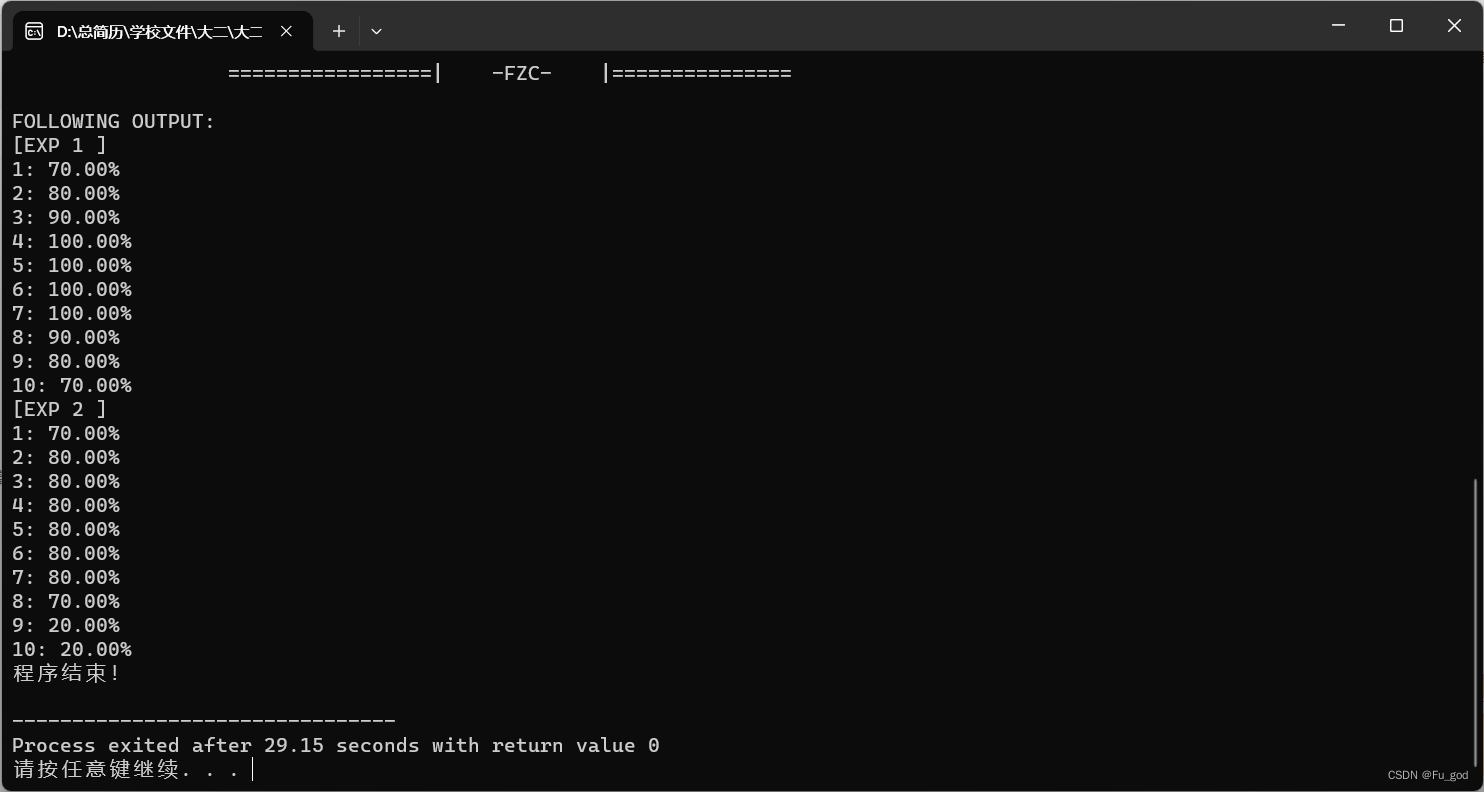
代码实现：
#include <stdio.h>
#include <stdlib.h>
#define MaxS 20
#define MaxE 5
//结构体部分
typedef struct{ //图结构体定义 char vex[MaxS]; //顶点数组 int vexnum; //顶点个数 int mat[MaxS][MaxS]; //邻接矩阵 int arcnum; //边数
}Graph;
typedef struct{int head,tail;int mat[20]; //队列数组
}Queue;
//全局变量部分
float result[MaxE][MaxS]; //结果存储函数
int cunt; //用于全局变量遍历
int state[MaxS];
//函数声明部分
void Init(Graph *a);
int Read(Graph *a);
void Cal(Graph *a);
void show();
float BFS(Graph *a,int s);
void InitQ(Queue *q); //初始化队列
void push(Queue* q,int n); //入队
int pop(Queue *q); //出队
//函数定义部分
void InitQ(Queue *q){q->head=0;q->tail=0;
}
void push(Queue* q,int n){q->mat[q->tail] = n;q->tail++;
}
int pop(Queue* q){q->head++;if(q->head>q->tail)return -1;return q->mat[q->head-1];
}
float BFS(Graph *a,int s){int tmp,rs=0;int *len=(int*)malloc(sizeof(int)*a->vexnum+1); //记录到s的距离 for(int i=0;i<=a->vexnum;i++){state[i] = 0;len[i] = 0;}Queue* q = (Queue*)malloc(sizeof(Queue));InitQ(q);push(q,s);state[s]=1;for(int i = 0;i<a->vexnum;i++){ //总共遍历a->vexnum次tmp = pop(q);if(tmp==-1)continue;for(int j=1;j<=a->vexnum;j++){ //每次扫描vexnum个数 if(a->mat[tmp][j]==1&&state[j]==0){len[j] = len[tmp]+1;state[j] = 1; //状态变成已访问push(q,j);continue;}}}for(int i=1;i<=a->vexnum;i++){if(len[i]<=6&&len[i]!=0)rs+=1;}for(int i=1;i<=a->vexnum;i++){}free(len);free(q);return (float)(rs+1)/a->vexnum*100;
}
void show(){printf("\n =================| -FZC- |=============== \n\n"); printf("FOLLOWING OUTPUT:\n");for(int i=0;i<cunt;i++){printf("[EXP %d ]\n",i+1);for(int j=1;j<MaxS;j++){if(result[i][j]==-1)break;printf("%d: %.2f%%\n",j,result[i][j]);}}
}
void Init(Graph *a){a->arcnum=0;a->vexnum=0;for(int i=0;i<MaxS;i++){a->vex[i] =0;state[i] = 0;result[cunt][i] = -1;for(int j=0;j<MaxS;j++){a->mat[i][j] = 0;}}}int Read(Graph *a){int n,m,s,e;printf("input n,m:");scanf("%d %d",&n,&m);if(n==0&&m==0)return 1; //若均为0则返回1 a->vexnum = n;a->arcnum = m;printf("input relationship:\n");for(int i=0;i<m;i++){scanf("%d %d",&s,&e);a->mat[s][e] = 1;a->mat[e][s] = 1; }printf("边输入完成；共%d条\n",a->arcnum);return 0;
}
void Cal(Graph *a){for(int i=1;i<=a->vexnum;i++){result[cunt][i] = BFS(a,i);}printf("\nSuccess!\n");cunt++;
}
//主函数部分
int main(){int flag = 0; Graph* a=(Graph*)malloc(sizeof(Graph));cunt=0;printf("多组数据，每组数据 m+1 行。第一行有两个数字 n 和 m，代表有 n 个人和m 组朋友关系。\nn 个人的编号为 1 到 n。\n第二行到第 m+1 行每行包括两个数字 a和 b，代表这两个人互相认识。\n当 n 和 m 都等于 0 时，输入结束。");while(1){//初始化Init(a);printf("\n =================| -FZC- |=============== \n\n");//读取数据flag = Read(a);if(flag==1){show(); //输出结果break; }//处理数据Cal(a); }printf("程序结束！\n"); return 0;
}
