个人主页：元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客
个人专栏：http://t.csdnimg.cn/ZxuNL
http://t.csdnimg.cn/c9twt
前言：这个专栏主要讲述递归递归、搜索与回溯算法，所以下面题目主要也是这些算法做的
我讲述题目会把讲解部分分为3个部分：
1、题目解析
2、算法原理思路讲解
3、代码实现
一、计算布尔二叉树的值
题目链接：计算布尔二叉树的值
题目：
给你一棵 完整二叉树 的根，这棵树有以下特征：
- 叶子节点 要么值为
0要么值为1，其中0表示False，1表示True。 - 非叶子节点 要么值为
2要么值为3，其中2表示逻辑或OR，3表示逻辑与AND。
计算 一个节点的值方式如下：
- 如果节点是个叶子节点，那么节点的 值 为它本身，即
True或者False。 - 否则，计算 两个孩子的节点值，然后将该节点的运算符对两个孩子值进行 运算 。
返回根节点 root 的布尔运算值。
完整二叉树 是每个节点有 0 个或者 2 个孩子的二叉树。
叶子节点 是没有孩子的节点。
示例 1：
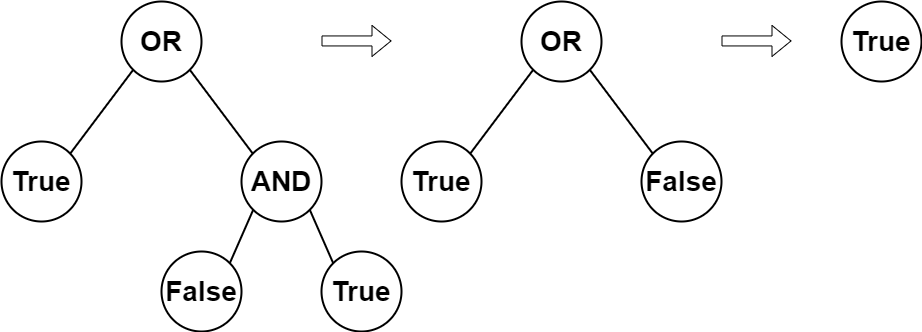
输入：root = [2,1,3,null,null,0,1] 输出：true 解释：上图展示了计算过程。 AND 与运算节点的值为 False AND True = False 。 OR 运算节点的值为 True OR False = True 。 根节点的值为 True ，所以我们返回 true 。
示例 2：
输入：root = [0] 输出：false 解释：根节点是叶子节点，且值为 false，所以我们返回 false 。
提示：
- 树中节点数目在
[1, 1000]之间。 0 <= Node.val <= 3- 每个节点的孩子数为
0或2。 - 叶子节点的值为
0或1。 - 非叶子节点的值为
2或3。
二、解法
题目解析
这道题目的意思：
1、叶子节点 要么值为 0 要么值为 1 ，其中 0 表示 False ，1 表示 True 。
2、非叶子节点 要么值为 2 要么值为 3 ，其中 2 表示逻辑或 OR（||） ，3 表示逻辑与 AND （&&）
那么这道题的意思，就是先将两个叶子节点中的布尔值与他们的父亲节点的逻辑运算符计算
如下图：
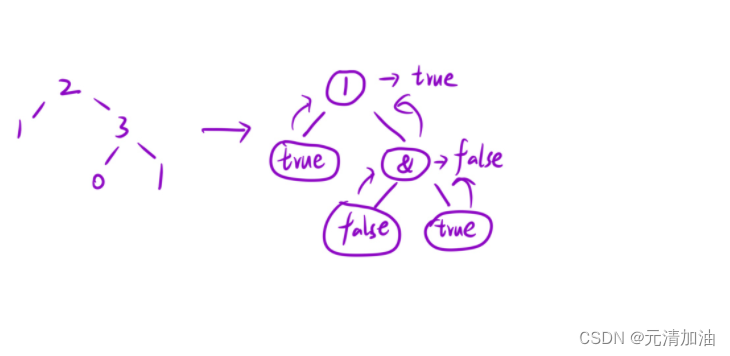
算法原理思路讲解
注意：我们在做递归这一类题目是要将递归看作一个黑盒，我们不管他是如何实现的，我们就相信他一定可以帮助我们完成目标
递归思路：
1、设计函数头（寻找重复子问题，并且将递归函数看作一个黑盒）。
2、设计函数体（只关心一个子问题，并解决它）
3、设计函数出口（递归的终止条件）
算法思路：
根据题目意思可得，我们先要遍历到两个叶子节点，再到他们的父亲节点。我们一看到这里，我们应该就可以立刻想到使用一个后序遍历即可解决
1、设计函数头
我们可以设计一个递归函数，参数是一个树的根，返回计算后的布尔值
bool dfs(TreeNode* root);2、设计函数体（只关心一个子问题，并解决它）
（1）求出左子树的布尔值
（2）求出右子树的布尔值
（3）利用左右子树的布尔值求出最后返回的布尔值
bool left = dfs(root->left);
bool right = dfs(root->right);
return root->val == 2 ? left || right : left && right;3、设计函数出口
当他左右子树为空时，就可以返回他本身的布尔值了。
if (root->left == nullptr){return root->val == 0 ? false : true;}以上思路就讲解完了，大家可以先自己先做一下
- 时间复杂度：O(n)，其中 n 表示树中节点的数目。对于每个节点我们只需遍历一次即可，因此时间复杂度为 O(n)。
- 空间复杂度：O(n)，其中 n 表示树中节点的数目。按照题目要求，含有 n 个节点的完整二叉树的深度最多为 n/2 ，最少为 O(logn)，因此递归的最大深度为 n/2，因此空间复杂度为O(n)。
代码实现
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool evaluateTree(TreeNode* root) {if (root->left == nullptr){return root->val == 0 ? false : true;}bool left = evaluateTree(root->left);bool right = evaluateTree(root->right);return root->val == 2 ? left || right : left && right;}
};
