题目地址：有效三角形的个数

---

解决此题时，首先需要知道的是如何判断三个数字是否能够构成三角形。

我们知道，三角形任意两边之和都大于第三边。所以判断三个数字是否能构成三角形需要进行三次比较（最基础的思路）

方法一：暴力枚举

此题一个最容易想到的解法就是暴力遍历。即穷举法，列举出每一种可能的组合情况并进行判断。不难想到需要设置三重循环，时间复杂度是O(n^3)。但是这种方法可能会有超时的风险（也许使用C/C++能够侥幸通过，但如果使用python之类较慢的语言大概率无法通过）

方法二：双指针

上述我们已经给出了判断三个数是否构成三角形的方法，然而三次判断其实也比较繁琐，是否可以实现一次判断呢？

其实我们在数学学习中肯定知道一种方法，那就是判断三个数中较小的两个数之和与最大数的大小关系。因为只要最小的数加起来大于最大的数，那么这三个数无论如何组合，最后得到的结果肯定都是满足三角形的性质的。

因此我们就可以采取这样一种思想来设计算法。首先找到最大的数，然后对于剩余的数进行排列组合，判断它们的和是否大于最大的数。

为了找到最大的数，我们可以先将原数组进行升序排序。此时可以知道最大的数就在数组尾端。此时设置双指针，分别指向剩余数组中的最小数与最大数。通过操作双指针进行判断。

如何控制双指针的指向呢？我们可以以下列例子来简单模拟一下：

 

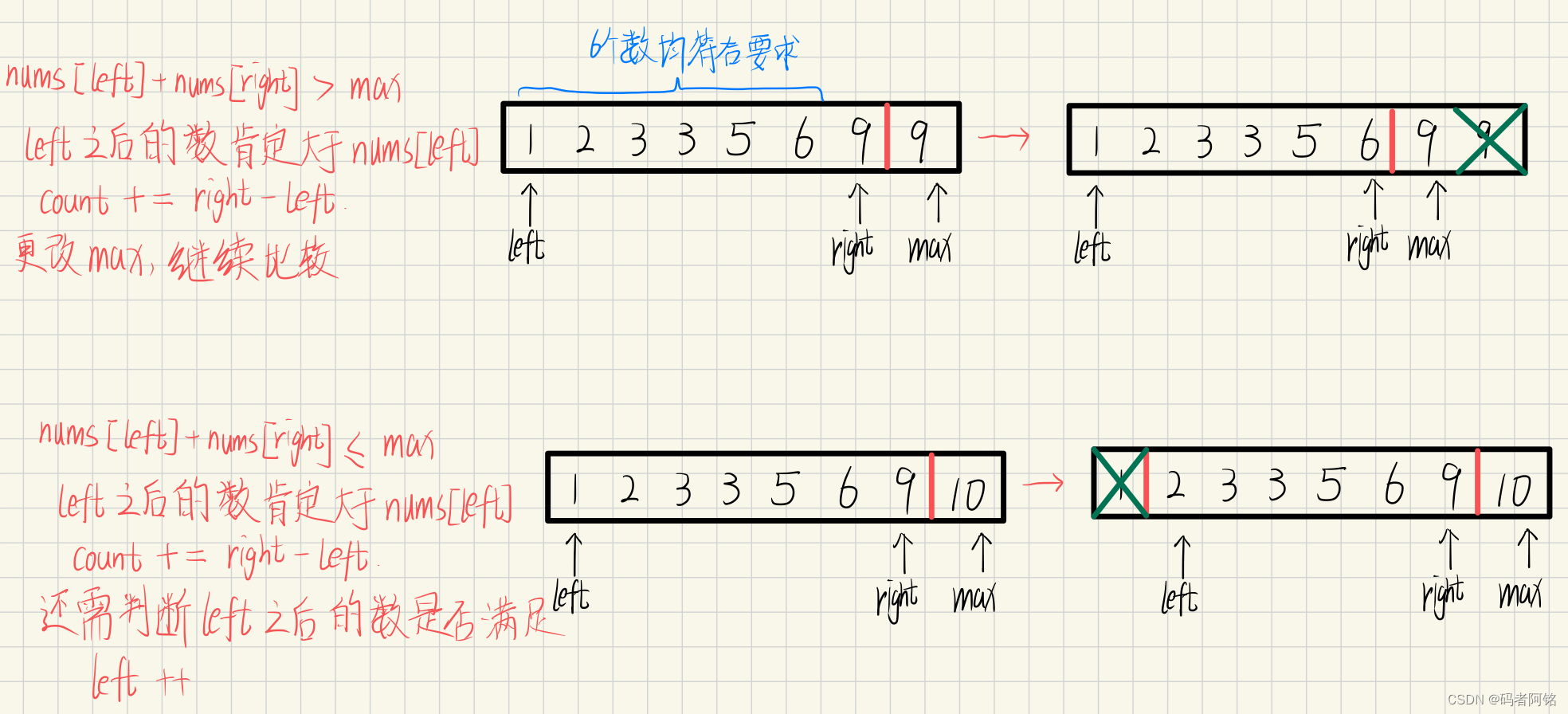
需要注意的是，max至少需要指向第三个元素（下标为2），因为至少需要三条边才能构成一个三角形。

采用双指针方法时间复杂度为O(n^2)，相较于暴力解法有很大提升。

class Solution {
public:int triangleNumber(vector<int>& nums) {sort(nums.begin(),nums.end());int ret=0;int n=nums.size();for(int i=n-1;i>=2;i--){int left=0,right=i-1;while(left<right){if(nums[left]+nums[right]>nums[i]){ret+=right-left;right--;}else{left++;}}}return ret;}
};