稳住心态不要慌,如果考试周冲突的话,可以直接复制这篇博客和上一篇博客西工大计算机学院计算机系统基础实验一(函数编写1~10)-CSDN博客最后的代码,然后直接提交,等熬过考试周之后回过头再慢慢做也可以。
第11个函数,rempwr2,要求计算x%(2^n),其中0<=n<=30。比如rempwr2(15,2) = 3, rempwr2(-35,3) = -3。什么意思呢?意思是15%(2^2)=15%4=3,-35%(2^3)=-35%8=-3。那么我们该怎么做呢?先考虑正数,当x为15并且n为2时,15可写作1111B,15%(2^2)即相当于取1111B的低2个比特位,即11B,正如答案中的3。接着考虑负数,-35可写作0xFFFF FFFF FFFF FFDD,-3可写作0xFFFF FFFF FFFF FFFD,如果像处理正数那样直接截取0xFFFF FFFF FFFF FFDD的第3个比特位的话,得到的应该是101B,也就是5,而不是-3,所以负数不能像正数那样被处理。最简单的方法是分类讨论,但是那样会使用蛮多的运算符,所以尝试使用一种新的思路去处理这个问题。我们可不可以这样子,先计算35%(2^3)=3,然后再把3变为-3呢?也就是说,先把一个数变成它自己的绝对值,然后参与%运算,最后再根据最开始这个数的符号位调整最终的结果呢?按照这个思路,我们首先将x变成它的绝对值,可以通过(x+(x>>31))^(x>>31)来实现,当为正时,(x+(x>>31))^(x>>31)的结果仍为x,当x为负数时,比如x=-35=0xFFFF FFDD,那么x>>31=0xFFFF FFFF,x+(x>>31)的结果是0xFFFF FFDE,接着0xFFFF FFDE与0xFFFF FFFF异或,得到了0x0000 0023,也就是35。(当x为负数时,+(x>>31)相当于-1,接着与x>>31异或相当于全取反,就是根据负数原码求补码的逆过程,只不过考虑到表达式(x+(x>>31))^(x>>31)也综合了x是正数的情况,所以不方便直白的写减一后全取反)接着当n=2时如何产生0000... ...0011,当n=3时如何产生0000... ...0111呢?可以通过(~0)+(1<<n)来产生。~0为0xFFFF FFFF,当n=3时,1<<3为0x8,~0+(1<<3)即得到了0x0000 0007。这时让((x+(x>>31))^(x>>31))与~0+(1<<n)进行位与操作,即可完成%操作。此时若x是正数,则所有步骤已完成,但是当x为负数时,还需要将最后的结果加一个负号。怎么加负号呢?各位取反加1,先与x>>31做异或操作完成各位取反,最后减去x>>31完成加1。结合上述的讲解,我们给出代码,如 图1:编写第11个函数rempwr2 所示。接着仿照前10个函数相同的检查流程,如 图2:检查第11个函数rempwr2 所示。
int s = x>>31;
x = (x+s)^s;
x &= ((~0)+(1<<n));
return (x^s)+~s+1;(图1:编写第11个函数rempwr2)


(图2:检查第11个函数rempwr2)
第12个函数,satMul2,执行算术乘法乘2。怎么做呢?如果x为小于0x4000 0000的正数,或者为0,或者为大于C000 0000的负数,那么直接返回x<<1即可。而当x超出这个范围时,就不能直接返回x<<1了。那如何判断什么时候可以直接返回x<<1,什么时候不能直接返回x<<1呢?发现可以引入变量int x2=x<<1,x2表示x*2,再引入变量int sx2=(x2)>>31表示x*2的符号位,一旦x的符号位与x<<1的符号位不相同,即(x^x2)>>31的结果为0xFFFF FFFF时,就不能直接返回x<<1,而如果x的符号位与x<<1的符号位相同,即(x^x2)>>31的结果为0x0时,就可以直接返回x<<1,所以可以引入变量int flag=(x^x2)>>31,并以此作为判断条件。根据已有的知识,可以写出下面的大框架:
(flag&( )) | (~flag&( x2 ))
接着,如果x的符号位与x<<1的符号位不相同,即(x^x2)>>31的结果为0xFFFF FFFF,不能直接返回x<<1时,该返回什么呢?易知此时只需返回0x8000 0000或者0x7FFF FFFF。该如何得知该返回0x8000 0000还是该返回0x7FFF FFFF呢?发现这时当x为很大的正数,并且x2的符号位为1时,sx2为0xFFFF FFFF,加上0x8000 0000之后即为0x7FFF FFFF,即应该返回的值;当x为很小的负数,并且x2的符号位为0时,sx2为0x0000 0000,加上0x8000 0000之后即为0x8000 0000,即应该返回的值。而0x8000 0000可写作1<<31。根据这个分析,我们进一步完善大框架:
(flag&( sx2+(1<<31) )) | (~flag&( x2 ))
这时再思考,能不能想办法进行优化以减少运算符使用的个数呢?发现当flag为0xFFFF FFFF时,(~flag&( x2 )中的x2不一定一定为0;当~flag为0xFFFF FFFF时,(flag&( sx2+(1<<31) ))中的sx2+(1<<31)也不一定一定为0,所以不能像第9个函数那样进行优化。因此,第12题最终的代码为如 图3:编写第12个函数satMul2 所示。
int x2=x<<1;int sx2=x2>>31;int flag=(x^x2)>>31;int tmin=1<<31;return ((~flag&x2)+(flag&(sx2+tmin)));(图3:编写第12个函数satMul2)
然而这道题似乎有问题。为什么呢?其实只要简单的"return x<<1"就能通过!白白耗费我们这么多时间。如 图4:检查第12个函数satMul2 所示。

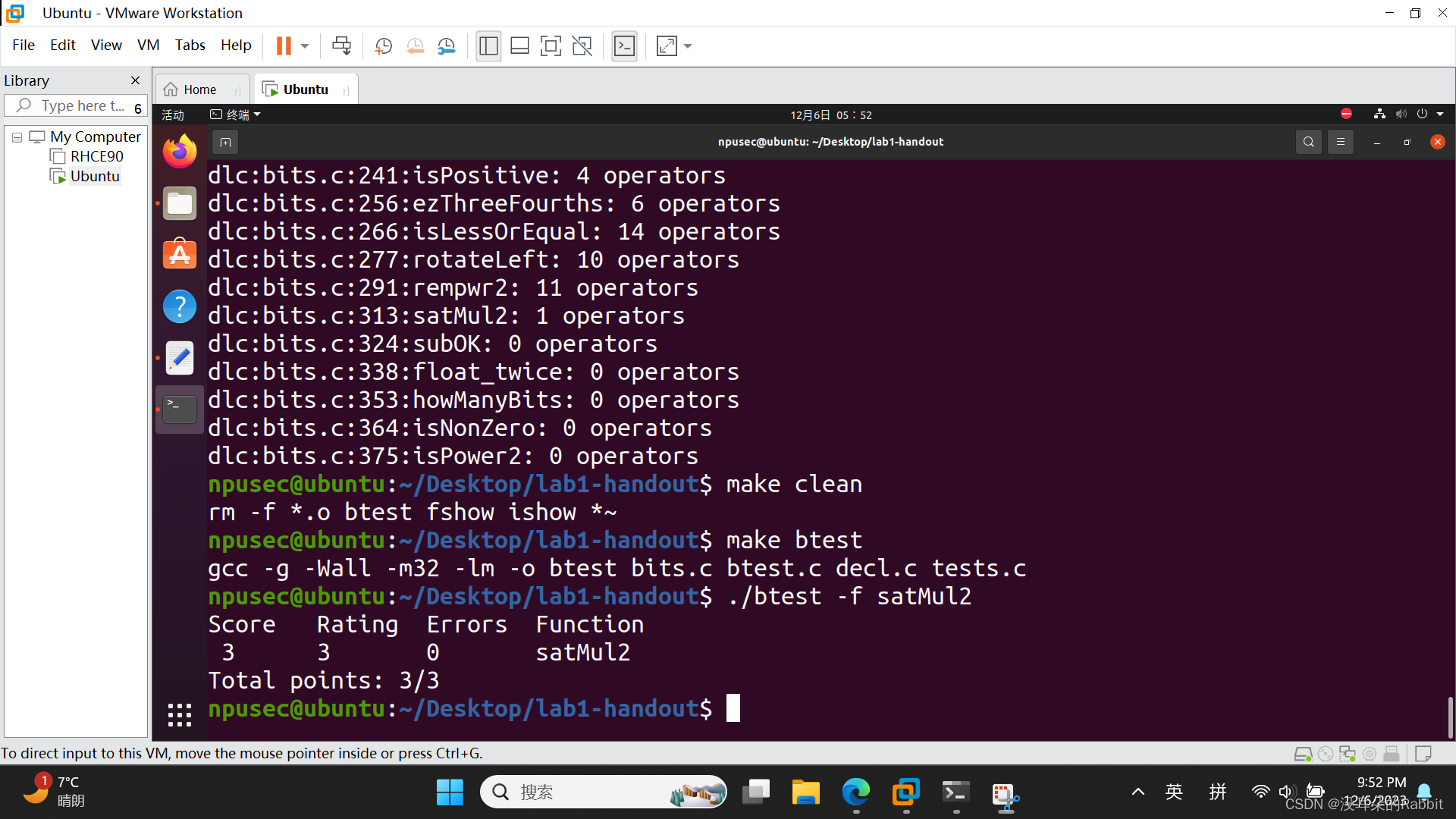
(图4:检查第12个函数satMul2)
第13个函数,subOK,如果x减去y的值能被int类型大小的变量装得下,就返回1,否则返回0。接着我们发现,当x与y同号时,不可能出现装不下也就是溢出的问题,只有当x与y异号时,才可能会用装不下也就是溢出的问题,顺着这个思路,我们可以分成两类来讨论。而分类的依据则是x^~y,当x与y同号时,x^~y的符号位为1,当x与y异号时,x^~y的符号位为0。顺着这个思路,写出下面的大框架:
(( (x^~y)&( ) | ( ~(x^~y)&( ) ) ) >>31)&1
当x与y同号时,x与~y异号,x^~y的符号位为1,此时x减去y的值一定能被int类型大小的变量装得下,所以此时返回1即可。这时大框架即为:
(( (x^~y) | ( ~(x^~y)&( ) ) ) >>31)&1
而当x与y异号时,x与~y同号,x^~y的符号位为0,此时如果x与x-y=x+~y+1异号,那么必定发生了溢出,x减去y的值一定不能被int类型大小的变量装得下,所以选择表达式~(x^(x+~y+1)),当x与x-y同号时,说明可以装得下,应该返回1,而~(x^(x+~y+1))的符号位恰好就是1;当当x与x-y异号时,说明不可以装得下,应该返回0,而~(x^(x+~y+1))的符号位恰好就是0。所以最终的大框架即为:
(( (x^~y) | ( ~(x^~y)&( ~(x^(x+~y+1)) ) ) ) >>31)&1
代码如 图5:编写第13个函数subOK 所示。检查过程如 图6:检查第13个函数subOK 所示。
int flag=x^~y;return ((flag|(~flag&(~(x^(x+~y+1)))))>>31)&1;(图5:编写第13个函数subOK)
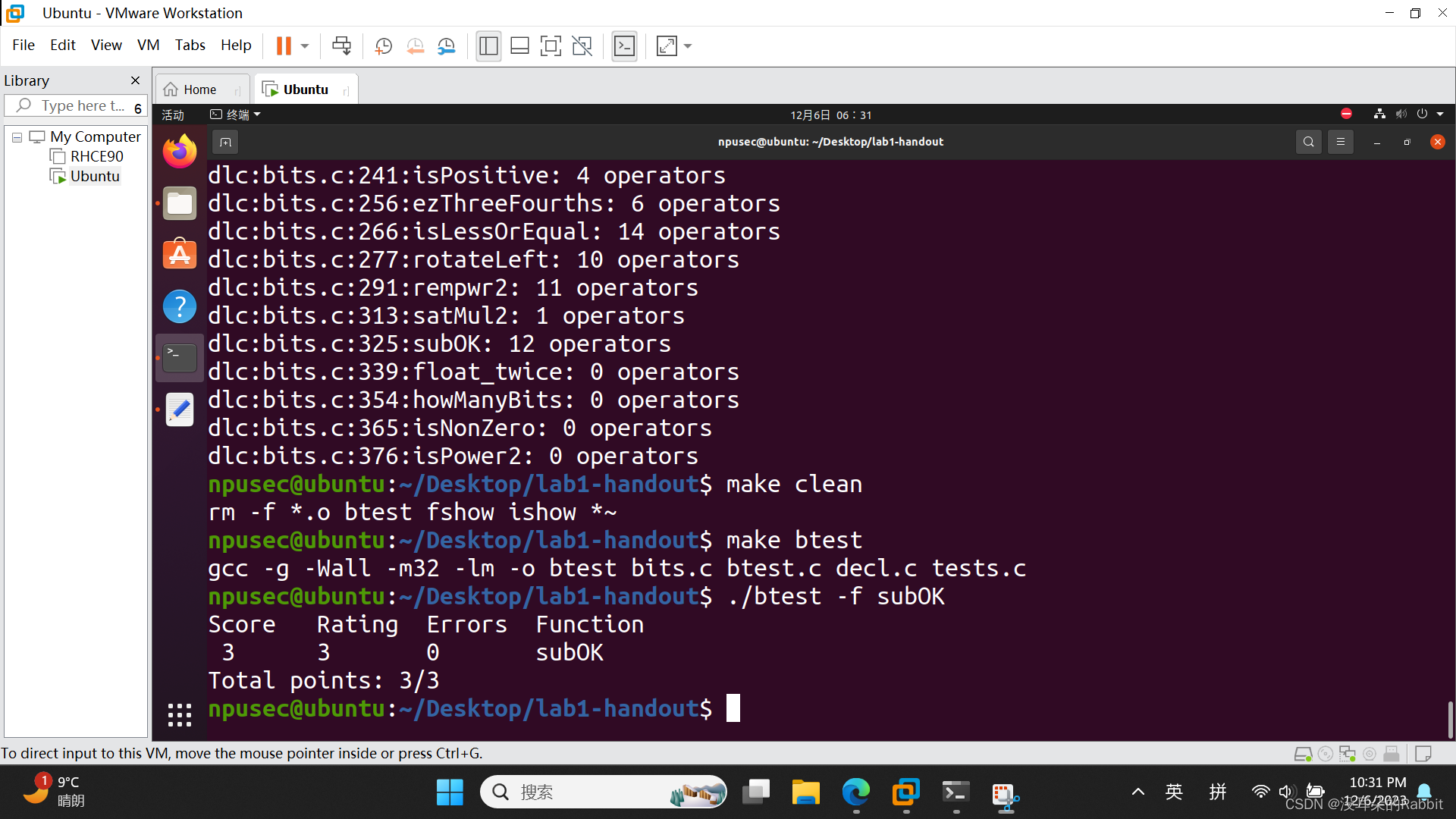
(图6:检查第13个函数subOK)
第14个函数,float_twice,在这里限制被释放,条件判断可以被使用,while语句也可以被使用,||和&&也可以被使用,而且也可以创建unsigned型的局部变量。那么这个函数要求我们做到什么呢?这个函数要求我们,对于一个浮点数f,计算2*f。举个例子来讲,如果f=0.625,那么其在计算机内部的表示形式为0x3F20 0000,计算2*f可以得到0x3FA0 0000,而这个0x3FA0 0000就是期待我们返回的值。对不起大家,在这里作者实在有点累了,所以没办法今天就讲完了。代码如 图7:编写第14个函数float_twice 所示。检查第14个函数的过程如 图8:检查第14个函数float_twice 所示
unsigned sign = 0, enow = 0, fnow = 0;unsigned pos = 1 << 31;unsigned frule = (1 << 23) - 1;if (uf == 0) {return 0;}if (uf == pos) {return uf;}sign = uf & pos;enow = (uf >> 23) & 0xff;if (enow == 0xff) {return uf;}fnow = uf & frule;if (enow == 0) {fnow = fnow << 1;if (fnow & (1 << 23)) {fnow = fnow & frule;enow += 1;}}else{enow += 1;}return sign | (enow << 23) | fnow;(图7:编写第14个函数float_twice)
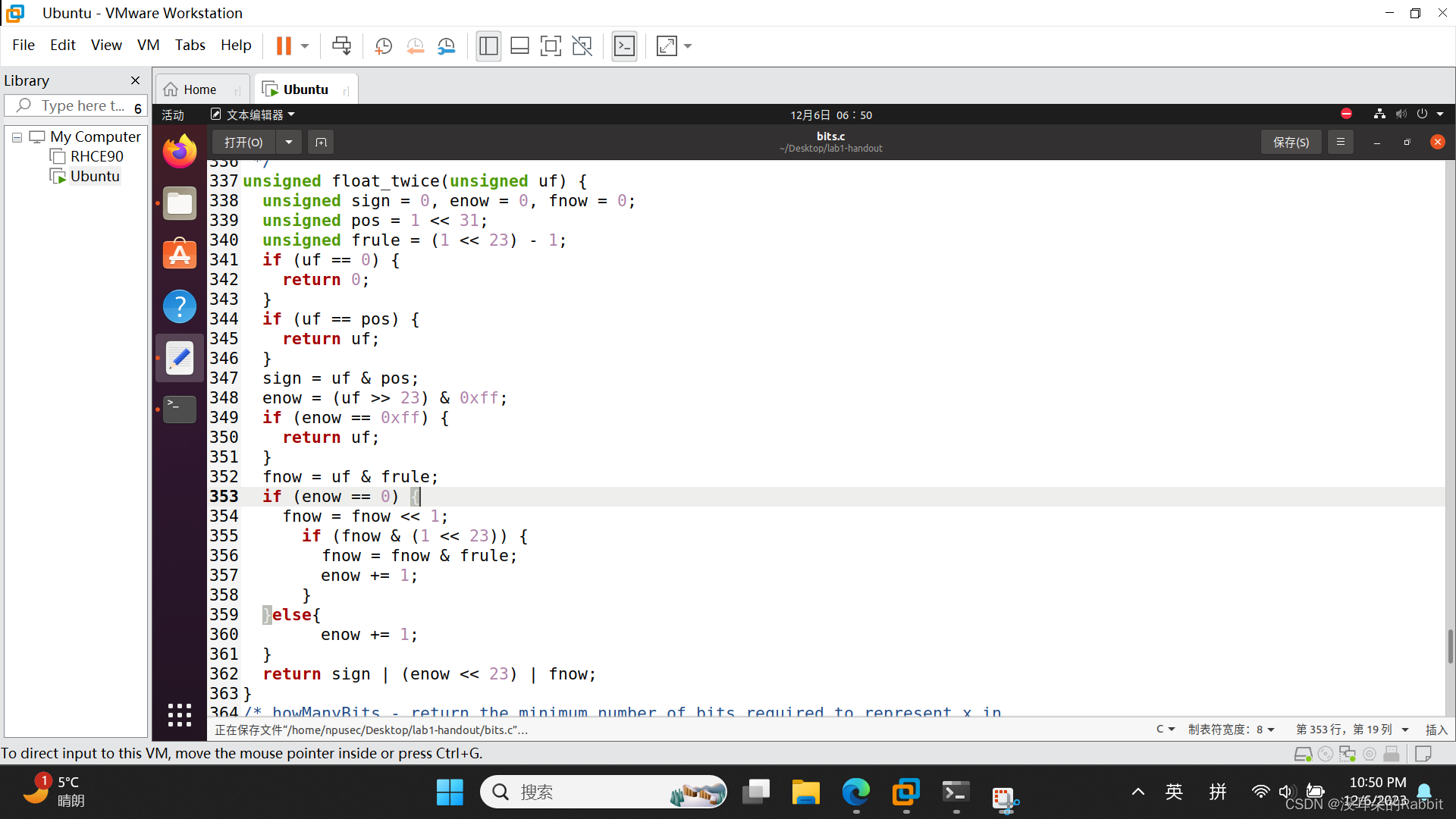
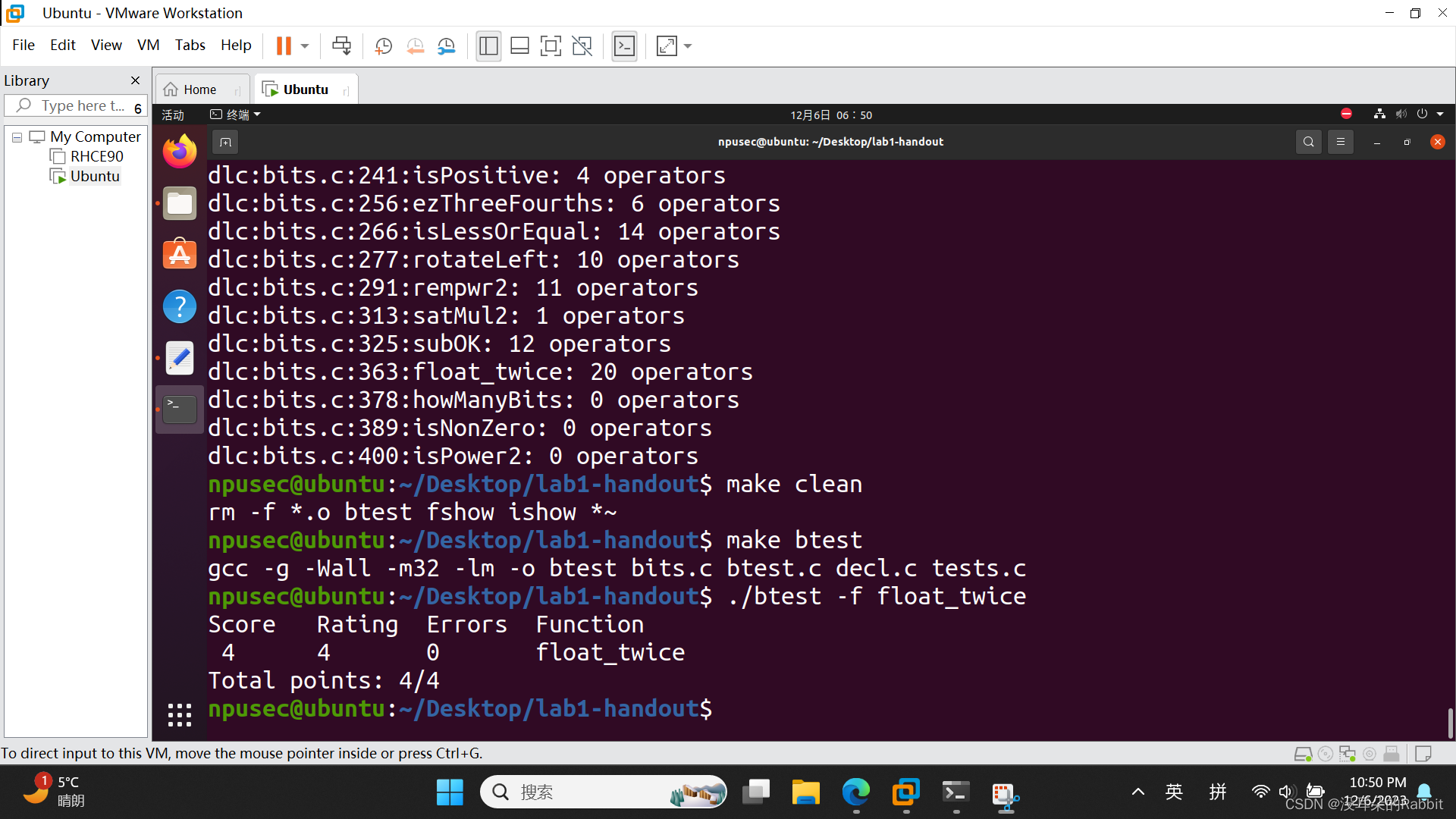
(图8:检查第14个函数float_twice)
/* * rempwr2 - Compute x%(2^n), for 0 <= n <= 30* Negative arguments should yield negative remainders* Examples: rempwr2(15,2) = 3, rempwr2(-35,3) = -3* Legal ops: ! ~ & ^ | + << >>* Max ops: 20* Rating: 3*/
int rempwr2(int x, int n) {int s = x>>31;x = (x+s)^s;x &= ((~0)+(1<<n));return (x^s)+~s+1;
}
/** satMul2 - multiplies by 2, saturating to Tmin or Tmax if overflow* Examples: satMul2(0x30000000) = 0x60000000* satMul2(0x40000000) = 0x7FFFFFFF (saturate to TMax)* satMul2(0x80034000) = 0x80000000 (saturate to TMin)* Legal ops: ! ~ & ^ | + << >>* Max ops: 20* Rating: 3*/
int satMul2(int x) {// int x2=x<<1;// int sx2=x2>>31;// int flag=(x^x2)>>31;// int tmin=1<<31;return x<<1;// return ((~flag&x2)+(flag&(~(!!x2)+1)&(sx2+tmin)));// int isx2zero=!x2;// int x2notzero=!isx2zero;// return ((~flag&x2)+(flag&(~(!!x2)+1)&(~x2notzero&(sx2+tmin))));// int istmin=!(x^tmin);// return ((istmin<<31)|((~istmin)&((~flag&x2)|(flag&(sx2+tmin)))));
}
/* * subOK - Determine if can compute x-y without overflow* Example: subOK(0x80000000,0x80000000) = 1,* subOK(0x80000000,0x70000000) = 0, * Legal ops: ! ~ & ^ | + << >>* Max ops: 20* Rating: 3*/
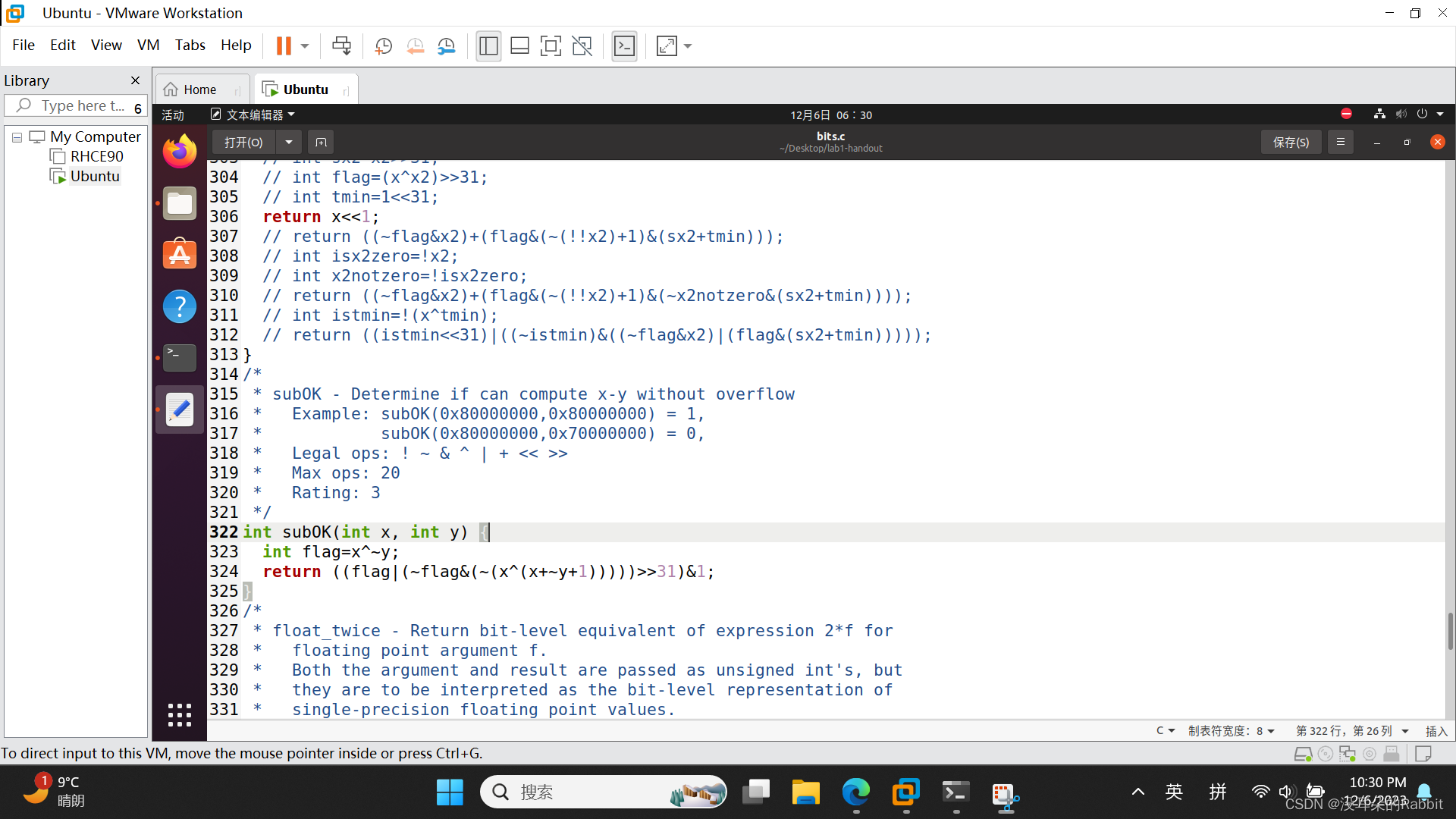
int subOK(int x, int y) {int flag=x^~y;return ((flag|(~flag&(~(x^(x+~y+1)))))>>31)&1;
}
/* * float_twice - Return bit-level equivalent of expression 2*f for* floating point argument f.* Both the argument and result are passed as unsigned int's, but* they are to be interpreted as the bit-level representation of* single-precision floating point values.* When argument is NaN, return argument* Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while* Max ops: 30* Rating: 4*/
unsigned float_twice(unsigned uf) {unsigned sign = 0, enow = 0, fnow = 0;unsigned pos = 1 << 31;unsigned frule = (1 << 23) - 1;if (uf == 0) {return 0;}if (uf == pos) {return uf;}sign = uf & pos;enow = (uf >> 23) & 0xff;if (enow == 0xff) {return uf;}fnow = uf & frule;if (enow == 0) {fnow = fnow << 1;if (fnow & (1 << 23)) {fnow = fnow & frule;enow += 1;}}else{enow += 1;}return sign | (enow << 23) | fnow;
}





)





:BM11 链表相加(二))






