有意向获取代码，请转文末观看代码获取方式~也可转原文链接获取~

1 基本定义

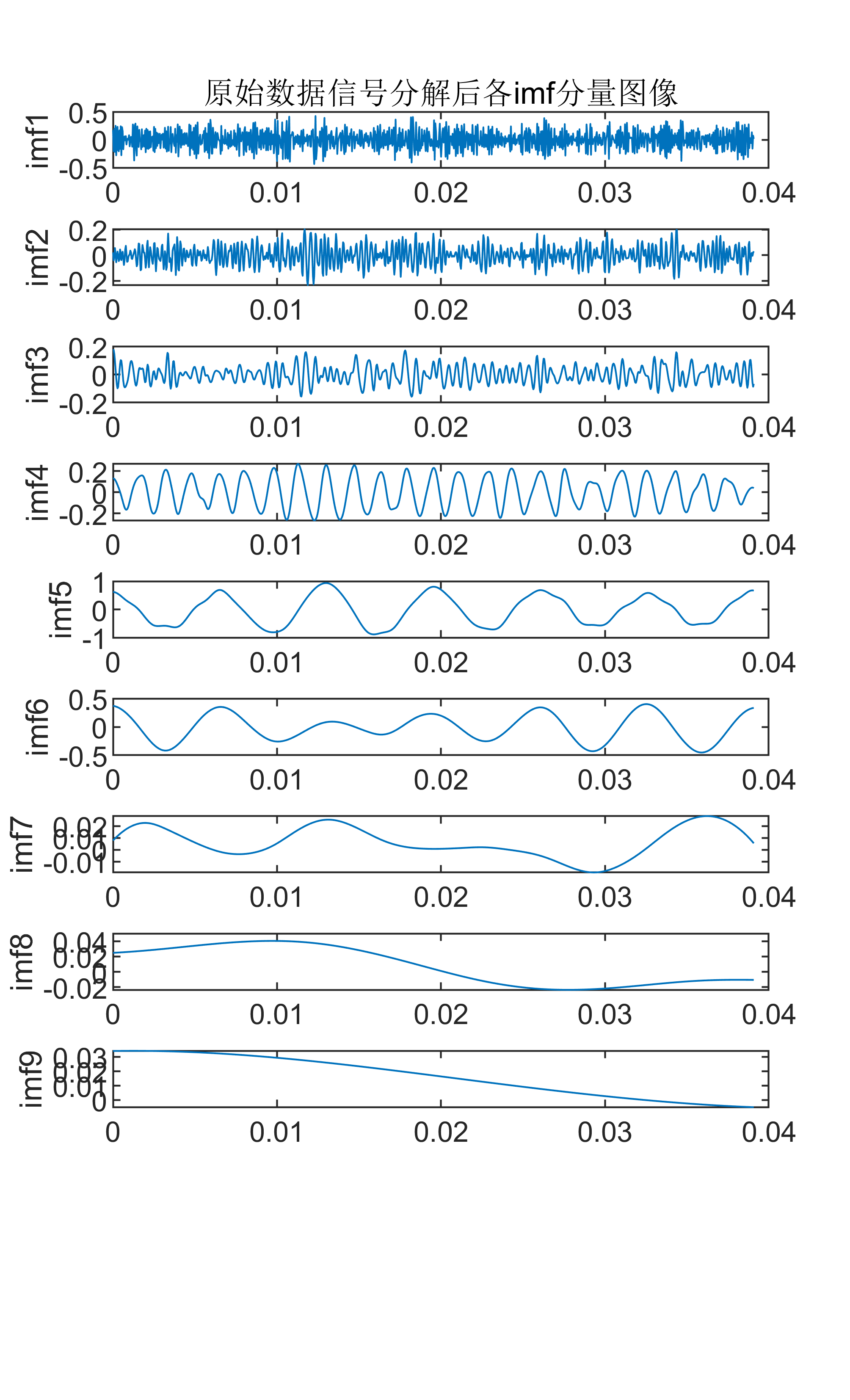
辛几何模态分解（CEEMDAN）是一种处理非线性和非平稳信号的适应性信号分解方法。通过在信号中加入白噪声，并多次进行经验模态分解（EMD），从而获得原信号的多种本征模态函数（IMF）。这些IMF可以更好地捕捉到信号中的局部特征，特别是对于非线性、非平稳信号。

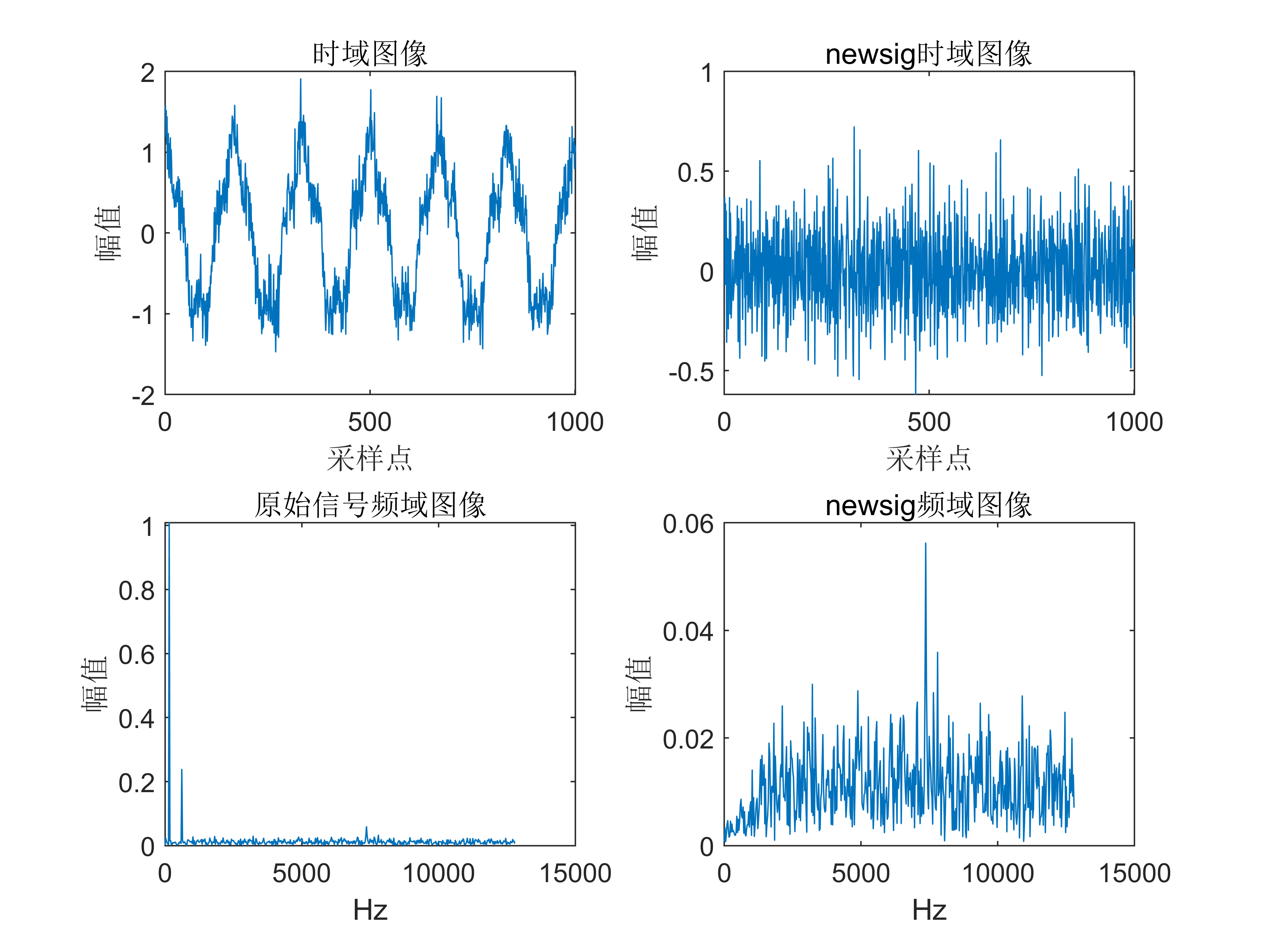
快速傅里叶变换（FFT）是一种高效的计算离散傅里叶变换（DFT）和其逆变换的算法。它可以在短时间内计算出信号在频域上的表达，从而提供信号的频率特征。

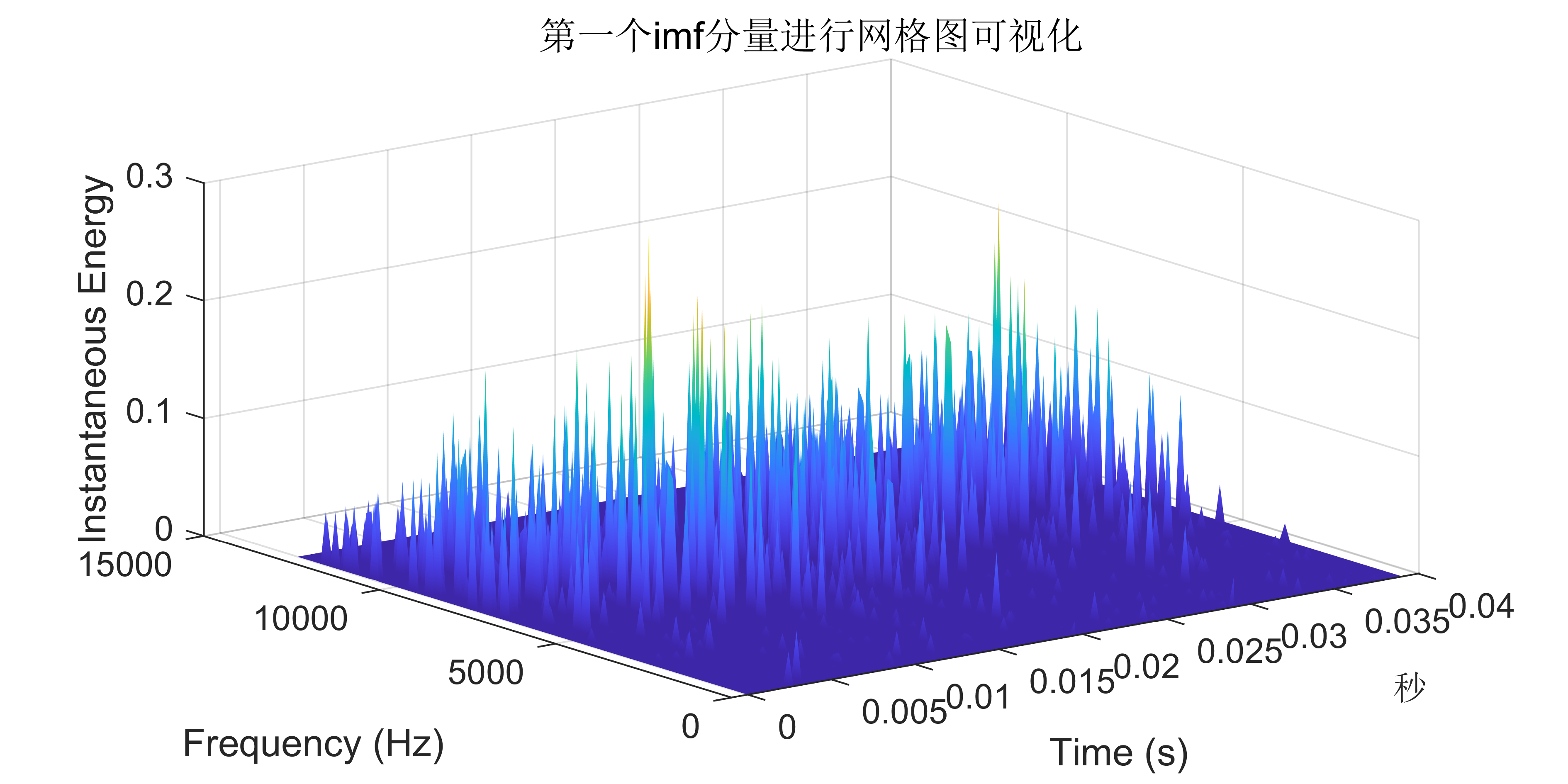
希尔伯特-黄变换（HHT）是一种用于分析非线性和非平稳信号的数学工具。它通过将信号分解成一系列固有模态函数（IMF），并计算每个IMF的瞬时频率，从而提供信号的时频特征。

将CEEMDAN、FFT和HHT组合在一起，可以形成一种强大的分析方法。首先，使用CEEMDAN将原始信号分解成多个IMF，然后对每个IMF进行FFT计算其频谱，最后使用HHT分析其时频特征。这种组合方法可以综合利用三种方法的优点，对于处理非线性和非平稳信号具有较高的准确性和鲁棒性。

此外，这种组合方法还可以用于其他领域。例如，在图像处理中，可以使用CEEMDAN将图像分解成多个区域，使用FFT计算每个区域的频谱，使用HHT分析每个区域的时频特征，从而更好地理解和分析图像的性质和行为。

总的来说，辛几何模态分解+FFT+HHT 组合算法是一种非常强大的分析方法，具有广泛的应用前景和潜力。通过充分了解和掌握这些算法的原理和应用，可以更好地解决各种实际问题，推动相关领域的发展和进步。

除了在信号处理和图像处理中的应用，这种组合方法还可以用于其他领域。例如，在机械故障诊断中，可以使用CEEMDAN将机器的振动信号分解成多个IMF，然后对每个IMF进行FFT计算其频谱，最后使用HHT分析其时频特征。这样可以准确地识别出机器的故障源，提高故障诊断的准确性和效率。

此外，这种组合方法还可以用于地球物理学、海洋学、气候学等领域。例如，在地球物理学中，可以使用CEEMDAN将地球的电磁信号分解成多个IMF，然后对每个IMF进行FFT计算其频谱，最后使用HHT分析其时频特征。这样可以更好地理解和研究地球的电磁场和地震活动。

总的来说，辛几何模态分解+FFT+HHT组合算法是一种非常通用的分析方法，可以应用于许多领域，为相关领域的发展和进步提供了强有力的支持。

此外，这种组合方法还可以用于医学图像处理和分析。例如，在医学图像中，可以使用CEEMDAN将图像分解成多个区域，使用FFT计算每个区域的频谱，使用HHT分析每个区域的时频特征，从而更好地理解和分析医学图像的性质和病变。

在生物医学工程中，这种组合方法可以应用于心电信号的处理。心电图(ECG)是一种用于监测心脏电活动的信号。使用CEEMDAN可以将ECG信号分解为多个IMF，然后使用FFT计算每个IMF的频谱，最后使用HHT分析每个IMF的时频特征。这样可以更好地理解和分析心脏电活动的特征和异常。

在环境科学领域，这种组合方法可以应用于大气污染物的监测和分析。使用CEEMDAN可以将大气污染物浓度时间序列分解为多个IMF，使用FFT计算每个IMF的频谱，最后使用HHT分析每个IMF的时频特征。这样可以更好地理解和分析大气污染物的时空分布和变化规律。

总的来说，辛几何模态分解+FFT+HHT组合算法具有广泛的应用前景和潜力，可以应用于许多领域，为相关领域的发展和进步提供了强有力的支持。

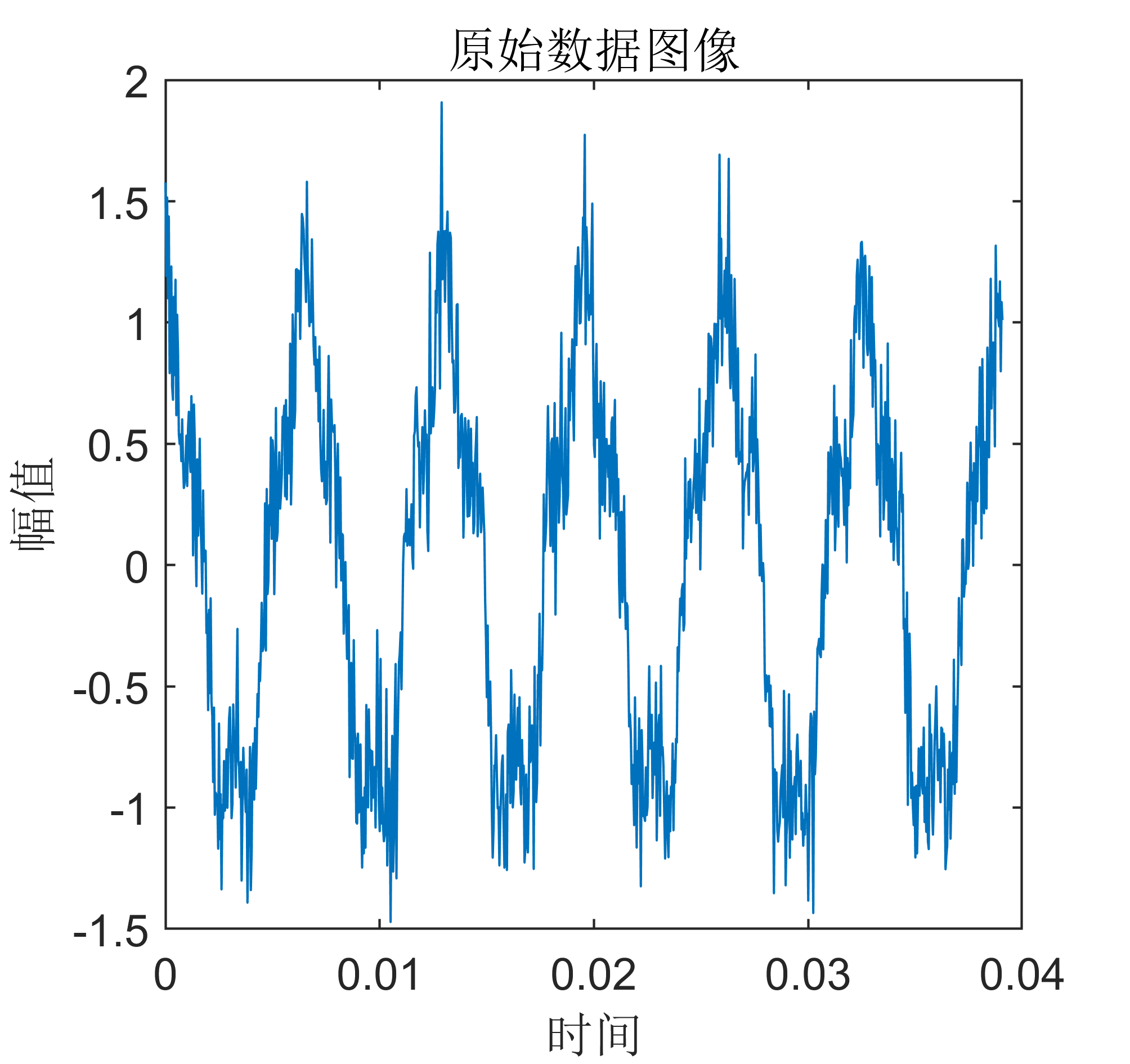
2 出图效果

附出图效果如下：

附视频教程操作：