题目
用matlab对572所在区间分别进行分段线性插值、三次样条插值,计算出151,159,984,995的对数值,画出图形并在图形上用红色圆圈标记151,159,984,995所在的点,同时在图形中显示这些点的坐标。
说明:假设125,528,765;则插值区间为【120,770】
1.分段线性插值、三次样条插值
1.1分段线性插值
Step1:根据已知 的取值点,求出每个取值点对应的线性插值多项式,表示为:
L j ( x ) = x − x j − 1 x j − x j − 1 y j − 1 + x − x j − 1 x j − x j − 1 y j L_{j}(x)=\frac{x-x_{j-1}}{x_{j}-x_{j-1}}y_{j-1}+ \frac{x-x_{j-1}}{x_{j}-x_{j-1}}y_{j} Lj(x)=xj−xj−1x−xj−1yj−1+xj−xj−1x−xj−1yj
Step2:根据已知的取值点,使用第一步中求出的每个取值点对应的线性插值多项式,然后求已知 个点对应的线性插值多项式 。其表达式为:
L ( x ) = ∑ j = 0 n y j L j ( x ) L (x)=\sum_{j=0}^{n} y_{j}L_{j}(x) L(x)=j=0∑nyjLj(x)
选取以150开始,间隔为50,到1000结束的点,然后使用分段线性插值法,计算出151,159,984,995的对数值。
x = 150:50:1000;
y = B(15:5:100)+2.*B(b==10);
figure(2)xx=[151,159,984,995];
for i=1:4yy(i)=fdxx(x,y,xx(i));
end
xx1=150:1:999;
for i=1:850yyy(i)=fdxx(x,y,xx1(i));
end
plot(xx1,yyy)
hold on
scatter(xx,yy)
text(xx,yy, {'151','159','984','995'}, 'VerticalAlignment', 'bottom', 'HorizontalAlignment', 'right'); % 添加文字标注
hold on
grid on
plot(x,y,'o')
% 添加坐标轴标签和标题
xlabel('x');
ylabel('ln(x)');
title('插值点与分段线性插值');
legend('分段线性插值点坐标','插值点')% 显示图形
grid on;
function yy=fdxx(x,y,xx)n=size(x,2);for i=1:n-1if x(i)<xx&&xx<x(i+1)L1=(xx-x(i+1))/(x(i)-x(i+1));L2=(xx-x(i))/(x(i+1)-x(i));yy=L1*y(i)+L2*y(i+1);break;elseif x(i)==xxyy=y(i); endendend
结果如下所示
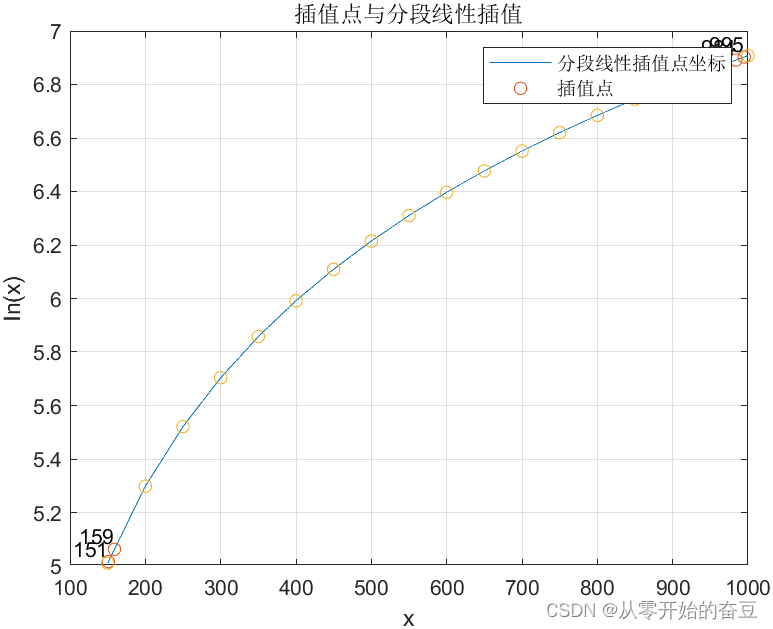
1.2三次样条插值
假设已知一组数据点的横坐标为$ x0, x1, …, xn$,纵坐标为 y 0 , y 1 , . . . , y n y0, y1, ..., yn y0,y1,...,yn。
-
计算每个小区间的一阶导数,可以使用自然边界条件或固定边界条件来确定边界处的导数值。
-
在每个小区间 [xi, xi+1] 内,拟合一个三次多项式 Si(x),使得在该区间内的插值函数满足连续性和二阶导数连续性。
三次多项式 Si(x) 的一般形式为:
S i ( x ) = a i + b i ( x − x i ) + c i ( x − x i ) 2 + d i ( x − x i ) 3 Si(x) = ai + bi(x - xi) + ci(x - xi)^2 + di(x - xi)^3 Si(x)=ai+bi(x−xi)+ci(x−xi)2+di(x−xi)3其中,$ai, bi, ci, di $是待求的系数。
-
为了确定这些系数,需要满足以下条件:
a) 在每个小区间内,插值函数与已知数据点相等:
S i ( x i ) = y i Si(xi) = yi Si(xi)=yib) 在每个小区间内,插值函数的一阶导数连续:
S i ′ ( x i + 1 ) = S i + 1 ′ ( x i + 1 ) Si'(xi+1) = Si+1'(xi+1) Si′(xi+1)=Si+1′(xi+1)c) 在每个小区间内,插值函数的二阶导数连续:
S i ′ ′ ( x i + 1 ) = S i + 1 ′ ′ ( x i + 1 ) Si''(xi+1) = Si+1''(xi+1) Si′′(xi+1)=Si+1′′(xi+1) -
使用这些条件,可以得到一个三对角线性方程组,通过求解该方程组即可得到每个小区间的系数。
方程组的形式为:
h i ∗ c i − 1 + 2 ( h i + h i + 1 ) ∗ c i + h i + 1 ∗ c i + 1 = 3 ∗ ( ( y i + 1 − y i ) / h i + 1 − ( y i − y i − 1 ) / h i ) h_i * ci-1 + 2(h_i + h_i+1) * ci + h_i+1 * ci+1 = 3 * ((y_i+1 - y_i) / h_i+1 - (y_i - y_i-1) / h_i) hi∗ci−1+2(hi+hi+1)∗ci+hi+1∗ci+1=3∗((yi+1−yi)/hi+1−(yi−yi−1)/hi)其中,$h_i = x_i+1 - x_i $是每个小区间的宽度。
-
求解得到系数后,即可得到每个小区间的三次多项式 Si(x)。
-
最后,根据所需的插值点 x,找到对应的小区间 [xi, xi+1],然后使用对应的三次多项式 Si(x) 计算插值点的函数值。
1.3 代码实现
%%三次样条插值
figure(3)
s=threesimple1(x,y,xx1);
plot(xx1,s)
hold on
grid on
plot(x,y,'o')
yy=threesimple1(x,y,xx);
scatter(xx,yy)
text(xx,yy, {'151','159','984','995'}, 'VerticalAlignment', 'bottom', 'HorizontalAlignment', 'right'); % 添加文字标注xlabel('x'), ylabel('ln(x)')
title('插值点与三次样条函数')
legend('三次样条插值点坐标','插值点')
function [D,h,A,g,M]=threesimple(X,Y)
% 自然边界条件的三次样条函数(第二种边界条件)
% 此函数为M值求值函数
% D,h,A,g,M输出量分别为系数矩阵D,插值宽度h,差商表A,g值,M值 n=length(X); A=zeros(n,n);A(:,1)=Y';D=zeros(n-2,n-2);g=zeros(n-2,1);for j=2:nfor i=j:nA(i,j)=(A(i,j-1)- A(i-1,j-1))/(X(i)-X(i-j+1));endendfor i=1:n-1h(i)=X(i+1)-X(i);endfor i=1:n-2D(i,i)=2;g(i,1)=(6/(h(i+1)+h(i)))*(A(i+2,2)-A(i+1,2));endfor i=2:n-2u(i)=h(i)/(h(i)+h(i+1));n(i-1)=h(i)/(h(i-1)+h(i));D(i-1,i)=n(i-1);D(i,i-1)=u(i); endM=D\g;M=[0;M;0];
endfunction s=threesimple1(X,Y,x)
% 自然边界条件函数
% s函数表示三次样条插值函数插值点对应的函数值
% 根据三次样条参数函数求出的D,h,A,g,M
% x表示求解插值点函数点,X为已知插值点 [D,h,A,g,M]=threesimple(X,Y)n=length(X); m=length(x); for t=1:mfor i=1:n-1if (x(t)<=X(i+1))&&(x(t)>=X(i))p1=M(i,1)*(X(i+1)-x(t))^3/(6*h(i));p2=M(i+1,1)*(x(t)-X(i))^3/(6*h(i));p3=(A(i,1)-M(i,1)/6*(h(i))^2)*(X(i+1)-x(t))/h(i);p4=(A(i+1,1)-M(i+1,1)/6*(h(i))^2)*(x(t)-X(i))/h(i);s(t)=p1+p2+p3+p4; break;elses(t)=0; endendend
end结果如下所示:
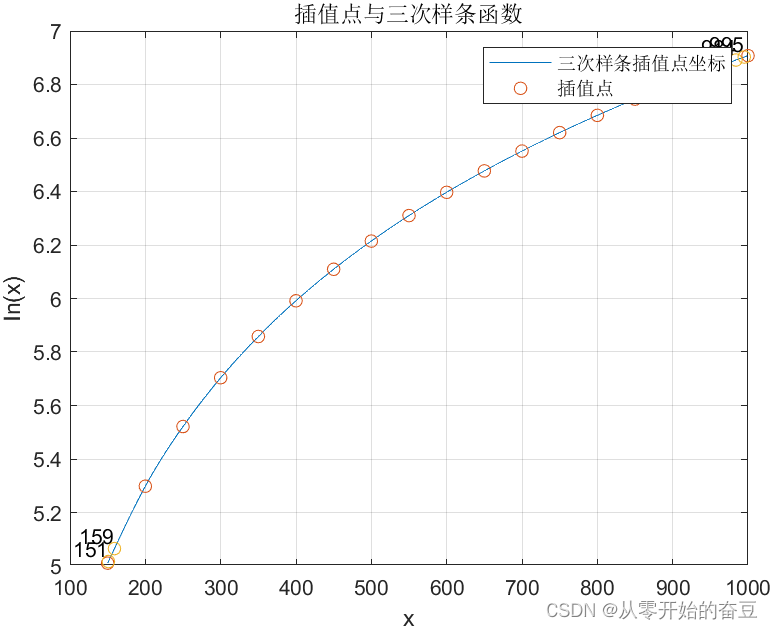



(第一期))

)




)
:HuggingGPT根据用户需求自动调用Huggingface合适的模型)

-- Linux 基本安全防护技术)
【STL的概念,STL的历史缘由,STL六大组件、STL的重要性、以及如何学习STL、STL的缺陷的讲解】)




