文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:二叉树的完全性检验
出处:958. 二叉树的完全性检验
难度
5 级
题目描述
要求
给定一个二叉树的根结点 root \texttt{root} root,确定它是否是一个完全二叉树。
在一个完全二叉树中,除了最后一层以外,每一层都是完全填满的,并且最后一层的所有结点都是尽可能靠左的。如果最后一层是第 h \texttt{h} h 层,则可以包含 1 \texttt{1} 1 到 2 h \texttt{2}^\texttt{h} 2h 个结点。
示例
示例 1:
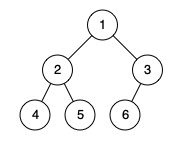
输入: root = [1,2,3,4,5,6] \texttt{root = [1,2,3,4,5,6]} root = [1,2,3,4,5,6]
输出: true \texttt{true} true
解释:除了最后一层以外的每一层都是满的(即,结点值为 {1} \texttt{\{1\}} {1} 和 {2, 3} \texttt{\{2, 3\}} {2, 3} 的两层),且最后一层中的所有结点( {4, 5, 6} \texttt{\{4, 5, 6\}} {4, 5, 6})都尽可能地靠左。
示例 2:
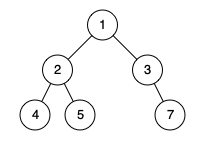
输入: root = [1,2,3,4,5,null,7] \texttt{root = [1,2,3,4,5,null,7]} root = [1,2,3,4,5,null,7]
输出: false \texttt{false} false
解释:值为 7 \texttt{7} 7 的结点没有尽可能靠左。
数据范围
- 树中结点数目在范围 [1, 100] \texttt{[1, 100]} [1, 100] 内
- 1 ≤ Node.val ≤ 1000 \texttt{1} \le \texttt{Node.val} \le \texttt{1000} 1≤Node.val≤1000
解法
思路和算法
将根结点所在层定义为第 0 0 0 层。如果完全二叉树有 l l l 层,则当 i < l − 1 i < l - 1 i<l−1 时,完全二叉树的第 i i i 层有 2 i 2^i 2i 个结点,当 i = l − 1 i = l - 1 i=l−1 时,完全二叉树的第 i i i 层的结点数在范围 [ 1 , 2 i ] [1, 2^i] [1,2i] 内且所有结点都尽可能靠左。
为了判断给定的二叉树是否是完全二叉树,可以假设给定的二叉树是完全二叉树,判断是否符合完全二叉树的性质。
由于完全二叉树要求每一层结点都符合完全二叉树的性质,因此可以使用层序遍历判断给定的二叉树是否是完全二叉树。
从根结点开始依次遍历每一层的结点,在层序遍历的过程中需要区分不同结点所在的层,确保每一轮访问的结点为同一层的全部结点。遍历每一层结点之前首先得到当前层的结点数,即可确保每一轮访问的结点为同一层的全部结点。遍历每一层的同时需要维护每一层填满时的结点数,根结点所在层的结点数是 1 1 1,当一层结点遍历结束之后,下一层填满时的结点数为当前层填满时的结点数的两倍。以下将一层填满时的结点数称为该层的满结点数,则第 i i i 层的满结点数是 2 i 2^i 2i。
遍历每一层结点之前首先得到当前层的结点数,判断当前层是否为最后一层。如果当前层的实际结点数等于当前层的满结点数,则当前层不一定是最后一层;如果当前层的实际结点数小于当前层的满结点数,则当前层一定是最后一层。对于两种情况,判断是否符合完全二叉树性质的做法分别如下。
-
如果当前层不一定是最后一层,则判断当前层的子结点是否符合完全二叉树的性质。从左到右依次遍历当前层的结点,对于当前层的每个结点依次判断左子结点和右子结点是否为空。如果在一个空子结点之后遇到一个非空子结点,则子结点不符合所有的结点尽可能靠左,因此子结点不符合完全二叉树的性质,返回 false \text{false} false。
-
如果当前层一定是最后一层,则判断当前层的结点是否符合完全二叉树的性质。当前层的每个结点都必须是叶结点,不能有非空子结点。如果当前层至少有一个结点有非空子结点,则不符合完全二叉树的性质,返回 false \text{false} false。
如果遍历结束之后没有发现不符合完全二叉树性质的情况,则给定的二叉树是完全二叉树,返回 true \text{true} true。
由于在遍历填满结点的每一层时,都会判断下一层结点是否符合完全二叉树的性质,当下一层结点不符合所有的结点尽可能靠左时就提前返回不是完全二叉树,因此在遍历到每一层时,当前层的结点一定符合完全二叉树的性质,只需要根据当前层的实际结点数和当前层的子结点判断是否符合完全二叉树的性质,因此上述做法可以确保结果正确。
代码
class Solution {public boolean isCompleteTree(TreeNode root) {int completeSize = 1;Queue<TreeNode> queue = new ArrayDeque<TreeNode>();queue.offer(root);while (!queue.isEmpty()) {int size = queue.size();if (size == completeSize) {boolean isComplete = true;for (int i = 0; i < size; i++) {TreeNode node = queue.poll();TreeNode[] children = {node.left, node.right};for (TreeNode child : children) {if (child == null) {isComplete = false;} else {if (!isComplete) {return false;}queue.offer(child);}}}} else {for (int i = 0; i < size; i++) {TreeNode node = queue.poll();if (node.left != null || node.right != null) {return false;}}}completeSize *= 2;}return true;}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。每个结点都被访问一次。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是队列空间,队列内元素个数不超过 n n n。
)














)



