1.简述
abs函数的功能是绝对值和复数的模
语法
Y = abs(X)
说明
Y = abs(X) 返回数组 X 中每个元素的绝对值。如果 X 是复数,则 abs(X) 返回复数的模。
示例
标量的绝对值
y = abs(-5)
y = 5
向量的绝对值
创建实值的数值向量。
x = [1.3 -3.56 8.23 -5 -0.01]'
x = 5×1
1.3000
-3.5600
8.2300
-5.0000
-0.0100
计算向量元素的绝对值。
y = abs(x)
y = 5×1
1.3000
3.5600
8.2300
5.0000
0.0100
复数的模
y = abs(3+4i)
y = 5
输入数组,指定为标量、向量、矩阵或多维数组。如果 X 是复数,则它必须为 single 或 double 数组。输出数组的大小和数据类型与输入数组相同。
绝对值
实数的绝对值(或模数)是不考虑符号的非负对应值。
对于实值a,绝对值为:
如果 a 大于或等于零,则为 a
如果 a 小于零,则为 -a
abs(-0) 返回 0。
复数的模
复数的模(或模数)是在复平面中绘制的向量(从原点到复数值)的长度。
2.代码
主程序:
function f = f1220(x)
%输入各个点的坐标值,及目标函数值
a=[1 4 3 5 9 12 6 20 17 8];
b=[2 10 8 18 1 4 5 10 8 9];
f(1) = abs(x(1)-a(1))+abs(x(2)-b(1));
f(2) = abs(x(1)-a(2))+abs(x(2)-b(2));
f(3) = abs(x(1)-a(3))+abs(x(2)-b(3));
f(4) = abs(x(1)-a(4))+abs(x(2)-b(4));
f(5) = abs(x(1)-a(5))+abs(x(2)-b(5));
f(6) = abs(x(1)-a(6))+abs(x(2)-b(6));
f(7) = abs(x(1)-a(7))+abs(x(2)-b(7));
f(8) = abs(x(1)-a(8))+abs(x(2)-b(8));
f(9) = abs(x(1)-a(9))+abs(x(2)-b(9));
f(10) = abs(x(1)-a(10))+abs(x(2)-b(10));
子程序:
%ABS Absolute value.
% ABS(X) is the absolute value of the elements of X. When
% X is complex, ABS(X) is the complex modulus (magnitude) of
% the elements of X.
%
% See also SIGN, ANGLE, UNWRAP, HYPOT.
% Copyright 1984-2005 The MathWorks, Inc.
% Built-in function.
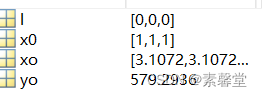
3.运行结果







![[驱动开发]gpio子系统及中断实现led亮灭](http://pic.xiahunao.cn/[驱动开发]gpio子系统及中断实现led亮灭)





)


:从零开始实现线性回归的训练)


