文章目录
- 例题——239. 滑动窗口最大值
- 相关练习
- 1438. 绝对差不超过限制的最长连续子数组
- 解法1——两个单调队列分别维护最大值和最小值
- 解法2——有序集合TreeMap
- 2398. 预算内的最多机器人数目
- 解法1——二分答案 + 单调队列
- 解法2——双指针 + 单调队列 (不固定大小的滑动窗口)⭐
- 思考——把「子数组」改成「子序列」要怎么做?1383. 最大的团队表现值🐂
- 解法——排序+利用堆
- 862. 和至少为 K 的最短子数组⭐⭐⭐⭐⭐
- 解法1——单调队列
- 1499. 满足不等式的最大值
- 解法——单调队列
https://www.bilibili.com/video/BV1bM411X72E/
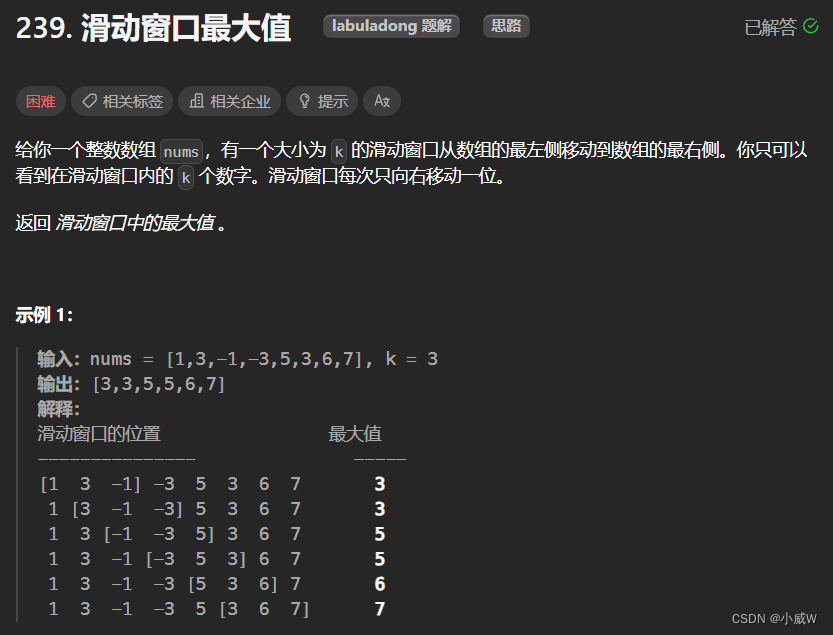
例题——239. 滑动窗口最大值
https://leetcode.cn/problems/sliding-window-maximum/description/
提示:
1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
1 <= k <= nums.length
模板题,维护一个固定长度窗口内的最大值。
单调队列是递减的,这样队首的就i是窗口中的最大值。
class Solution {public int[] maxSlidingWindow(int[] nums, int k) {Deque<Integer> dq = new ArrayDeque<>();int n = nums.length;int[] ans = new int[n - k + 1];for (int i = 0; i < n; ++i) {// 维护单调队列的单调性while (!dq.isEmpty() && nums[i] > nums[dq.peekLast()]) dq.pollLast();// 移除窗口外的元素while (!dq.isEmpty() && dq.peekFirst() <= i - k) dq.pollFirst();dq.offerLast(i); // 加入单调队列if (i >= k - 1) ans[i - k + 1] = nums[dq.peekFirst()];}return ans;}
}
相关练习
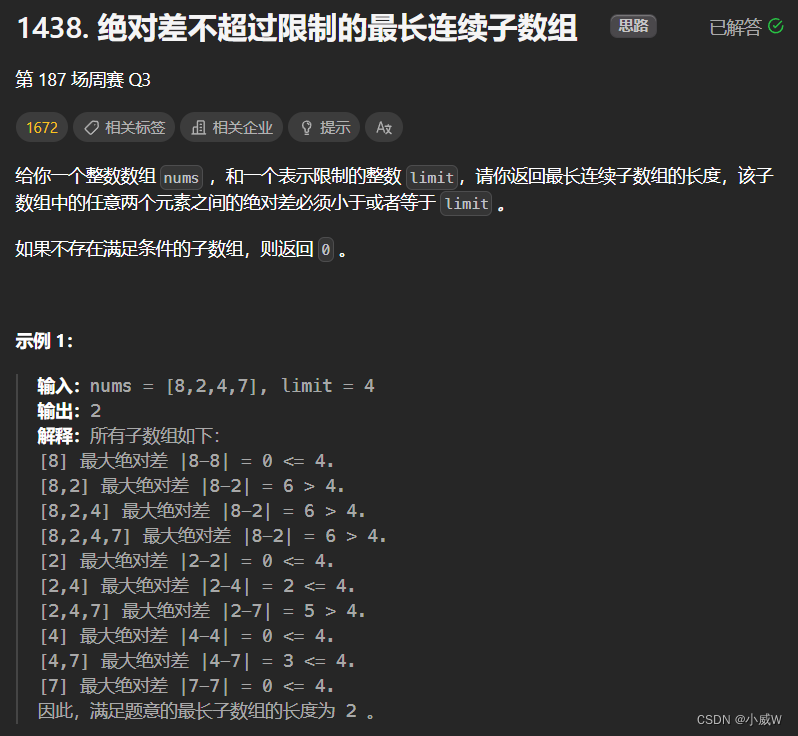
1438. 绝对差不超过限制的最长连续子数组
https://leetcode.cn/problems/longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit/description/
提示:
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^9
0 <= limit <= 10^9
解法1——两个单调队列分别维护最大值和最小值
使用两个单调队列分别维护窗口中的最大值和最小值,当最大值和最小值之间的差不符合条件时,将两个队列中靠左的位置移除直到满足条件。
class Solution {public int longestSubarray(int[] nums, int limit) {int ans = 0, n = nums.length, st = 0;Deque<Integer> dq1 = new ArrayDeque<>(), dq2 = new ArrayDeque<>();for (int i = 0; i < n; ++i) {while (!dq1.isEmpty() && nums[i] >= nums[dq1.peekLast()]) dq1.pollLast();while (!dq2.isEmpty() && nums[i] <= nums[dq2.peekLast()]) dq2.pollLast();dq1.offer(i);dq2.offer(i);while (nums[dq1.peekFirst()] - nums[dq2.peekFirst()] > limit) {if (dq1.peekFirst() < dq2.peekFirst()) st = dq1.pollFirst() + 1;else st = dq2.pollFirst() + 1;}ans = Math.max(ans, i - st + 1);}return ans;}
}
解法2——有序集合TreeMap
class Solution {public int longestSubarray(int[] nums, int limit) {TreeMap<Integer, Integer> tm = new TreeMap<>();int ans = 0;for (int l = 0, r = 0; r < nums.length; ++r) {tm.merge(nums[r], 1, Integer::sum);while (tm.lastKey() - tm.firstKey() > limit) {tm.merge(nums[l], -1, Integer::sum);if (tm.get(nums[l]) == 0) tm.remove(nums[l]);l++;}ans = Math.max(r - l + 1, ans);}return ans;}
}
2398. 预算内的最多机器人数目
https://leetcode.cn/problems/maximum-number-of-robots-within-budget/description/

提示:
chargeTimes.length == runningCosts.length == n
1 <= n <= 5 * 10^4
1 <= chargeTimes[i], runningCosts[i] <= 10^5
1 <= budget <= 10^15
解法1——二分答案 + 单调队列
二分 k,每个子问题都类似 滑动窗口最大值。
class Solution {int[] chargeTimes, runningCosts;long budget;public int maximumRobots(int[] chargeTimes, int[] runningCosts, long budget) {this.chargeTimes = chargeTimes;this.runningCosts = runningCosts;this.budget = budget;int n = chargeTimes.length;// 二分答案int l = 0, r = n;while (l < r) {int mid = l + r + 1 >> 1;if (check(mid)) l = mid;else r = mid - 1;}return l;}public boolean check(int k) {long s = 0;// 单调递减的单调队列Deque<Integer> dq = new ArrayDeque<>();for (int i = 0; i < chargeTimes.length; ++i) {s += runningCosts[i];if (i >= k) s -= runningCosts[i - k];while (!dq.isEmpty() && chargeTimes[i] >= chargeTimes[dq.peekLast()]) {dq.pollLast();}dq.offer(i);while (!dq.isEmpty() && i - dq.peekFirst() >= k) dq.pollFirst();if (i >= k - 1 && budget >= k * s + chargeTimes[dq.peekFirst()]) return true;}return false;}
}
解法2——双指针 + 单调队列 (不固定大小的滑动窗口)⭐
class Solution {public int maximumRobots(int[] chargeTimes, int[] runningCosts, long budget) {int n = chargeTimes.length, ans = 0;long s = 0L;Deque<Integer> dq = new ArrayDeque<>();for (int l = 0, r = 0; r < n; ++r) {while (!dq.isEmpty() && chargeTimes[r] >= chargeTimes[dq.peekLast()]) dq.pollLast();dq.offerLast(r);s += runningCosts[r];// 如果左端点 left 不满足要求,就不断右移 leftwhile (!dq.isEmpty() && chargeTimes[dq.peekFirst()] + (r - l + 1) * s > budget) {if (dq.peekFirst() == l) dq.pollFirst();s -= runningCosts[l++];}ans = Math.max(ans, r - l + 1);}return ans;}
}
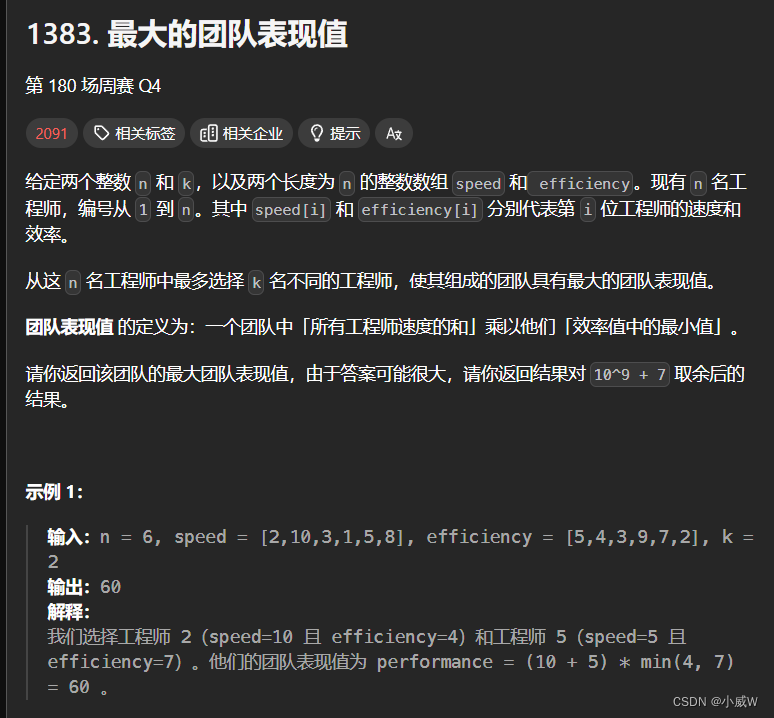
思考——把「子数组」改成「子序列」要怎么做?1383. 最大的团队表现值🐂
https://leetcode.cn/problems/maximum-performance-of-a-team/description/
提示:
1 <= k <= n <= 10^5
speed.length == n
efficiency.length == n
1 <= speed[i] <= 10^5
1 <= efficiency[i] <= 10^8
解法——排序+利用堆
根据 efficiency 从大到小排序,前面的都是可用的。
最多选择 k 个人员,则堆的大小设置为 k,每次满了去除最小的。
注意!当前最为 effciency 最小值的人员是必选的。
class Solution {public int maxPerformance(int n, int[] speed, int[] efficiency, int k) {final long MOD = (int)1e9 + 7;PriorityQueue<Integer> pq = new PriorityQueue<>();Integer[] idx = new Integer[n];Arrays.setAll(idx, e -> e);// 按效率倒序排序Arrays.sort(idx, (x, y) -> (efficiency[y] - efficiency[x]));long ans = 0, s = 0;for (int i = 0; i < n; ++i) {pq.offer(speed[idx[i]]);s += speed[idx[i]];ans = Math.max(ans, s * efficiency[idx[i]]);if (pq.size() == k) {s -= pq.poll();}}return (int)(ans % MOD);}
}
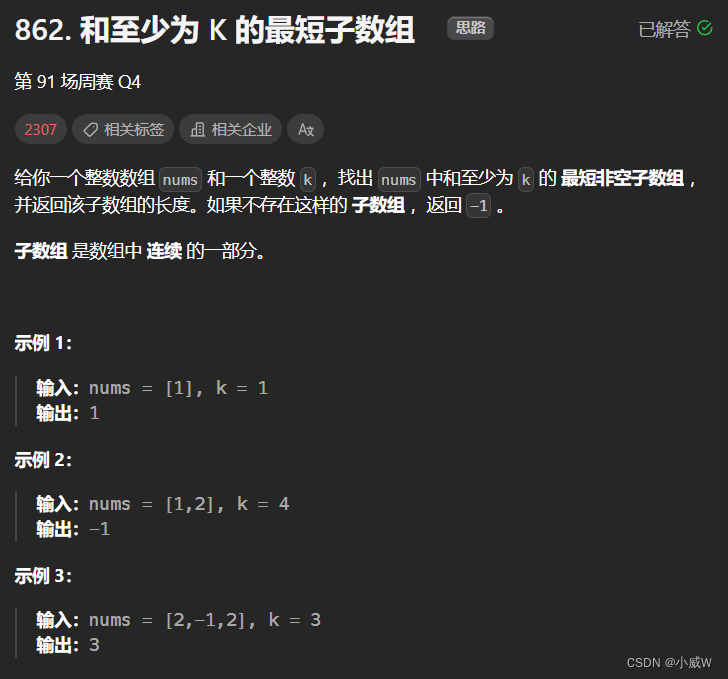
862. 和至少为 K 的最短子数组⭐⭐⭐⭐⭐
https://leetcode.cn/problems/shortest-subarray-with-sum-at-least-k/description/
提示:
1 <= nums.length <= 10^5
-10^5 <= nums[i] <= 10^5
1 <= k <= 10^9
解法1——单调队列
https://leetcode.cn/problems/shortest-subarray-with-sum-at-least-k/solutions/1925036/liang-zhang-tu-miao-dong-dan-diao-dui-li-9fvh/

class Solution {public int shortestSubarray(int[] nums, int k) {int n = nums.length, ans = n + 1;long[] s = new long[n + 1];for (int i = 0; i < n; ++i) s[i + 1] = s[i] + nums[i];// 单调递增的单调队列Deque<Integer> dq = new ArrayDeque<>();for (int i = 0; i <= n; ++i) {long curS = s[i];while (!dq.isEmpty() && curS - s[dq.peekFirst()] >= k) {ans = Math.min(ans, i - dq.pollFirst());}while (!dq.isEmpty() && s[dq.peekLast()] >= curS) {dq.pollLast();}dq.offerLast(i);}return ans == n + 1? -1: ans;}
}
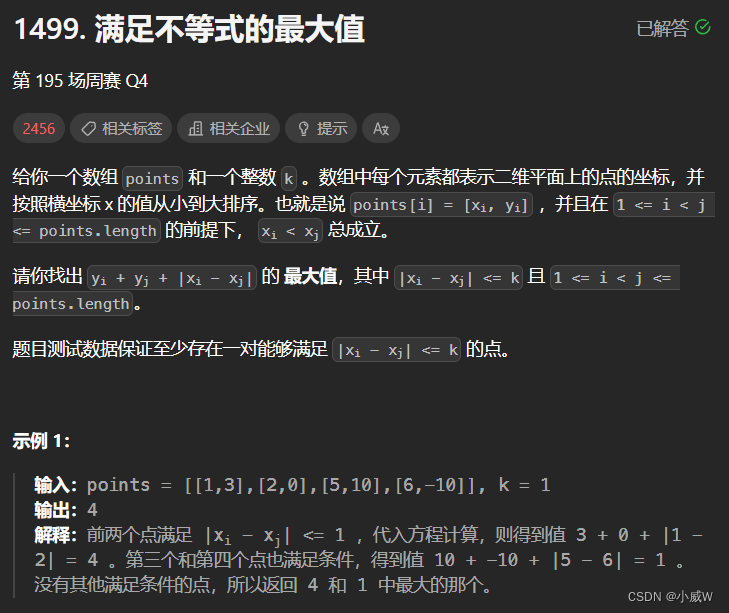
1499. 满足不等式的最大值
https://leetcode.cn/problems/max-value-of-equation/
提示:
2 <= points.length <= 10^5
points[i].length == 2
-10^8 <= points[i][0], points[i][1] <= 10^8
0 <= k <= 2 * 10^8
对于所有的1 <= i < j <= points.length ,points[i][0] < points[j][0] 都成立。也就是说,xi 是严格递增的。
解法——单调队列
按 y - x 单调递减,这样每次取最前面的计算即可。
当 x 距离较远时,需要移除位于队首的元素。
class Solution {public int findMaxValueOfEquation(int[][] points, int k) {int n = points.length, ans = Integer.MIN_VALUE;// yi+yj+xi-xj最大,即yj-xj最大,且满足xi-xj<=k// 按y-x单调递减的单调队列Deque<Integer> dq = new ArrayDeque<>();for (int i = 0; i < n; ++i) {int x = points[i][0], y = points[i][1];// 把前面不能用的去掉while (!dq.isEmpty() && x > points[dq.peekFirst()][0] + k) dq.pollFirst();if (!dq.isEmpty()) {ans = Math.max(ans, x + y + points[dq.peekFirst()][1] - points[dq.peekFirst()][0]);}// 保持单调性while (!dq.isEmpty() && y - x >= points[dq.peekLast()][1] - points[dq.peekLast()][0]) dq.pollLast();dq.offerLast(i);}return ans;}
}
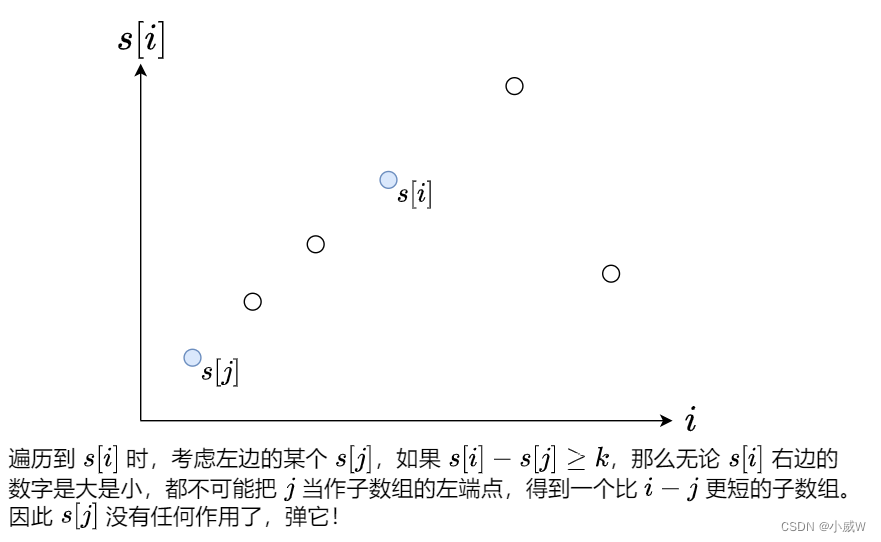
这道题目的特点是——远了的不行,要移出去。这就是出了窗口。
用单调队列 维护可以在窗口中的最大值,就可以方便地计算了。






)


通过OF函数获取属性)
)



(类的定义,访问限定符,类的作用域,类的实例化,类的对象大小,this指针))
⭐)


 - react-redux的基本使用)
![[C/C++]数据结构 关于二叉树的OJ题(利用分治思想解决难题)](http://pic.xiahunao.cn/[C/C++]数据结构 关于二叉树的OJ题(利用分治思想解决难题))