MFC 实现数字图像处理中的图像增强操作

本文使用visual Studio MFC 平台实现图像增强中典型的三种图像增强的方法中的两大类，包括线性变换–>负变换，非线性变换–>对数变换和幂律变换；其中第三大类分段式变换可以参考MFC实现图像增强–分段式变换（灰度级切片，对比度拉伸，Bit-plane slicing）
关于基础工程的创建请参考
01-Visual Studio 使用MFC 单文档工程绘制单一颜色直线和绘制渐变颜色的直线

02-visual Studio MFC 绘制单一颜色三角形、渐变颜色边框三角形、渐变填充三角形、边框渐变的正方形与填充渐变的正方形实例
03-visual Studio MFC 平台实现对灰度图添加椒盐噪声，并进行均值滤波与中值滤波

一、线性（负变换和单位变换）

线性变换的原理

图像增强中的线性变换是一种基本的像素值变换方法，通常涉及负变换和单位变换。

1. 负变换： 负变换是通过反转图像的灰度级别，使得原来的较亮的像素变暗，较暗的像素变亮。这可以通过下面的公式表示：

   $$s=L-r$$

   其中，$ s $ 是输出像素的灰度级别，$ L $ 是灰度级别的最大值，$ r $ 是输入像素的灰度级别。这样的变换能够产生图像的底片效果，强调图像中原本较亮的区域。

2. 单位变换： 单位变换是一种线性变换，它保持图像的原始灰度级别不变。单位变换的公式如下：

   $$s=r$$

   这种变换并不改变图像的外观，但在图像增强中，它可能作为其他变换的基础或作为恢复操作的一部分。

这两种变换是线性的，因为它们都可以表示为输入像素值 $ r $ 与某个常数或者 $ L $的线性关系。线性变换是图像处理中一类简单而有效的操作，但对于一些更高级的增强技术，可能需要非线性的操作。

线性变换-负变换实现

void CMFCApplication1View::OnNegativetransform()
{// TODO: 在此添加命令处理程序代码if (gray_data != nullptr) {// 创建临时数组用于对比度拉伸处理unsigned char* neg_transformed_data = new unsigned char[bmpWidth * bmpHeight];// 负变换的处理代码for (int i = 0; i < bmpWidth * bmpHeight; ++i) {neg_transformed_data[i] = 255 - gray_data[i];}// 获取绘图设备CClientDC dc(this);CDC* pDC = &dc;// 绘制负变换后的灰度图m_pBmp->drawGrayBmp(pDC, neg_transformed_data, bmpWidth, bmpHeight, offset_left + 700, offset_top);// 在图片下方添加文字GdiplusStartupInput gdiplusStartupInput;ULONG_PTR gdiplusToken;GdiplusStartup(&gdiplusToken, &gdiplusStartupInput, nullptr);{Graphics graphics(pDC->m_hDC);Gdiplus::Font font(L"Arial", 12);SolidBrush brush(Color(255, 128, 0, 128));  // 文字颜色为紫色// 文字的位置PointF point(offset_left +700, offset_top + bmpHeight + 10);// 绘制文字graphics.DrawString(L"负变换后的灰度图", -1, &font, point, &brush);}GdiplusShutdown(gdiplusToken);// 释放负变换后的数据的内存delete[] neg_transformed_data;}else {// 处理图像未加载的情况AfxMessageBox(_T("未加载图片"));}
}

线性变换–负变换效果图

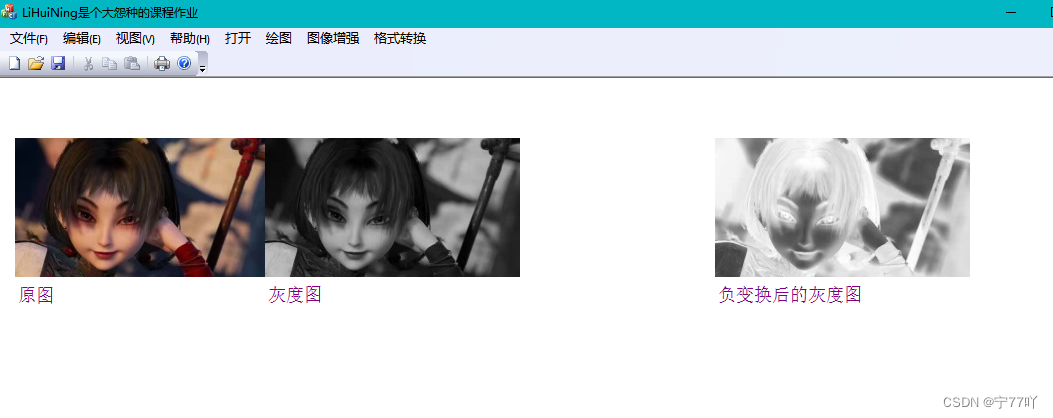
对数（对数和对数逆变换）

对数变换的原理

图像增强中的对数变换是一种常用的变换方法，它可以调整图像的灰度级分布，增强图像的对比度。对数变换的原理如下：

对数变换原理

对数变换的公式为：

$$s=c\cdot \log (1+r)$$

其中：

• s 是输出像素值（变换后的像素值），
• r 是输入像素值（原始像素值），
• c 是常数，用于调整变换的幅度。

对数变换的特点是对较低灰度级的输入像素值进行拉伸，对较高灰度级的像素值进行压缩，从而增强了图像的对比度。

对数逆变换原理

对数逆变换是对数变换的反操作，可以将经过对数变换的图像恢复到原始状态。对数逆变换的公式为：

$$r=\exp \left(\frac{s}{c}\right)-1$$

其中：

• $r$ 是原始像素值，
• $s$ 是经过对数变换后的像素值，
• $c$ 是与对数变换中的 $c$ 相同的常数。

对数逆变换的目的是使图像能够从经过对数变换的状态回到原始状态。

应用场景

对数变换常用于增强图像的低灰度级部分，特别是当图像的信息主要集中在较低灰度级时。例如，在医学图像处理中，对数变换常用于增强 X 射线图像的细节。

总体而言，对数变换适用于对比度较低的图像，能够提升图像的显示效果。

对数变换的实现

void CMFCApplication1View::OnLogtransform()
{// TODO: 在此添加命令处理程序代码if (gray_data != nullptr){// 创建临时数组用于对数变换处理unsigned char* log_transformed_data = new unsigned char[bmpWidth * bmpHeight];// 对数变换的处理代码const double c = 40.0;  // 可根据需要调整的常数for (int i = 0; i < bmpWidth * bmpHeight; ++i) {log_transformed_data[i] = static_cast<unsigned char>(c * log(1 + gray_data[i]));}// 获取绘图设备CClientDC dc(this);CDC* pDC = &dc;// 绘制对数变换后的灰度图m_pBmp->drawGrayBmp(pDC, log_transformed_data, bmpWidth, bmpHeight, offset_left , offset_top+ bmpHeight+50);// 在图片下方添加文字GdiplusStartupInput gdiplusStartupInput;ULONG_PTR gdiplusToken;GdiplusStartup(&gdiplusToken, &gdiplusStartupInput, nullptr);{Graphics graphics(pDC->m_hDC);Gdiplus::Font font(L"Arial", 12);SolidBrush brush(Color(255, 128, 0, 128));  // 文字颜色为紫色// 文字的位置PointF point(offset_left , offset_top + 2*bmpHeight+50);// 绘制文字graphics.DrawString(L"对数变换后的灰度图", -1, &font, point, &brush);}GdiplusShutdown(gdiplusToken);// 释放对数变换后的数据的内存delete[] log_transformed_data;}else {// 处理图像未加载的情况AfxMessageBox(_T("未加载图片"));}
}

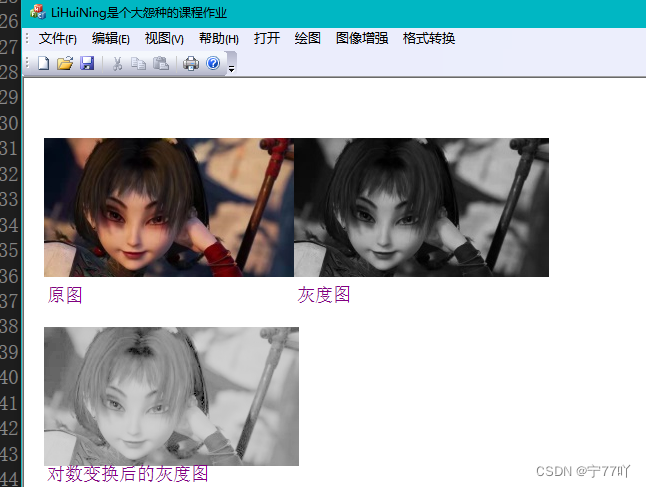
实现效果图

幂律（n次幂和n次根变换）

幂律（n次幂和n次根变换）的原理

幂律变换（Power Law Transformation）是一种图像增强的方法，通过对图像的像素值进行非线性映射来调整图像的对比度。该变换的一般形式如下：

$$g(x,y)=c\cdot [f(x,y){]}^{\gamma }$$

其中：

• $g(x,y)$ 是输出图像的像素值。
• $f(x,y)$ 是输入图像的像素值。
• $c$ 是常数，用于缩放输出的像素值范围。
• $\gamma$是幂律指数，控制像素值的非线性映射。

通过调整 $ \gamma $的值，可以实现不同程度的图像增强。当 $\gamma >1$ 时，会增强图像的高亮部分，降低暗部的对比度；而当$0<\gamma <1$ 时，会增强暗部的对比度，减小亮部的差异。

在实际应用中，一般会将$f(x,y)$ 归一化到 [0, 1] 的范围，应用变换后再将结果缩放到原图像的像素值范围。

幂律变换的应用场景包括调整图像的对比度、增强细节等。这种变换在图像处理和计算机视觉中经常用于图像增强的预处理阶段。

幂律（n次幂和n次根变换）的代码实现

//幂律（n次幂和n次根变换）
void CMFCApplication1View::OnPowerlawtransform()
{// TODO: 在此添加命令处理程序代码if (gray_data != nullptr) {// 创建临时数组用于幂律变换处理unsigned char* power_law_transformed_data = new unsigned char[bmpWidth * bmpHeight];double gamma = 2.0; // 幂律指数，可以根据需要调整// 幂律变换的处理代码for (int i = 0; i < bmpWidth * bmpHeight; ++i) {double normalized_pixel_value = static_cast<double>(gray_data[i]) / 255.0;double transformed_value = 255.0 * pow(normalized_pixel_value, gamma);power_law_transformed_data[i] = static_cast<unsigned char>(transformed_value);}// 获取绘图设备CClientDC dc(this);CDC* pDC = &dc;// 绘制幂律变换后的灰度图m_pBmp->drawGrayBmp(pDC, power_law_transformed_data, bmpWidth, bmpHeight, offset_left+250, offset_top + bmpHeight + 50);
}

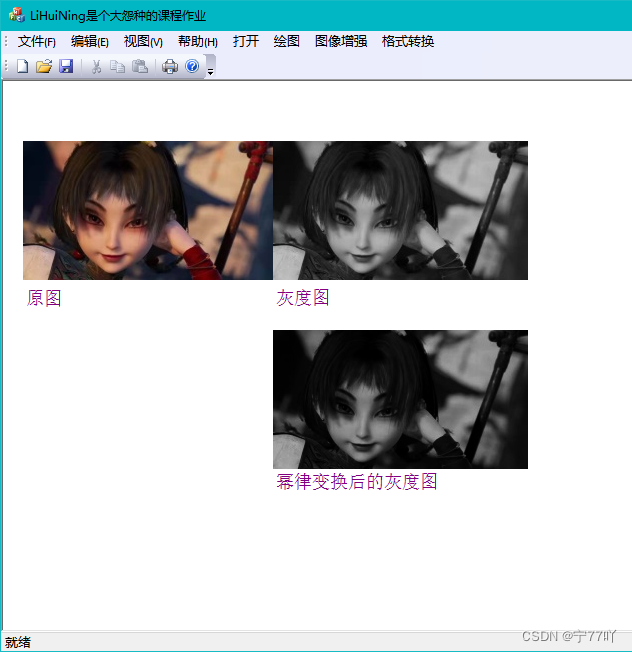
实现效果图