深度学习常见回归分支算法逐步分析，各种回归之间的优缺点，适用场景，举例演示

文章目录

1、线性回归（Linear Regression）
- 1.1 优点
- 1.2 缺点
- 1.3 适用场景
- 1.4 图例说明
2、多项式回归（Polynomial Regression）
- 2.1 优点
- 2.2 缺点
- 2.3 适用场景
- 2.4 图例说明
3、决策树回归（Decision Tree Regression）
- 3.1 优点
- 3.2 缺点
- 3.3 适用场景
4、随机森林回归（Random Forest Regression）
- 4.1 优点
- 4.2 缺点
- 4.3 适用场景
5、逻辑斯蒂回归（Logistic Regression）
- 5.1 优点
- 5.2 缺点
- 5.3 适用场景
6、弹性网络回归（Elastic Net Regression）
- 6.1 优点
- 6.2 缺点
- 6.3 适用场景
7、岭回归（Ridge Regression）
- 7.1 优点
- 7.2 缺点
- 7.3 适用场景
8、Lasso回归（Lasso Regression）
- 8.1 优点
- 8.2 缺点
- 8.3 适用场景

回归的概念：回归算法是一种用于预测连续数值输出的监督学习算法，可以根据输入特征预测一个或多个目标变量。它有多个分支，每个分支都有其独特的优缺点。下面是深度学习中几类回归变种：

1、线性回归（Linear Regression）

线性回归算法可以说是回归算法里面最简单的一种。

1.1 优点

简单且易于解释。
计算效率高，适用于大规模数据集。
在特征与目标之间存在线性关系时效果良好。

1.2 缺点

无法处理非线性关系。对于一些异常值，无法做到拟合曲线。
对异常值敏感。
需要满足线性回归假设（如线性关系、残差正态分布等）。

1.3 适用场景

适用场景：预测数值型目标，建立输入特征和输出之间的线性关系。
案例：预测房价。根据房屋特征（面积、卧室数量等），建立线性关系来估计房价。

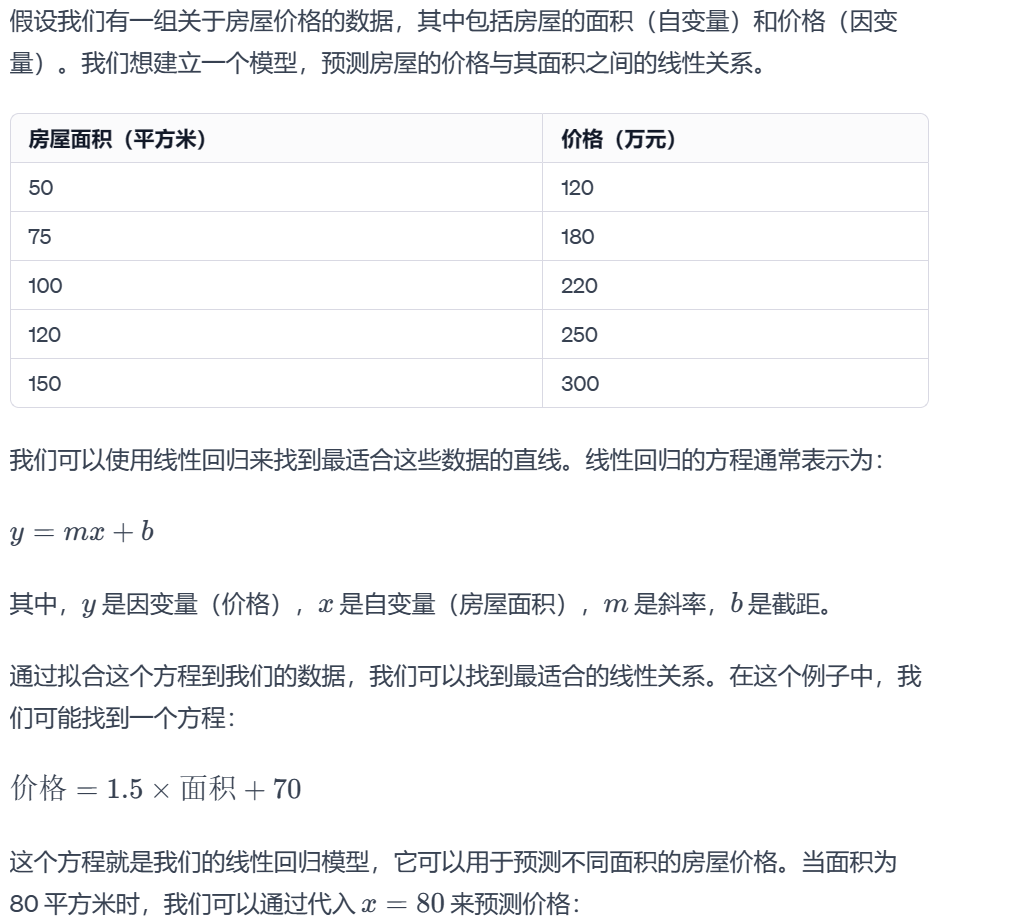
在这里插入图片描述

1.4 图例说明

代码：

import matplotlib.pyplot as plt
import numpy as np# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 数据
area = np.array([50, 75, 100, 120, 150])
price = np.array([120, 180, 220, 250, 300])# 执行线性回归
coefficients = np.polyfit(area, price, 1)
m, b = coefficients# 创建预测模型
predict_model = np.poly1d(coefficients)# 生成预测值
predicted_price = predict_model(area)# 绘制原始数据点
plt.scatter(area, price, label='实际数据点')# 绘制线性回归线
plt.plot(area, predicted_price, label=f'线性回归: y = {m:.2f}x + {b:.2f}', color='red')# 添加标签和图例
plt.xlabel('房屋面积（平方米）')
plt.ylabel('价格（万元）')
plt.title('线性回归')
plt.legend()
# 显示图形
plt.show()

生成对应图像：
在这里插入图片描述
深度学习中的线性回归
代码：

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 生成模拟数据
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)# 转换为PyTorch的Tensor
X_tensor = torch.from_numpy(X).float()
y_tensor = torch.from_numpy(y).float()# 定义线性回归模型
class LinearRegressionModel(nn.Module):def __init__(self, input_size, output_size):super(LinearRegressionModel, self).__init__()self.linear = nn.Linear(input_size, output_size)def forward(self, x):return self.linear(x)# 实例化模型
input_size = 1
output_size = 1
model = LinearRegressionModel(input_size, output_size)# 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)# 训练模型
num_epochs = 100
for epoch in range(num_epochs):# Forward passoutputs = model(X_tensor)loss = criterion(outputs, y_tensor)# Backward pass and optimizationoptimizer.zero_grad()loss.backward()optimizer.step()# 打印训练过程中的损失if (epoch+1) % 10 == 0:print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')# 绘制模型预测结果和真实数据
predicted = model(X_tensor).detach().numpy()
plt.scatter(X, y, label='实际数据点')
plt.plot(X, predicted, label='模型预测', color='red')
plt.xlabel('房屋面积（平方米）')
plt.ylabel('价格（万元）')
plt.title('线性回归')
plt.legend()
plt.show()

生成对应的图像：
在这里插入图片描述
是不是看着比简单的回归复杂很多，深度模型解决的回归问题还要比这复杂得多。

2、多项式回归（Polynomial Regression）

2.1 优点

可以捕捉特征和目标之间的非线性关系。
相对简单实现。

2.2 缺点

可能会过度拟合数据，特别是高阶多项式。
需要选择适当的多项式阶数。

2.3 适用场景

适用场景：处理非线性关系，通过添加多项式特征来拟合曲线。
案例：预测股票价格。使用多项式回归来拟合价格与时间之间的非线性关系。

2.4 图例说明

代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 生成模拟数据
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)# 选择多项式次数
degree = 2# 构建设计矩阵
poly_features = PolynomialFeatures(degree=degree, include_bias=False)
X_poly = poly_features.fit_transform(X)# 使用线性回归拟合多项式特征
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)# 预测
X_new = np.linspace(0, 2, 100).reshape(-1, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)# 绘制结果
plt.scatter(X, y, label='True data')
plt.plot(X_new, y_new, 'r-', label='Predictions', linewidth=2)
plt.xlabel('X')
plt.ylabel('y')
plt.title('多项式线性回归')
plt.legend()
plt.show()# 评估模型
y_pred = lin_reg.predict(X_poly)
mse = mean_squared_error(y, y_pred)
print(f'Mean Squared Error: {mse:.4f}')