霍夫曼编码的原理就是根据字符的使用频率,排成二叉树,使用次数少的放到后面,使用次数多的离根节点越近;这样字符的占位也相应的较少。
- 首先,主要操作是找每次字符中使用频率最低的(数最小)两个数字,然后将他们两个结合;
- 结合后的数字和添加到原数组中(使用频率次数中),继续找最小的两个,根据左小右大原则存放;
- 最终组成的数从根节点开始左0右1,遍历到目标节点即为哈夫曼编码。
其中,如果遇到相等的情况则按小于的情况来看。
以下题为例,画哈夫曼编码图

第一步
先写出字符对应的频率:

找到其中最小的两个数,目前为5和4;并将他们两个结合左小右大,4+5=9;
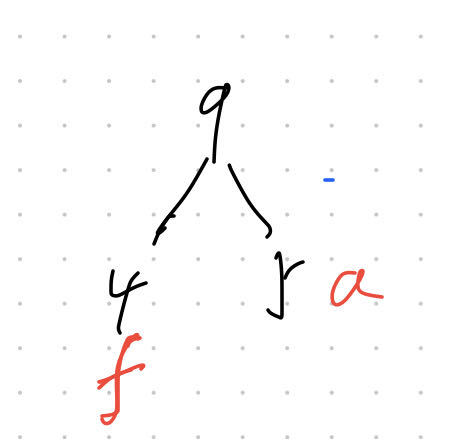
第二步
将9写入原序列中,删除已经用掉的4和5
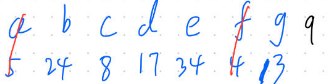
再找其中最小的两个数,这次为8和9;9已经在图中了,根据左小右大原则,8放到9的左边并相加结合;
8+9=17
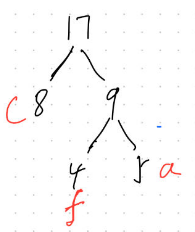
第三步
基本就是这样的步骤,下面删除已经用过的8和9,再加上17

当前最小的数为13和17(注意相同的数字优先找原序列中的),找个其他地方重新结合即可;
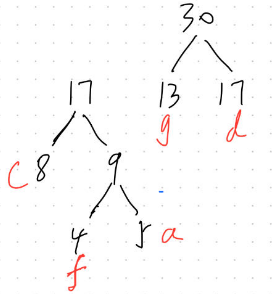
第四步
数字序列中加上刚刚得到的30,找到最小的17和24结合;
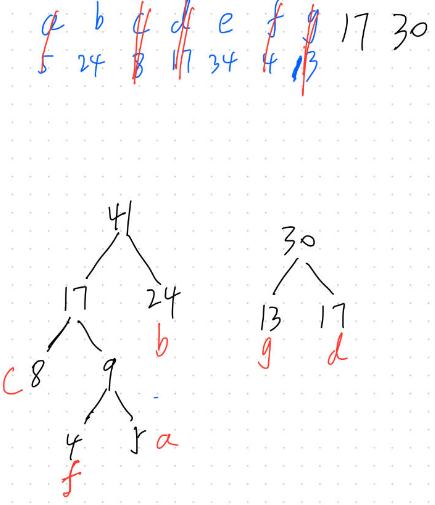
第五步
这一步最小的数为34和30,将这两个结合,得到30+34=64;
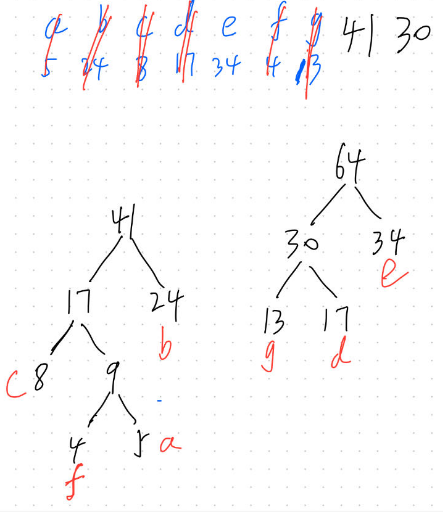
第六步
将最后两个数结合即可得到哈夫曼树;
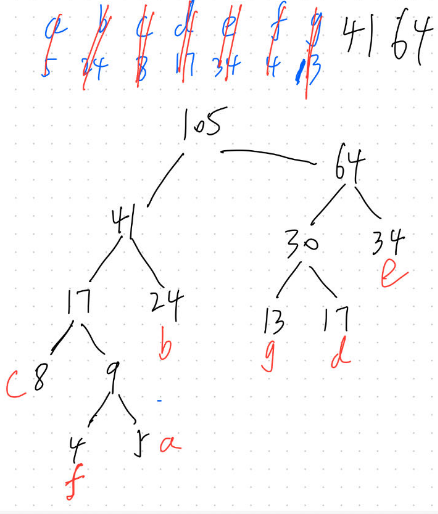
以下方法是2022年底有缺陷的方法。
直接上题目:
已知字符集{ a, b, c, d, e, f },若各字符出现的次数分别为{ 6, 3, 8, 2, 10, 4 },则对应字符集中各字符的哈夫曼编码可能是:(2分)
A. 00, 1011, 01, 1010, 11, 100
B. 00, 100, 110, 000, 0010, 01
C. 10, 1011, 11, 0011, 00, 010
D. 0011, 10, 11, 0010, 01, 000
步骤一:
1.找最小两个次数(这里是2和3)

2.把他们放进树中(小左大右)
3.每次组合都多一个父节点(即2+3=5)
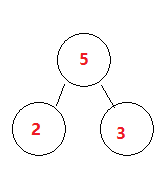
步骤二:
1.再选出2个最小的数(排除上面已经选了的)——选出了4和6

2.因为4<=5(注意是小于等于) , 6>5(5为步骤一中组合后的父节点)
3.单独拿4来跟5组合(小左大右) 【如果拿出的2个数都比5小,则这2个数自己组合后跟5组合,下面提到】
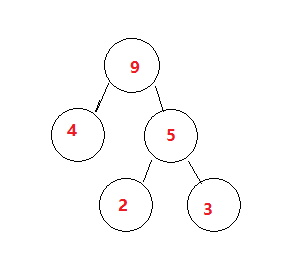
步骤三:
1.因为步骤二用掉了4,还没用6。现在取最小2个数

2.因为6 < 9 , 8< 9 所以6和8自己组合(小左大右) (组合后先放一边)
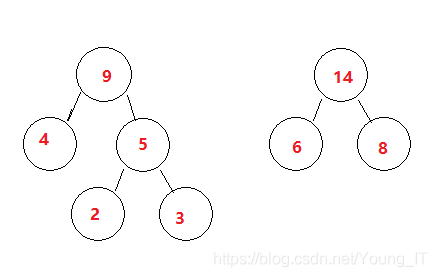
步骤四:
1.取出最后10

2.10要和这两个子树根节点最小的组合(9<14,所以和9组合)(小左大右)
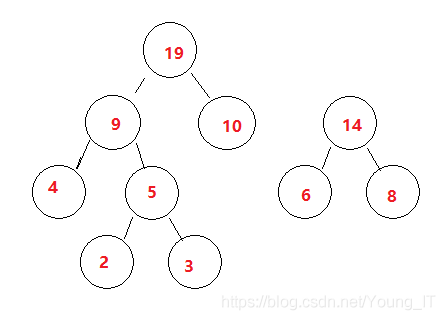
3.然后把14的子树组合上去(小左大右) 所以放左边
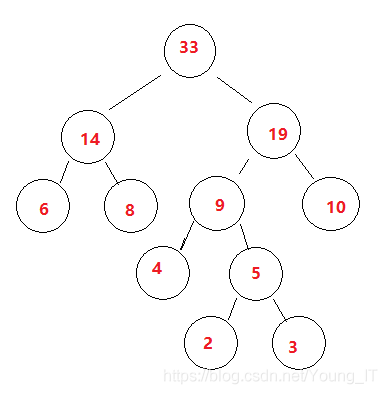
步骤五:
组合完哈夫曼树后,将对应的字符填上去
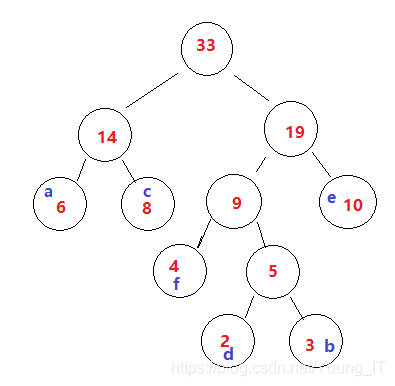
步骤六:
从根节点开始向下走往左为0,往右1。走到对应的字符的路径就是该字符的哈夫曼编码(左0右1)
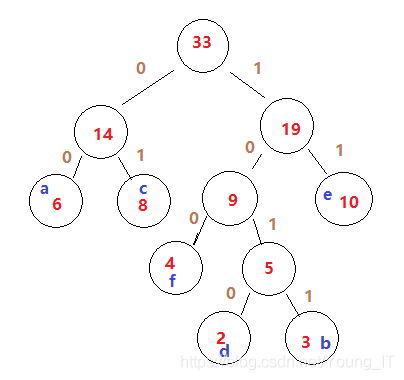
最后结果:
| 字符 | 哈夫曼编码 |
|---|---|
| a | 00 |
| b | 1011 |
| c | 01 |
| d | 1010 |
| e | 11 |
| f | 100 |
所以最后答案 A
已知字符集{ a, b, c, d, e, f },若各字符出现的次数分别为{ 6, 3, 8, 2, 10, 4 },则对应字符集中各字符的哈夫曼编码可能是:(2分)
A. 00, 1011, 01, 1010, 11, 100 ✔
B. 00, 100, 110, 000, 0010, 01
C. 10, 1011, 11, 0011, 00, 010
D. 0011, 10, 11, 0010, 01, 000





)
)





)



 举例说明)
使用说明)

