这篇文章将介绍如何使用python来实现FMCW工作原理的仿真,第1章内容将介绍距离检测原理,第2章内容会介绍速度检测原理。
第1章
第1部分: 距离检测原理
调制的连续波雷达通常也被叫做调频连续波(FMCW)雷达是一个使用频率调制来测量目标的距离的系统。在频率调制中,电磁波的频率随时间线性增加。或者说,发射频率会以恒定速率改变。这种频率随着时间线性增加的信号被称为chirp。FMCW系统测量发射信号和反射信号频率的瞬时差异δf,这直接和反射的chirp的时间差成比例。这个时间差能用来计算目标的距离。
下图(左)显示了一个chirp频率随时间变化的表现,右边显示频率随时间线性增加的chirp的幅度随时间变化图。

雷达前面的单目标产生的中频信号是一个固定频率音调,这个频率由下式给出:
IF(frequency) = 2S*d / c
这里d是目标到雷达的距离,单位m,c是光速,m/s,S是chirp斜率,由chirp持续时间内带宽的变化率得到。因此,我们可以对中频信号做FFT得到频率,再通过测量频率来计算距离。
第2部分:Python仿真
第1步: 雷达参数设置,这一步会设置雷达系统的基本参数
maxR = 200 # Maximum range
rangeRes = 1 # Range resolution
maxV = 70 # Maximum speed
fc = 77e9 # Carrier frequency
c = 3e8 # Speed of lightr0 = 100 # Target distance
v0 = 70 # Target speedB = c/(2*rangeRes) # Bandwidth
Tchirp = 5.5*2*maxR/c # Chirp time
endle_time = 6.3e-6
slope = B/Tchirp # Chirp slope
f_IFmax = (slope*2*maxR)/c # Maximum IF frequency
f_IF = (slope*2*r0)/c # Current IF frequencyNd = 128 # Number of chirp
Nr = 1024 # Number ADC sampling points
vres = (c/fc)/(2*Nd*(Tchirp + endle_time)) # Speed resolution
Fs = Nr/Tchirp # Sampling rate第2步: 发射信号, 假设发射的是cos信号,频率随时间线性变化
t = np.linspace(0, Nd*Tchirp, Nr*Nd) # Time of Tx and Rx
angle_freq = fc*t+(slope*t*t)/2 # Tx signal angle speed
freq = fc + slope * t # Tx frequency
Tx = np.cos(2*np.pi*angle_freq) # Waveform of Tx
plt.subplot(3,3,1)
plt.plot(t[0:Nr],Tx[0:Nr])
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('Tx Signal')
plt.subplot(3,3,2)
plt.plot(t[0:Nr],freq[0:Nr])
plt.xlabel('Time')
plt.ylabel('Frequency')
plt.title('Tx F-T')r0 = r0 + v0*t第3步: 接收信号, 接收波形可以从发射波形和时延计算
td = 2*r0/c
tx = t
freqRx = fc + slope*(t)
Rx = np.cos(2*np.pi*(fc*(t-td) + (slope*(t-td)*(t-td))/2))
plt.subplot(3,3,3)
plt.plot(t[0:Nr],Rx[0:Nr])
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('Rx Signal')
plt.subplot(3,3,4)
plt.plot(t[0:Nr]+td[0:Nr],freqRx[0:Nr])
plt.xlabel('Time')
plt.ylabel('Frequency')
plt.title('Chirp F-T')第4步: 中频信号,根据处理,假设中频信号可以用cos((2*pi*wt*t-2*pi*wr*t))表示
IF_angle_freq = fc*t+(slope*t*t)/2 - ((fc*(t-td) + (slope*(t-td)*(t-td))/2))
freqIF = slope*td
IFx = np.cos(-(2*np.pi*(fc*(t-td) + (slope*(t-td)*(t-td))/2)) + (2*np.pi*angle_freq))
plt.subplot(3,3,5)
plt.plot(t[0:Nr],IFx[0:Nr])
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('IFx Signal')第5步: 中频信号FFT, 这一步, 我们通过对中频信号做FFT计算中频信号的频率
doppler = 10*np.log10(np.abs(np.fft.fft(IFx[0:Nr])))
frequency = np.fft.fftfreq(Nr, 1/Fs)
range = frequency*c/(2*slope)
plt.subplot(3,3,6)
plt.plot(range[0:int(Nr/2)],doppler[0:int(Nr/2)])
plt.xlabel('Frequency->Distance')
plt.ylabel('Amplitude')
plt.title('IF Signal FFT')第6步: 时间频谱图, 这一步, 计算频谱随时间变化图
# 2D plot
plt.subplot(3,3,7)
plt.specgram(IFx,Nr,Fs)
plt.xlabel('Time')
plt.ylabel('Frequency')
plt.title('Spectogram')我们可以看到,在单个帧周期内,由于目标位移引起的中频信号频率变化在频谱图中很难区分,因此我们需要通过相位变化来检测小的位移和速度。

第2章
第1部分:速度检测原理
如第1章末尾所说,小尺度移动很难由距离频率关系检测,如下图所示,在帧周期内,不能在频谱中找到明显的移动。另外,如果多个目标在相同的距离,我们不能通过距离频率关系区分他们,因为他们在频谱中有着相同的中频频率。然而,我们可以通过测量中频信号的相位变化来检测这些小尺度移动,区分不同的目标。通过相位变化做速度估计的基本想法如下所示:

第1步: 速度维度数据提取
每个chirp提取一个采样点,对于Nd个chirp的帧,将会有Nd个点的列表。
chirpamp = []
chirpnum = 1
while(chirpnum <= Nd):start = (chirpnum - 1)*Nrend = chirpnum*Nrchirpamp.append(IFx[start])chirpnum = chirpnum + 1第2步: 对相位变化和速度做速度维度FFT
doppler = 10*np.log10(np.abs(np.fft.fft(chirpamp)))
FFTfrequency = np.fft.fftfreq(Nd,1/Fs)
velocity = 5*np.arange(0,Nd)/3
plt.subplot(3,3,8)
plt.plot(velocity[0:int(Nd/2)],doppler[0:int(Nd/2)])
plt.xlabel('Velocity')
plt.ylabel('Amplitude')
plt.title('IF Velocity FFT')
第3步:2维FFT和速度距离关系
mat2D = np.zeros((Nd,Nr))
i = 0
while(i < Nd):mat2D[i,:] = IFx[i*Nr:(i+1)*Nr]i = i + 1
# plt.matshow(mat2D)
# plt.title('Original data')
Z_fft2 = abs(np.fft.fft2(mat2D))
Data_fft2 = Z_fft2[0:int(Nd/2),0:int(Nr/2)]
plt.subplot(3,3,9)
plt.imshow(Data_fft2)
plt.xlabel('Range')
plt.ylabel('Velocity')
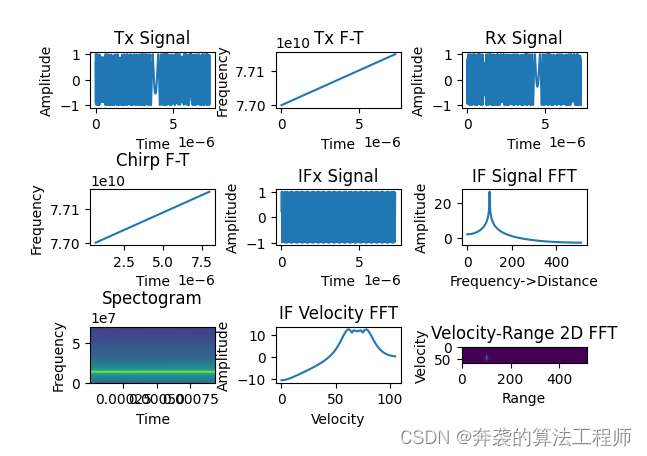
plt.title('Velocity-Range 2D FFT')然后,设置结果显示和图片保存,就能得到仿真结果了。
plt.tight_layout(pad=3,w_pad=0.05,h_pad=0.05)
#plt.savefig('simulate.png', bbox_inches='tight', pad_inches=0.3) # 紧凑型,留白较少
plt.show()
最后,别忘了代码最开始导入库文件,这样才能保证代码运行正常。
import numpy as np
import matplotlib.pyplot as plt
from numpy import fft
from mpl_toolkits.mplot3d import Axes3D