关卡名	理解树的特征	我会了✔️
内容	1.理解树的结构、基本概念、性质以及存储方式	✔️
	2.理解树的前中后三种遍历方式	✔️
	3.理解如何使用前中序列和中后序列来构造树	✔️

1 树的常见概念 

树是一个有n个有限节点组成一个具有层次关系的集合，每个节点有0个或者多个子节点，没有父节点的节点称为根节点，也就是说除了根节点以外每个节点都有父节点，并且有且只有一个。树的种类比较多，我们最常见的应该是二叉树了，基本结构如下：

参考上面的结构，可以很方便的理解树的如下概念：

1. 节点的度:一个节点含有的子节点的个数称为该节点的度;
2. 树的度:一棵树中，最大的节点的度称为树的度，注意与节点度的区别；
3. 叶节点或终端节点:度为0的节点称为叶节点;
4. 非终端节点或分支节点:度不为0的节点;
5. 双亲节点或父节点:若一个节点含有子节点，则这个节点称为其子节点的父节点;
6. 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
7. 兄弟节点:具有相同父节点的节点互称为兄弟节点;
8. 节点的祖先:从根到该节点所经分支上的所有节点;
9. 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
10. 森林:由m(m>=0)棵互不相交的树的集合称为森林;
11. 无序树:树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树;
12. 有序树:树中任意节点的子节点之间有顺序关系，这种树称为有序树;
13. 二叉树:每个节点最多含有两个子树的树称为二叉树;

2 树的性质

性质1: 在二叉树的第i层上至多有2^(i-1)个结点（i>0）
性质2: 深度为k的二叉树至多有2^k - 1个结点（k>0）
性质3: 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1;
性质4:具有n个结点的完全二叉树的深度必为 log2(n+1)
性质5:对完全二叉树，若从上至下、从左至右编号，则编号为i 的结点，其左孩子编号必为2i，
其右孩子编号必为2i＋1；其双亲的编号必为i/2（i＝1 时为根,除外）
满二叉树和完全二叉树是经常晕的问题，我们有必要单独看一下。满二叉树就是如果一棵二叉树只有度为0的节点和度为2的节点，并且度为0的节点在同一层上，则这棵二叉树为满二叉树。

这棵二叉树为满二叉树，也可以说深度为k=4，有2^k-1=15个节点的二叉树。
完全二叉树的定义如下:在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大 值，并且最下面一层的节点都集中在该层最左边的若干位置。
这个定义最邪乎了，估计大部分看了之后还是不懂什么是完全二叉树，看这个图就知道了：

前面两棵树的前n-1层都是满的，最后一层所有节点都集中在左侧区域，而且节点之间不能有空隙。最后一个为什么不是？因为有一节点缺了一个左子节点。

3 树的定义与存储方式

注意
本关讲义我们主要看原理，不写可执行的代码，因此我们只用伪码，不提供各种语言的定义

定义树的原理与前面讲的链表本质上是一样的，只不过多了一个指针，如果是二叉树，只要在链表的定义上增加一个指针就可以了：

定义二叉树

public class TreeNode {

        int val;

        TreeNode left;

        TreeNode right;

}

这里本质上就是有两个引用，分别指向两个位置，为了便于理解，我们分别命名为左孩子和右孩子。如果是N叉树该如何定义呢？其实就是每个节点最多可以有N个指针指向其他地方，这是不用left和right，使用一个List就可以了，也就是： 

定义N叉树

public class TreeNode {

        int val;

        List<TreeNode> nodes;

}

那能否用数组来存储二叉树呢?其实就是用数组来存储二叉树，顺序存储的方式如图:

用数组来存储二叉树如何遍历的呢?如果父节点的数组下表是i，那么它的左孩子就是i * 2 + 1，右孩子就是 i * 2 + 2。但是用链式表示的二叉树，更有利于我们理解，所以一般我们都是用链式存储二叉树。所以大家要了解，用数组依然可以表示二叉树。
使用数组存储的最大不足是可能存在大量的空间浪费。例如上图中如果b分支没有，那么数组种1 3 4 位置都要空着，但是整个数组的大小仍然是7，因此很少使用数组来存储树。

4 树的遍历方式

我们现在就来看一下树的常见遍历方法。二叉树的遍历方式有层次遍历和深度优先遍历两种:

• 深度优先遍历:先往深走，遇到叶子节点再往回走。
• 广度优先遍历:一层一层的去遍历，一层访问完再访问下一层。

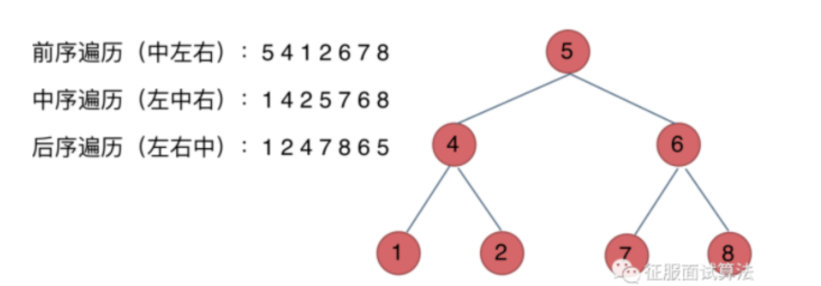
这两种遍历方式不仅仅是二叉树，N叉树也有这两种方式的，图结构也有，只不过我们更习惯叫广度优先和深度优先，本质是一回事。深度优先又有前中后序三种， 有同学总分不清这三个顺序，问题就在不清楚这里前中后是相对谁来说的。记住一点：前指的是中间的父节点在遍历中的顺序，只要大家记住 前中后序指的就是中间节点的位置就可以了。
看如下中间节点的顺序，就可以发现，访问中间节点的顺序就是所谓的遍历方式
前序遍历:中左右
中序遍历:左中右
后序遍历:左右中
大家可以对着如下图，看看自己理解的前后中序有没有问题。 

后面大量的算法都与这四种遍历方式有关，有的题目根据处理角度不同 ，可以用层次遍历，也可以用一种甚至两种深度优先的方式来实现。

5 通过序列构造二叉树

前面我们已经介绍了前中后序遍历的基本过程，现在我们看一下如何通过给出的序列来恢复原始二叉树，看三个序列：
(1) 前序：1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2) 中序：3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
(3) 后序：8 7 6 5 4 3 2 10 15 14 13 12 11 9 1

5.1 前中序列复原二叉树

我们先看如何通过前中序列复原二叉树：
(1) 前序：1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2) 中序：3 4 8 6 7 5 2 1 10 9 11 15 13 14 12

• 第一轮：

我们知道前序第一个访问的就是根节点，所以根节点就是1。
中序遍历的特点是根节点的左子树的元素都在根节点的左侧，右子树的元素都在根节点的右侧，从中序遍历序列我们可以划分成如下结构：

中序序列划分：

[3 4 8 6 7 5 2] 1[ 10 9 11 15 13 14 12]

前序序列划分为：

1 [2 3 4 5 6 8 7 ] [9 10 11 12 13 15 14]

上面前序序列第一个括号里的都是左子树的元素，第二个括号一定都是右子树的元素。
那这里怎么知道两个括号从哪里分开呢？是参照中序的两个数组划分的。我们看到前序中7之前的元素都在中序第一个数组中，9之后的所有元素就在第二个数组种，所以我们从7和9之间划分。
由此，画图表示一下此时知道的树的结构为：

• 第二轮：

我们先看两个序列的第一个数组：
前序：2 3 4 5 6 8 7 中序：3 4 8 6 7 5 2
此时又可以利用上面的结论划分了：根节点是2，然后根据2在中序中的位置可以划分为：

前序：2 [3 4 5 6 8 7 ]

中序：[3 4 8 6 7 5 ] 2

所以此时的树结构为：

• 第三轮：

对 3 4 5 6 8 7 继续划分：前序：3 [4 5 6 8 7 ] 中序：3 [4 8 6 7 5 ]此时结构为：

• 第四轮 :

对 4 5 6 8 7 继续划分：前序：4 [5 6 8 7 ] 中序：4 [8 6 7 5 ]

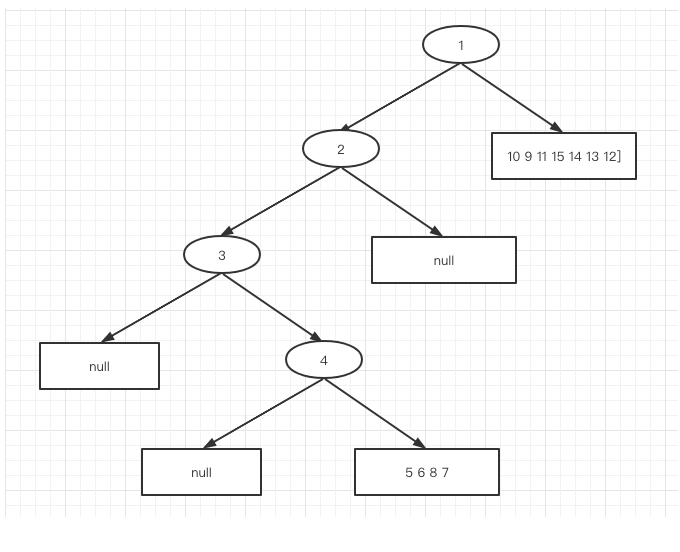
此时树为：

• 第五轮：对 5 6 8 7 继续划分：前序：5 [6 8 7 ] 中序：[8 6 7 ] 5

这个题有点恶心，每次只能确定一个元素，道理是这样子，直接画最终结果吧：

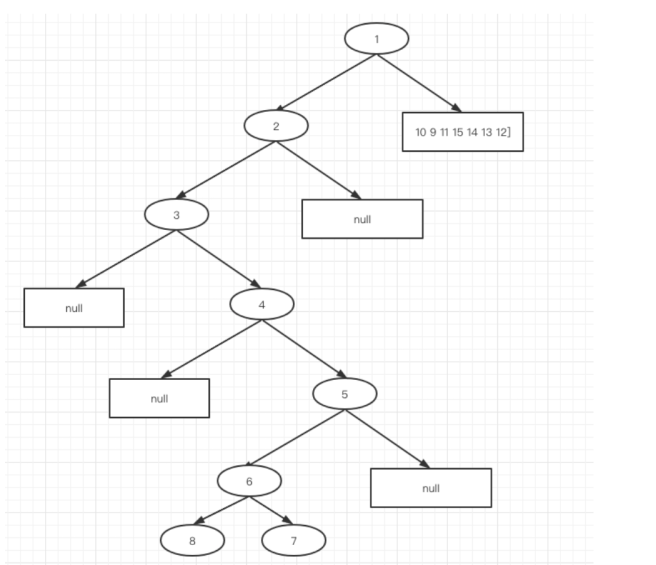
这个图有点丑，我们将空节点都去掉就是这样了：

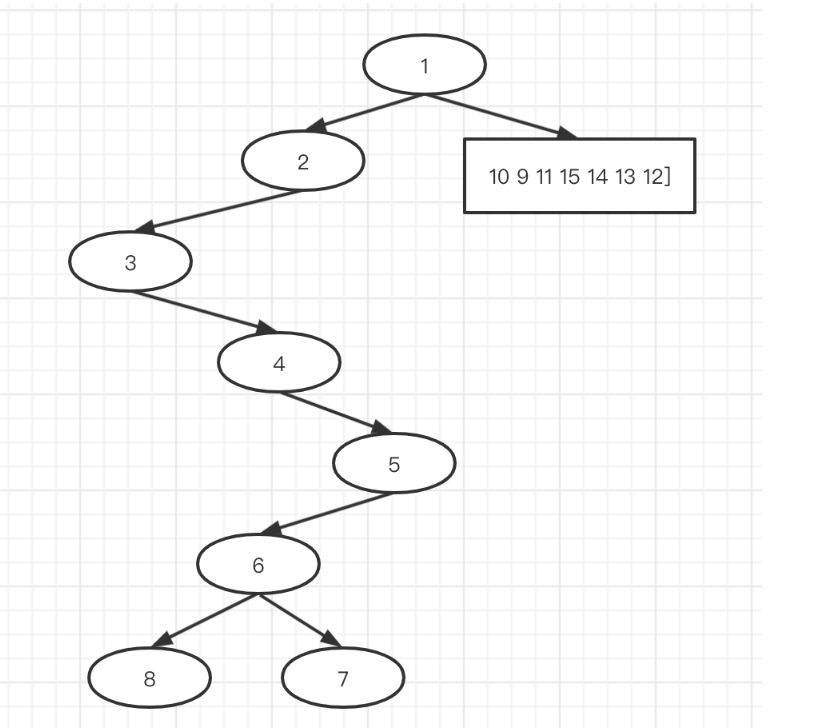
同理，对于序列[ 10 9 11 15 13 14 12]，我们也可以逐步划分，这个请读同学自己试一试，最终结果为：

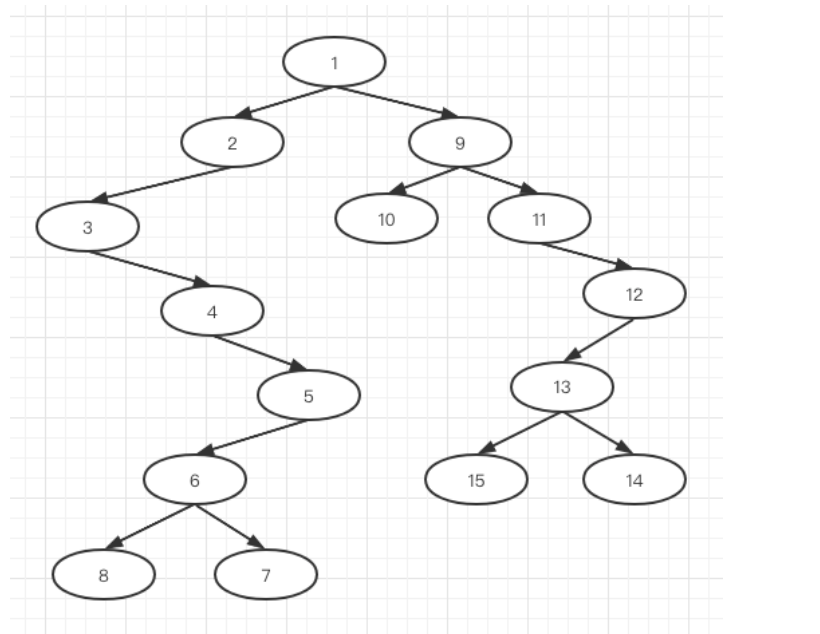
5.2 通过中序和后序序列恢复二叉树

通过中序和后序也能恢复原始序列的，唯一的不同是后序序列的最后一个是根节点，中序的处理也是上面一样的过程：

• 前序：1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
• 中序：3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
• 后序：8 7 6 5 4 3 2 10 15 14 13 12 11 9 1

读者可以自行试一试，我们就不再赘述。
问题：为什么前序和后序不能恢复二叉树
既然上面两种都行，那为什么前序和后序不行呢？我们看上面的例子： 

(1) 前序：1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2) 后序：8 7 6 5 4 3 2 10 15 14 13 12 11 9 1
根据上面的说明，我们通过前序可以知道根节点是1，通过后序也能知道根节点是1，但是中间是怎么划分的呢？其他元素哪些属于左子树，哪些属于右子树呢？很明显通过两个序列都不知道，所以前序和后序序列不能恢复二叉树。
如果将上述过程用代码实现该怎么做呢？通过前序和中序构造树就是LeetCode105题，通过中序和后序构造树就是LeetCode106题，实现过程略微繁琐，感兴趣的同学可以研究一下。