文章目录
- 一【题目类别】
- 二【题目难度】
- 三【题目编号】
- 四【题目描述】
- 五【题目示例】
- 六【题目提示】
- 七【解题思路】
- 八【时间频度】
- 九【代码实现】
- 十【提交结果】
一【题目类别】
- 矩阵
二【题目难度】
- 简单
三【题目编号】
- 1572.矩阵对角线元素的和
四【题目描述】
- 给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。
- 请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。
五【题目示例】
-
示例 1:
-
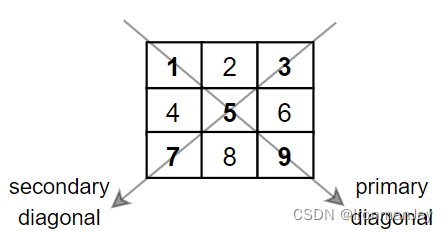
-
输入:mat = [[1,2,3],
[4,5,6],
[7,8,9]] -
输出:25
-
解释:对角线的和为:1 + 5 + 9 + 3 + 7 = 25。请注意,元素 mat[1][1] = 5 只会被计算一次。
-
-
示例 2:
- 输入:mat = [[1,1,1,1],
[1,1,1,1],
[1,1,1,1],
[1,1,1,1]] - 输出:8
- 输入:mat = [[1,1,1,1],
-
示例 3:
- 输入:mat = [[5]]
- 输出:5
六【题目提示】
- n = = m a t . l e n g t h = = m a t [ i ] . l e n g t h n == mat.length == mat[i].length n==mat.length==mat[i].length
- 1 < = n < = 100 1 <= n <= 100 1<=n<=100
- 1 < = m a t [ i ] [ j ] < = 100 1 <= mat[i][j] <= 100 1<=mat[i][j]<=100
七【解题思路】
- 定义i遍历二维数组的行数,j遍历二维数组的列数
- 如果i==j,说明是主对角线的元素
- 如果i+j==n-1,说明是副对角线的元素
- 采用
||进行判断,这样就不会将主对角线和副对角线的元素多加一次,因为只遍历了一次数组 - 然后将其求和,最后返回结果即可
八【时间频度】
- 时间复杂度: O ( n 2 ) O(n^2) O(n2), n n n为传入的正方形数组的长度
- 空间复杂度: O ( 1 ) O(1) O(1)
九【代码实现】
- Java语言版
class Solution {public int diagonalSum(int[][] mat) {int n = mat.length;int res = 0;for(int i = 0;i < n;i++){for(int j = 0;j < n;j++){if(i == j || i + j == n - 1){res += mat[i][j];}}}return res;}
}
- C语言版
int diagonalSum(int** mat, int matSize, int* matColSize)
{int n = matSize;int res = 0;for(int i = 0;i < n;i++){for(int j = 0;j < n;j++){if(i == j || i + j == n - 1){res += mat[i][j];}}}return res;
}
- Python语言版
class Solution:def diagonalSum(self, mat: List[List[int]]) -> int:n = len(mat)res = 0for i in range(0,n):for j in range(0,n):if i == j or i + j == n - 1:res += mat[i][j]return res
- C++语言版
class Solution {
public:int diagonalSum(vector<vector<int>>& mat) {int n = mat.size();int res = 0;for(int i = 0;i < n;i++){for(int j = 0;j < n;j++){if(i == j || i + j == n - 1){res += mat[i][j];}}}return res;}
};
十【提交结果】
-
Java语言版
-
C语言版
-
Python语言版
-
C++语言版
)
)
sd整合包v4.2 版本安装说明)
)



软件工程基础知识)




,但是pycharm的terminal中无法使用。)




- 命令启动appium之 appium服务命令行参数(超详解))

