文章目录
- 目的:用python实现two way ANOVA 双因素方差分析
- 1. python代码实现
- 1 加载python库
- 2 加载数据
- 3 统计样本重复次数,均值和方差,绘制箱线图
- 4 查看people和group是否存在交互效应
- 5 模型拟合与Two Way ANOVA:双因素方差分析
- 6 多重比较,post hoc t-tests
- 7 计算效应量Correlation family: η^2、ω^2 (适用于 Correlational data)
- 2. 双因素方差分析理论和公式
- 3. 效应量分析
目的:用python实现two way ANOVA 双因素方差分析
1. python代码实现

1 加载python库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats from statsmodels.formula.api import ols # 最小二乘法拟合
from statsmodels.stats.anova import anova_lm # 方差分析
from statsmodels.stats.multicomp import pairwise_tukeyhsd # post Hoc t_test
2 加载数据
value(month):治疗2周的各类被试的血糖值
group(PhysicalTherapy):表示有两种治疗方案,sham组(1)和rTMS组(2)
people(PsychiatricTreatment):表示有3种被试,年轻健康组(3)、老年健康组(1)、老年患病组(2)
df = pd.read_excel('data//TMS_demoData1.xlsx')
data = pd.DataFrame(df)
data.head(24)
| value | group | people | |
|---|---|---|---|
| 0 | 11.0 | 1 | 1 |
| 1 | 9.4 | 1 | 2 |
| 2 | 12.5 | 1 | 3 |
| 3 | 9.6 | 1 | 1 |
| 4 | 9.6 | 1 | 2 |
| 5 | 11.5 | 1 | 3 |
| 6 | 10.8 | 1 | 1 |
| 7 | 9.6 | 1 | 2 |
| 8 | 10.5 | 1 | 3 |
| 9 | 10.5 | 1 | 1 |
| 10 | 10.8 | 1 | 2 |
| 11 | 12.5 | 1 | 3 |
| 12 | 10.5 | 2 | 1 |
| 13 | 10.8 | 2 | 2 |
| 14 | 10.5 | 2 | 3 |
| 15 | 11.5 | 2 | 1 |
| 16 | 10.5 | 2 | 2 |
| 17 | 11.8 | 2 | 3 |
| 18 | 12.0 | 2 | 1 |
| 19 | 10.5 | 2 | 2 |
| 20 | 11.5 | 2 | 3 |
| 21 | 11.8 | 2 | 1 |
| 22 | 10.2 | 2 | 2 |
| 23 | 11.5 | 2 | 3 |
3 统计样本重复次数,均值和方差,绘制箱线图
data.describe()
| value | group | people | |
|---|---|---|---|
| count | 24.000000 | 24.000000 | 24.000000 |
| mean | 10.891667 | 1.500000 | 2.000000 |
| std | 0.889512 | 0.510754 | 0.834058 |
| min | 9.400000 | 1.000000 | 1.000000 |
| 25% | 10.500000 | 1.000000 | 1.000000 |
| 50% | 10.800000 | 1.500000 | 2.000000 |
| 75% | 11.500000 | 2.000000 | 3.000000 |
| max | 12.500000 | 2.000000 | 3.000000 |
fig, ax = plt.subplots(1,2,figsize=(12,6),dpi=600) # 1行2列的子图
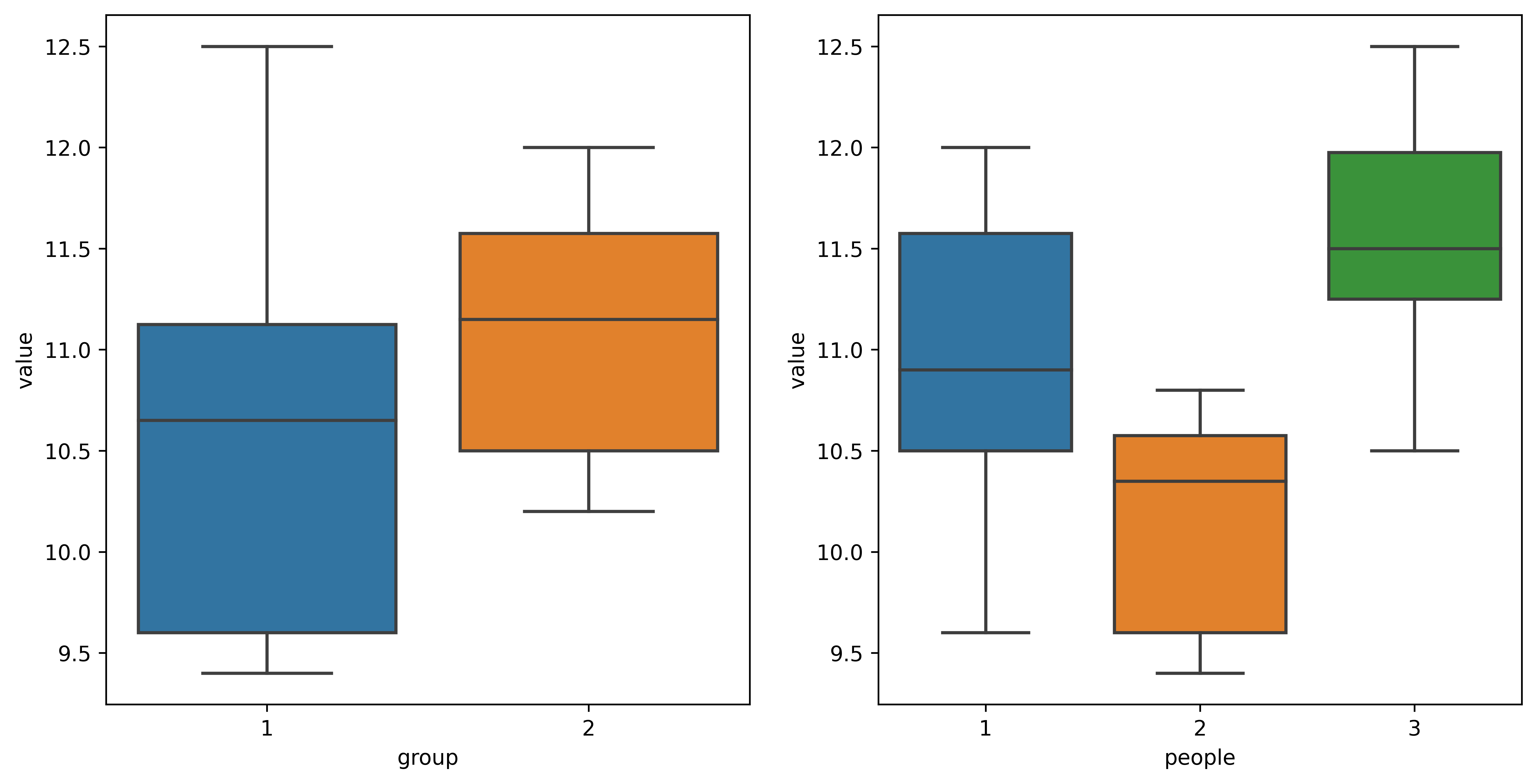
sns.boxplot(x = 'group', y = 'value', data = data, ax = ax[0])
sns.boxplot(x = 'people', y = 'value', data = data, ax = ax[1])## 可以看出rTMS组的血糖水平sham组的高,因此我们得看这是由于治疗方案引起的还是由于随机误差引起的
## 即从试验结果推断,因素 group 对试验结果有无显著影响,即当 group 取不同水平时试验结果有无显著差别
## 第5步方差分析的结果显示,因素 group 对试验结果无显著影响(p = 0.149),即当 group 取不同水平时试验结果无显著差别
4 查看people和group是否存在交互效应
- 主效应:一个自变量变化时,因变量所出现的变化。
- 交互效应:反应的是两个或多个自变量对因变量的联合影响,这种影响不能简单的通过自变量的主效应相加获得。
fig, ax = plt.subplots(1,2,figsize=(12,6),dpi=600) # 1行2列的子图
sns.lineplot(y='value', x = 'people', hue = 'group', palette="tab10", data=data, ax = ax[0])
sns.lineplot(y='value', x = 'group', hue = 'people', palette="tab10", data=data, ax = ax[1])
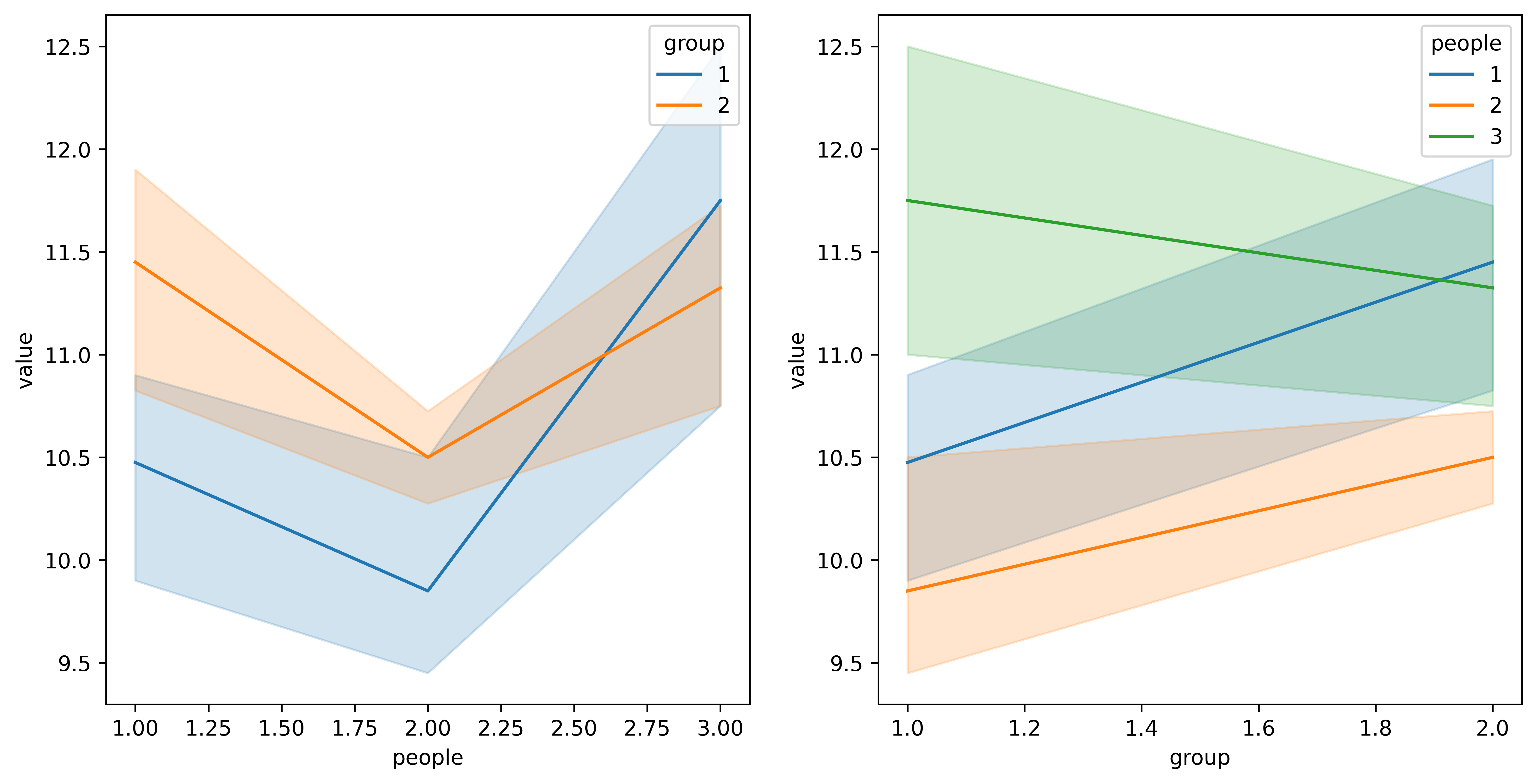
从上图可以看出,people 2和3之间是存在交互效应的,下面可以通过方差分析来检验
5 模型拟合与Two Way ANOVA:双因素方差分析
model = ols('value ~C(group) + C(people) + C(group):C(people)', data = data).fit()
anova_table = anova_lm(model, type = 2)
pd.DataFrame(anova_table)
| df | sum_sq | mean_sq | F | PR(>F) | |
|---|---|---|---|---|---|
| C(group) | 1.0 | 0.960000 | 0.960000 | 2.272189 | 0.149064 |
| C(people) | 2.0 | 7.485833 | 3.742917 | 8.858974 | 0.002096 |
| C(group):C(people) | 2.0 | 2.147500 | 1.073750 | 2.541420 | 0.106623 |
| Residual | 18.0 | 7.605000 | 0.422500 | NaN | NaN |
根据上述结果可以发现:
- people组是小于0.05的,存在显著性差异。即people因素对指标value有显著性影响。
- group和两者的交互效应是大于0.05的,接受假设,不存在显著性差异,不存在交互效应。
- 因为people对value存在显著性差异,我们得进行进一步的T检验,查看是那两组之间存在显著性差异。
print(model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: value R-squared: 0.582
Model: OLS Adj. R-squared: 0.466
Method: Least Squares F-statistic: 5.015
Date: Thu, 30 Nov 2023 Prob (F-statistic): 0.00473
Time: 17:55:19 Log-Likelihood: -20.264
No. Observations: 24 AIC: 52.53
Df Residuals: 18 BIC: 59.60
Df Model: 5
Covariance Type: nonrobust
================================================================================================coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------------------------
Intercept 10.4750 0.325 32.231 0.000 9.792 11.158
C(group)[T.2] 0.9750 0.460 2.121 0.048 0.009 1.941
C(people)[T.2] -0.6250 0.460 -1.360 0.191 -1.591 0.341
C(people)[T.3] 1.2750 0.460 2.774 0.013 0.309 2.241
C(group)[T.2]:C(people)[T.2] -0.3250 0.650 -0.500 0.623 -1.691 1.041
C(group)[T.2]:C(people)[T.3] -1.4000 0.650 -2.154 0.045 -2.766 -0.034
==============================================================================
Omnibus: 1.196 Durbin-Watson: 2.279
Prob(Omnibus): 0.550 Jarque-Bera (JB): 1.081
Skew: -0.461 Prob(JB): 0.582
Kurtosis: 2.518 Cond. No. 9.77
==============================================================================Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
print(model.params)
# 拟合公式
# Yij = 10.475*G(1)*P(1) + 0.9150*G(2) - 0.625*P(2) + 1.275*P(3) - 0.325*G(2)*P(2) -1.4*G(2)*P(3)
Intercept 10.475
C(group)[T.2] 0.975
C(people)[T.2] -0.625
C(people)[T.3] 1.275
C(group)[T.2]:C(people)[T.2] -0.325
C(group)[T.2]:C(people)[T.3] -1.400
dtype: float64
曲线拟合出来的实为每一种组合的均值:拟合参数验算
*** 无论是普通线性模型还是广义线性模型,预测的都是自变量x取特定值时因变量y的平均值。
因变量y的实际取值与其平均值之差被称为误差项,而误差的分布很大程度上决定了使用什么模型。
# Yij = 10.475*G(1)*P(1) + 0.9150*G(2) - 0.625*P(2) + 1.275*P(3) - 0.325*G(2)*P(2) -1.4*G(2)*P(3)
# GPxx:实际值
# Y_GPxx:预测值
''' Group = 1,People = 1 这个作为截距,后面的每一种组合要加上Intercept'''
Intercept = (11+9.6+10.8+10.5)/4 ''' Group = 1, People = 2 '''
GP12 = (9.4+9.6+9.6+10.8)/4
Y_GP12 = 10.475 - 0.625''' Group = 1, People = 3 '''
GP13 = (12.5+11.5+10.5+12.5)/4
Y_GP13 = 10.475 + 1.275''' Group = 2, People = 1 '''
GP21 = (10.5+11.5+12+11.8)/4
Y_GP21 = 10.475 + 0.9105''' Group = 2, People = 2 '''
GP22 = (10.8+10.5+10.5+10.2)/4
Y_GP22 = 10.475 + 0.9105 - 0.625 - 0.325''' Group = 2, People = 3 '''
GP23 = (10.5+11.8+11.5+11.5)/4
Y_GP23 = 10.475 + 0.9105 + 1.275 - 1.4print('Intercept:', Intercept)
print('GP12:',GP12, 'Y_GP12:',Y_GP12)
print('GP13:',GP13, 'Y_GP13:',Y_GP13)
print('GP21:',GP21, 'Y_GP21:',Y_GP21)
print('GP22:',GP22, 'Y_GP22:',Y_GP22)
print('GP23:',GP23, 'Y_GP23:',Y_GP23)
Intercept: 10.475000000000001
GP12: 9.850000000000001 Y_GP12: 9.85
GP13: 11.75 Y_GP13: 11.75
GP21: 11.45 Y_GP21: 11.3855
GP22: 10.5 Y_GP22: 10.435500000000001
GP23: 11.325 Y_GP23: 11.2605
6 多重比较,post hoc t-tests
print("people因子不同水平的比较结果:", pairwise_tukeyhsd(data['value'], data['people']))
print("###########################\n")
print("group 因子不同水平的比较结果:", pairwise_tukeyhsd(data['value'], data['group']))print("结果说明: reject=True,说明两组之间有显著性差异。")
people因子不同水平的比较结果: Multiple Comparison of Means - Tukey HSD, FWER=0.05
===================================================
group1 group2 meandiff p-adj lower upper reject
---------------------------------------------------1 2 -0.7875 0.0935 -1.6876 0.1126 False1 3 0.575 0.2635 -0.3251 1.4751 False2 3 1.3625 0.0028 0.4624 2.2626 True
---------------------------------------------------
###########################group 因子不同水平的比较结果: Multiple Comparison of Means - Tukey HSD, FWER=0.05
===================================================
group1 group2 meandiff p-adj lower upper reject
---------------------------------------------------1 2 0.4 0.2803 -0.3495 1.1495 False
---------------------------------------------------
结果说明: reject=True,说明两组之间有显著性差异。
7 计算效应量Correlation family: η2、ω2 (适用于 Correlational data)
神奇的发现:计算方式不同,但是η^2 = ω^2
# η^2 = (F_A X df_A)/(F_A X df_A +df_e)
yitaG = (2.272 * 1)/(2.272 * 1 + 18)
yitaP = (8.86 * 2)/(8.86 * 2 + 18)
yitaGP = (2.5414 * 2)/(2.5414 * 2 + 18)
print('Group的效应量', yitaG)
print('People的效应量',yitaP)
print('GroupxPeople的效应量',yitaGP)
Group的效应量 0.11207576953433307
People的效应量 0.49608062709966405
GroupxPeople的效应量 0.22019858942589288
# ω^2 = sq_A /(sq_A + sq_e)
oumigaG = 0.96/(0.96 + 7.605)
oumigaP = 7.486/(7.486 + 7.605)
oumigaGP = 2.147/(2.147 + 7.605)
print('Group的效应量', oumigaG)
print('People的效应量',oumigaP)
print('GroupxPeople的效应量',oumigaGP)
Group的效应量 0.11208406304728544
People的效应量 0.49605725266715256
GroupxPeople的效应量 0.22015996718621816
2. 双因素方差分析理论和公式
参考:https://zhuanlan.zhihu.com/p/33357167
3. 效应量分析
参考:https://zhuanlan.zhihu.com/p/137779235
有效的数独【矩阵】【中等】)
 用法)
![[原创][3]探究C#多线程开发细节-“用ConcurrentQueue<T>解决多线程的无顺序性的问题“](http://pic.xiahunao.cn/[原创][3]探究C#多线程开发细节-“用ConcurrentQueue<T>解决多线程的无顺序性的问题“)









)
)


)


