文章目录

• • 🥘6. N 字形变换
  • • 🍲题目
    • 🫕算法原理
    • 🥣代码实现
  • 🥗38. 外观数列
  • • 🍿题目
    • 🧂算法原理
    • 🧈代码实现

🥘6. N 字形变换

🍲题目

题目链接：6. N 字形变换 - 力扣（LeetCode）

将一个给定字符串 s 根据给定的行数 numRows ，以从上往下、从左到右进行 Z 字形排列。

比如输入字符串为 "PAYPALISHIRING" 行数为 3 时，排列如下：

P   A   H   N
A P L S I I G
Y   I   R

之后，你的输出需要从左往右逐行读取，产生出一个新的字符串，比如："PAHNAPLSIIGYIR"。

请你实现这个将字符串进行指定行数变换的函数：

string convert(string s, int numRows); 

示例 1：

输入：s = "PAYPALISHIRING", numRows = 3
输出："PAHNAPLSIIGYIR"

示例 2：

输入：s = "PAYPALISHIRING", numRows = 4
输出："PINALSIGYAHRPI"
解释：
P     I    N
A   L S  I G
Y A   H R
P     I

示例 3：

输入：s = "A", numRows = 1
输出："A"

提示：

• 1 <= s.length <= 1000
• s 由英文字母（小写和大写）、',' 和 '.' 组成
• 1 <= numRows <= 1000

🫕算法原理

这题题目有点绕，直接看图：

解法一：模拟

清楚题目的意思之后，这些过程我们是可以模拟出来的。

• 首先创建一个n行s.size()列的矩阵
• 然后填字符，假设字符坐标为(x,y)，从上往下，y轴不变，x填到x = n-1，然后斜着往上，(x-1,y+1)，填到y=0即可，以次循环，知道字符填完为止
• 最后遍历整个矩阵即可得出结果

但这个空间复杂度为O(len * n)，时间复杂度为也为O(len * n)

解法二：找规律+模拟

采用模拟的相关题目算法优化，一般都是找规律进行优化

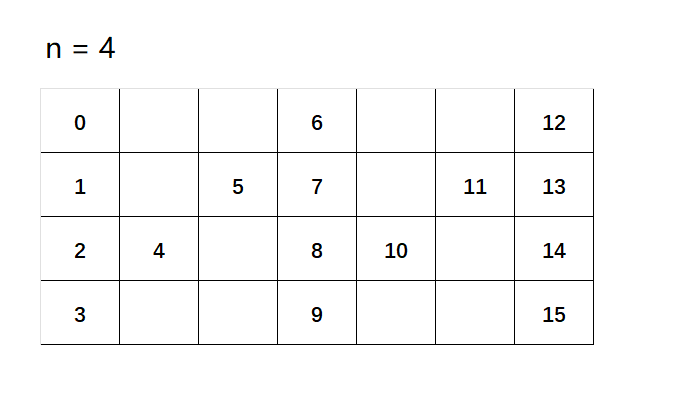
我们将字符换成对应的下标，可以发现规律：

• 第一行和最后一行的规律是一样的，它们递增是等于中间元素的个数
  即公差d = 2n -2
• 中间行的可以看作两个一起移动的，它们相加正好等于d
  即(k,d-k) -> (k+d,d-k+d)

🥣代码实现

class Solution {
public:string convert(string s, int numRows){//边界情况处理if(numRows == 1)    return s;string ans;int d = 2*numRows - 2;  //公差int n = s.size();//处理第一行for(int i = 0; i < n;i += d)ans += s[i];//处理中间行for(int k = 1; k < numRows-1; k++)  //  中间的每一行{for(int i = k, j = d-k; i < n || j < n; i += d, j += d){if(i < n)   ans += s[i];if(j < n)   ans += s[j];}}//处理最后一行for(int i = numRows-1; i < n; i+=d)ans += s[i];return ans;}
};

运行结果：

🥗38. 外观数列

🍿题目

题目链接：38. 外观数列 - 力扣（LeetCode）

给定一个正整数 n ，输出外观数列的第 n 项。

「外观数列」是一个整数序列，从数字 1 开始，序列中的每一项都是对前一项的描述。

你可以将其视作是由递归公式定义的数字字符串序列：

• countAndSay(1) = "1"
• countAndSay(n) 是对 countAndSay(n-1) 的描述，然后转换成另一个数字字符串。

前五项如下：

1.     1
2.     11
3.     21
4.     1211
5.     111221
第一项是数字 1 
描述前一项，这个数是 1 即 “ 一 个 1 ”，记作 "11"
描述前一项，这个数是 11 即 “ 二 个 1 ” ，记作 "21"
描述前一项，这个数是 21 即 “ 一 个 2 + 一 个 1 ” ，记作 "1211"
描述前一项，这个数是 1211 即 “ 一 个 1 + 一 个 2 + 二 个 1 ” ，记作 "111221"

要 描述 一个数字字符串，首先要将字符串分割为 最小 数量的组，每个组都由连续的最多 相同字符 组成。然后对于每个组，先描述字符的数量，然后描述字符，形成一个描述组。要将描述转换为数字字符串，先将每组中的字符数量用数字替换，再将所有描述组连接起来。

例如，数字字符串 "3322251" 的描述如下图：

示例 1：

输入：n = 1
输出："1"
解释：这是一个基本样例。

示例 2：

输入：n = 4
输出："1211"
解释：
countAndSay(1) = "1"
countAndSay(2) = 读 "1" = 一 个 1 = "11"
countAndSay(3) = 读 "11" = 二 个 1 = "21"
countAndSay(4) = 读 "21" = 一 个 2 + 一 个 1 = "12" + "11" = "1211"

提示：

• 1 <= n <= 30

🧂算法原理

这个题目蛮长，就是每一项都是对前一项的解释，那就是用代码来模拟这个过程，然后借用双指针left、right，让right右移，如果和s[left] == s[right]，那么right继续右移，当right停的时候，right - left就是中间相同元素的个数。

所以本次的解法就是模拟+双指针

🧈代码实现

class Solution {
public:string countAndSay(int n){string ans = "1";while(--n)  //要翻译n-1次{string tmp;int len = ans.size();for(int left = 0,right = 0; right < len; ){while(right < len && ans[left] == ans[right])   right++;tmp+=to_string(right - left) + ans[left];left = right;}ans = tmp;}  return ans;    }
};

运行结果：