实验6 回归预测实验
一、实验目的
1:了解机器学习中数据集的常用划分方法以及划分比例,并学习数据集划分后训练集、验证集及测试集的作用。
2:了解降维方法和回归模型的应用。
二、实验要求
数据集(LUCAS.SOIL_corr-实验6数据.exl)为 LUCAS 土壤数据集,每一行代表一个样本,每一列代表一个特征,特征包含近红外光谱波段数据(spc列)和土壤理化指标。
1. 对数据集进行降维处理。
2. 统计各土壤理化指标的最大值、最小值、均值、中位数,并绘制各指标的箱型图。
3. 将数据集划分后训练集、验证集及测试集。使用偏最小二乘回归法预测某一指标含量。
4. 打印训练集和验证集的R2和RMSE。
5. 绘制训练集真实标签和模型预测的标签之间的散点图。(如下图所示)
三、实验结果
1:利用PCA进行降维
在任务1中,本实验采用主成分分析(PCA)方法对数据进行降维,整体维度从1201个降低到500个。降维结束后打印数据维度的变化,如下图所示。
![]()
2:统计各个指标的数据并绘制箱型图
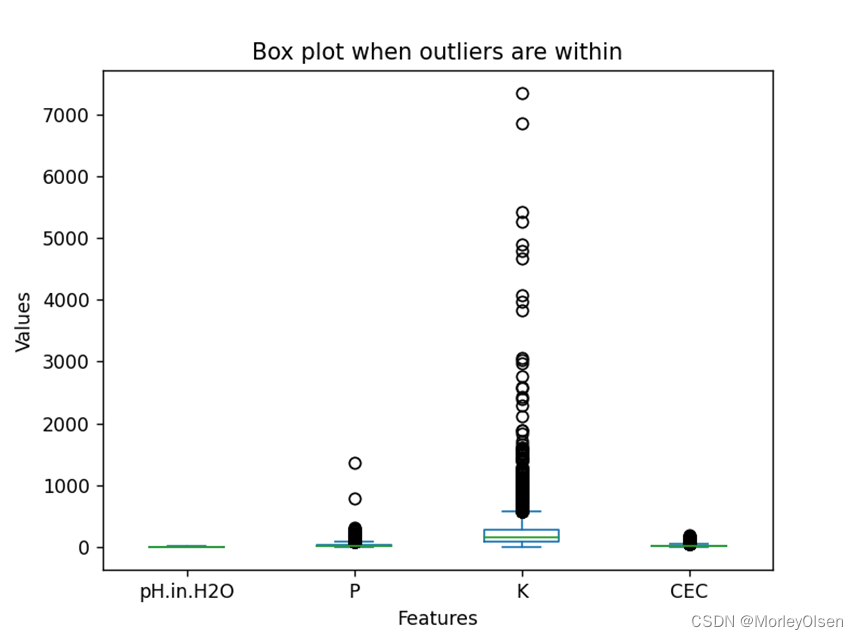
在任务2中,本实验采用agg方法对数据进行聚合操作。首先从数据中选择包含了理化指标的列名的列表,然后利用agg方法对目标列进行了多个聚合操作,最终生成了最大值、最小值、均值和中位数的结果,并保存到summary_stats这个二维数据结构之中。最终的处理结果如下图所示。

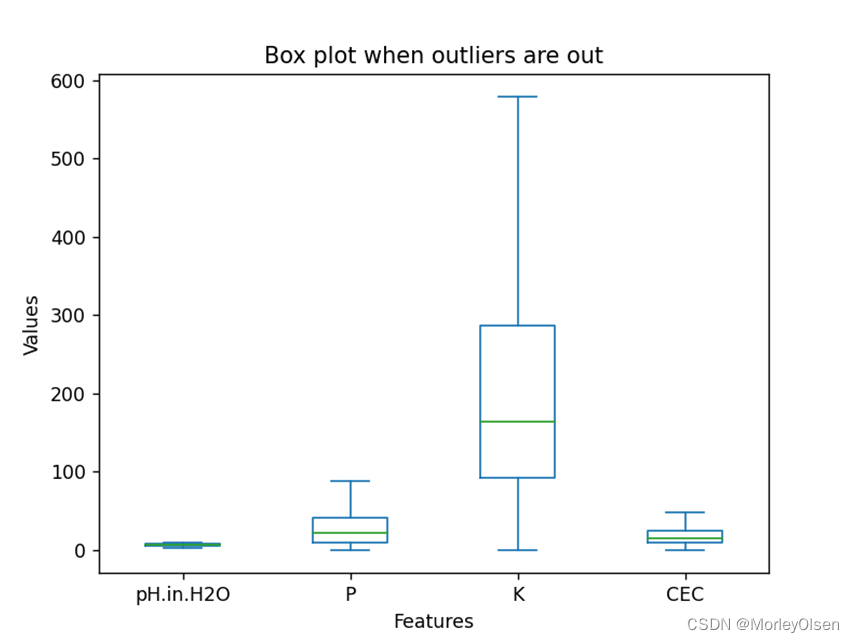
同时,本实验采用plot方法,分别生成了离群点未剔除和剔除后的箱型图。两种情况的最终结果如下图所示,图1为离群点未剔除,图2为离群点剔除。
3:划分数据集,使用偏最小二乘回归法预测pH.in.H2O指标含量
在任务3中,本实验以8:1:1的比例,将数据集随机划分成为训练集、验证集及测试集。
此外,本实验调用机器学习库中的偏最小二乘回归法,通过训练X_train和y_train来预测验证集和测试集的pH.in.H2O指标含量结果。整体代码如下图所示。

4:打印训练集和验证集的R2 和 RMSE
在任务4中,本实验调用机器学习库中的mean_squared_error函数和r2_score函数来计算验证集和测试集上的均方根误差结果和R2结果。整体代码和计算结果如下图所示,图1为调用机器学习依赖的代码,图2为验证集和测试集的均方根误差结果和R2结果。


5:绘制真实标签和模型预测的标签间的散点图。
在任务5中,本实验汇总了模型在训练集、验证集、测试集上的整体表现结果,并进行了绘图展示。最终结果如下图所示,其中蓝色的数据点表示数据来自训练集,橙色的数据点表示数据来自验证集,绿色的数据点表示数据来自测试集,红色的y=x直线为预测结果与真实值相等的标准直线。

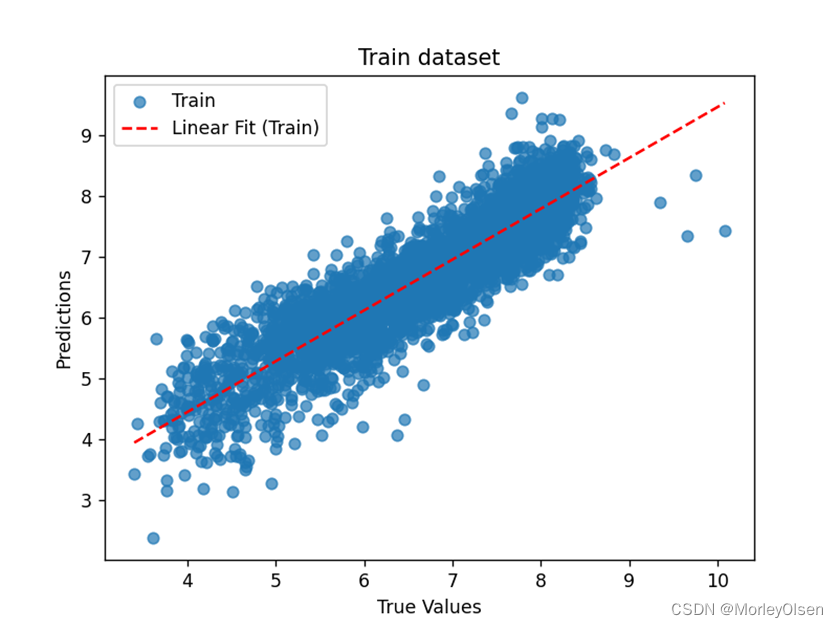
同时,本实验也分别对训练集、验证集、测试集散点图进行了散点图绘制和线性回归模型拟合。最终结果如下图所示,图1为训练集结果,图2为验证集结果,图3为测试集结果,其中红色的直线为使用线性回归模型拟合的回归线。


四、遇到的问题和解决方案
问题1:一开始设置的主成分个数过小(n_components=10),验证集和测试集的R2结果只能达到0.5左右,实验得到的相关性不够好。

解决1:增大主成分个数,并发现当n_components过百后结果较好,此时验证集和测试集的R2结果可以达到0.7+。
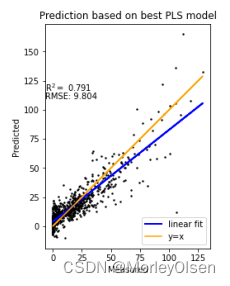
问题2:一开始进行特征列选择的时候全选了excel表格的所有列,导致模型直接以因变量进行拟合,验证集和测试集的R2高达0.99。结果如下图所示。

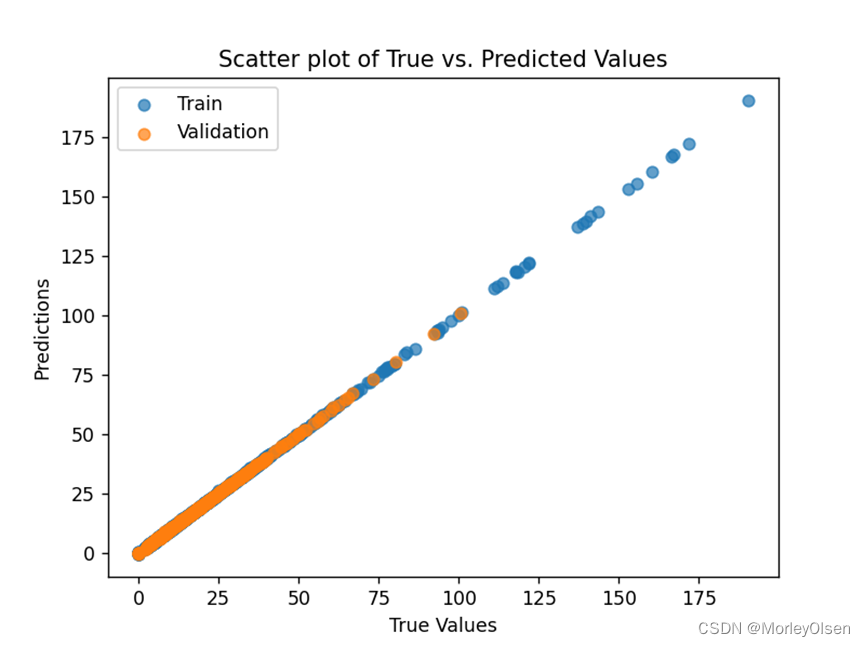
解决2:上述结果显然不符合箱型图的离散点情况。在经过一定分析之后,得知需要在选择需要进行PCA降维的特征列中,排除最后4列理化指标。即把代码更改为【selected_columns = data.columns[:-4].tolist()】。
五、实验总结和心得
1:在计算模型评价机制的时候,mean_squared_error函数中的squared参数用于控制均方误差(MSE)的计算方式。当squared=True时,它表示计算的是均方误差的平方值,即MSE。而当squared=False时,它表示计算的是均方根误差(RMSE),即MSE的平方根。
2:在划分数据集的时候,设置random_state参数可以确保数据集分割的随机性可复现。即多次运行代码时,相同的random_state值会产生相同的随机划分结果。
3:在绘制箱型图的时候,showfliers 参数用于控制箱线图中是否显示离群点(outliers)。如果将 showfliers 设置为 True,则箱线图将显示离群点,如果设置为 False,则离群点将被隐藏,只显示箱体和须部分。
4:linear fit指的是使用线性回归模型对数据进行拟合,即假设目标变量与特征之间存在线性关系。线性回归模型试图找到一条直线(或在多维情况下是一个超平面),以最佳方式拟合数据点,使得观测到的数据点与模型预测的值之间的残差平方和最小化。
5:在本实验中,我们首先对土壤理化指标进行了统计分析,包括计算最大值、最小值、均值和中位数,这有助于了解指标的分布情况和基本统计特性。同时,通过绘制每个指标的箱型图,我们可以直观地感受数据的分布和可能的离群点。
6:在本实验中,如果使用python文件运行,则每次需要较长时间等read_excel完成读入工作。后续思考后发现,可以使用jupyter notebook的ipynb文件运行,这样的话只需要读入一次数据到cell里面,后续就可以不需要重复读入了,实验效率会快很多。
六、程序源代码
各部分的任务操作在多行代码注释下构造。各段代码含有概念注释模块。
| import pandas as pd from sklearn.decomposition import PCA from sklearn.preprocessing import StandardScaler import matplotlib.pyplot as plt import numpy as np from sklearn.model_selection import train_test_split from sklearn.cross_decomposition import PLSRegression from sklearn.metrics import mean_squared_error, r2_score # 读取数据集 data = pd.read_excel(r"C:\Users\86158\Desktop\LUCAS.SOIL_corr-实验6数据.xlsx") """ 任务2:统计各土壤理化指标的最大值、最小值、均值、中位数,并绘制各指标的箱型图。 """ # 获取理化指标的列(数据最后4列) physical_chemical_columns = data.columns[-4:] new_selected = data[physical_chemical_columns] # 统计各理化指标的最大值max、最小值min、均值mean、中位数median summary_stats = data[physical_chemical_columns].agg(['max', 'min', 'mean', 'median']) print("各土壤理化指标的统计信息:") print(summary_stats) # 离群点剔除前的箱型图 boxplot1 = new_selected.plot(kind='box',showfliers=True) plt.title("Box plot when outliers are within") plt.xlabel("Features") plt.ylabel("Values") plt.show() # 离群点剔除后的箱型图 boxplot2 = new_selected.plot(kind='box',showfliers=False) plt.title("Box plot when outliers are out") plt.xlabel("Features") plt.ylabel("Values") plt.show() """ 任务1:对数据集进行降维处理。 """ # 选择需要进行PCA降维的特征列 selected_columns = data.columns[:-4].tolist() # 替换为实际的特征列名称 print("降维前的特征:",selected_columns) # 数据标准化 scaler = StandardScaler() X_scaled = scaler.fit_transform(data[selected_columns]) # 输出降维前的维度 print("降维前数据的维度:", X_scaled.shape) # 使用PCA进行降维 pca = PCA(n_components=500) # 假设降维到10个主成分,根据需要调整 X_reduced = pca.fit_transform(X_scaled) # 输出降维后的维度 print("降维后数据的维度:", X_reduced.shape) """ 任务3:将数据集划分后训练集、验证集及测试集。使用偏最小二乘回归法预测某一指标含量。 """ # 选择要预测的指标列 target_column = -4 # 选择最后一列 X = X_reduced y = data.iloc[:, target_column] # 划分数据集为训练集、验证集和测试集(比例为8:1:1) X_train, X_temp, y_train, y_temp = train_test_split(X, y, test_size=0.2, random_state=42) X_val, X_test, y_val, y_test = train_test_split(X_temp, y_temp, test_size=0.5, random_state=42) # 调用最小二乘法,使用的主成分为10个 pls = PLSRegression(n_components=500) pls.fit(X_train, y_train) # 预测验证集和测试集 y_val_pred = pls.predict(X_val) y_test_pred = pls.predict(X_test) """ 任务4:打印训练集和验证集的R2 和 RMSE。 """ # 评估性能 val_rmse = mean_squared_error(y_val, y_val_pred, squared=False) test_rmse = mean_squared_error(y_test, y_test_pred, squared=False) val_r2 = r2_score(y_val, y_val_pred) test_r2 = r2_score(y_test, y_test_pred) print(f"验证集均方根误差 (RMSE): {val_rmse}") print(f"测试集均方根误差 (RMSE): {test_rmse}") print(f"验证集R^2: {val_r2}") print(f"测试集R^2: {test_r2}") """ 任务5:绘制训练集真实标签和模型预测的标签之间的散点图。 """ y_train_pred = pls.predict(X_train) # 计算训练集、验证集、测试集的线性拟合 train_slope, train_intercept = np.polyfit(y_train, y_train_pred, 1) val_slope, val_intercept = np.polyfit(y_val, y_val_pred, 1) test_slope, test_intercept = np.polyfit(y_test, y_test_pred, 1) # 辅助线的画线范围 min_val = min(min(y_train), min(y_val), min(y_test)) max_val = max(max(y_train), max(y_val), min(y_test)) x_range = [min_val, max_val] # 训练集、验证集、测试集散点图(alpha控制透明度) plt.scatter(y_train, y_train_pred, label='Train', alpha=0.7) # plt.plot(x_range, train_slope * np.array(x_range) + train_intercept, color='blue', linestyle='--', label='Linear Fit (Train)') plt.scatter(y_val, y_val_pred, label='Validation', alpha=0.7) # plt.plot(x_range, val_slope * np.array(x_range) + val_intercept, color='orange', linestyle='--', label='Linear Fit (Validation)') plt.scatter(y_test, y_test_pred, label='Test', alpha=0.7) # plt.plot(x_range, test_slope * np.array(x_range) + test_intercept, color='green', linestyle='--', label='Linear Fit (Test)') # 添加 y=x 的标准预测直线 plt.plot(x_range, x_range, color='red', linestyle='--', label='y=x') # 图注 plt.xlabel("True Values") plt.ylabel("Predictions") plt.legend(loc='best') plt.title("Scatter plot of True vs. Predicted Values") plt.show() # 单独画训练集 plt.scatter(y_train, y_train_pred, label='Train', alpha=0.7) plt.plot(x_range, train_slope * np.array(x_range) + train_intercept, color='red', linestyle='--', label='Linear Fit (Train)') plt.xlabel("True Values") plt.ylabel("Predictions") plt.legend(loc='best') plt.title("Train dataset") plt.show() # 单独画验证集 plt.scatter(y_val, y_val_pred, label='Validation', alpha=0.7) plt.plot(x_range, val_slope * np.array(x_range) + val_intercept, color='red', linestyle='--', label='Linear Fit (Validation)') plt.xlabel("True Values") plt.ylabel("Predictions") plt.legend(loc='best') plt.title("Validation dataset") plt.show() # 单独画测试集 plt.scatter(y_test, y_test_pred, label='Test', alpha=0.7) plt.plot(x_range, test_slope * np.array(x_range) + test_intercept, color='red', linestyle='--', label='Linear Fit (Test)') plt.xlabel("True Values") plt.ylabel("Predictions") plt.legend(loc='best') plt.title("Test dataset") plt.show() |
![[Oracle]编写程序,键盘输入n,计算1+前n项之和。测试案例:输入:10 输出:22.47](http://pic.xiahunao.cn/[Oracle]编写程序,键盘输入n,计算1+前n项之和。测试案例:输入:10 输出:22.47)

——请求映射)












![[ Vue3 ] 组合式API + Setup语法糖 如何获取组件实例?](http://pic.xiahunao.cn/[ Vue3 ] 组合式API + Setup语法糖 如何获取组件实例?)



