文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法一
- 思路和算法
- 代码
- 复杂度分析
- 解法二
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:祖父结点值为偶数的结点和
出处:1315. 祖父结点值为偶数的结点和
难度
5 级
题目描述
要求
给定二叉树的根结点 root \texttt{root} root,返回祖父结点值为偶数的结点值之和。如果不存在祖父结点值为偶数的结点,返回 0 \texttt{0} 0。
一个结点的祖父结点是指该结点的父结点的父结点(如果存在)。
示例
示例 1:
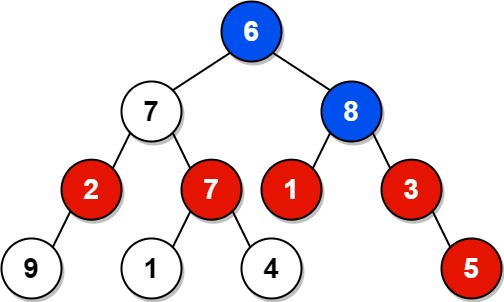
输入: root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5] \texttt{root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5]} root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5]
输出: 18 \texttt{18} 18
解释:图中红色结点的祖父结点值为偶数,蓝色结点为值为偶数的祖父结点。
示例 2:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rV1Pv0SA-1644407789559)(https://assets.leetcode.com/uploads/2021/08/10/even2-tree.jpg)]
输入: root = [1] \texttt{root = [1]} root = [1]
输出: 0 \texttt{0} 0
数据范围
- 树中结点数目在范围 [1, 10 4 ] \texttt{[1, 10}^\texttt{4}\texttt{]} [1, 104] 内
- 1 ≤ Node.val ≤ 100 \texttt{1} \le \texttt{Node.val} \le \texttt{100} 1≤Node.val≤100
解法一
思路和算法
可以使用深度优先搜索寻找所有祖父结点值为偶数的结点,并计算这些结点值之和。为了定位到祖父结点,在深度优先搜索的过程中需要记录访问的结点的父结点和祖父结点。对于每个非空结点,如果其祖父结点值为偶数,则将当前结点值加到总和中。
由于深度优先搜索只能从根结点开始遍历,而根结点没有祖父结点,因此对于每个访问到的结点,需要将当前结点作为祖父结点,寻找孙结点。当前结点的每个非空子结点的子结点即为当前结点的孙结点。在访问一个结点之后,继续访问该结点的子结点,直到遍历结束时即可得到祖父结点值为偶数的结点和。
代码
class Solution {int sum = 0;public int sumEvenGrandparent(TreeNode root) {TreeNode left = root.left, right = root.right;if (left != null) {dfs(root, left, left.left);dfs(root, left, left.right);}if (right != null) {dfs(root, right, right.left);dfs(root, right, right.right);}return sum;}public void dfs(TreeNode grandparent, TreeNode parent, TreeNode node) {if (node == null) {return;}if (grandparent.val % 2 == 0) {sum += node.val;}dfs(parent, node, node.left);dfs(parent, node, node.right);}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。每个结点都被访问一次。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是栈空间,取决于二叉树的高度,最坏情况下二叉树的高度是 O ( n ) O(n) O(n)。
解法二
思路和算法
也可以使用广度优先搜索计算祖父结点值为偶数的结点和。从根结点开始遍历所有的结点,对于每个结点,如果当前结点值为偶数且当前结点存在孙结点,则将孙结点值加到总和中。
代码
class Solution {public int sumEvenGrandparent(TreeNode root) {int sum = 0;Queue<TreeNode> queue = new ArrayDeque<TreeNode>();queue.offer(root);while (!queue.isEmpty()) {TreeNode node = queue.poll();TreeNode left = node.left, right = node.right;if (node.val % 2 == 0) {if (left != null) {if (left.left != null) {sum += left.left.val;}if (left.right != null) {sum += left.right.val;}}if (right != null) {if (right.left != null) {sum += right.left.val;}if (right.right != null) {sum += right.right.val;}}}if (left != null) {queue.offer(left);}if (right != null) {queue.offer(right);}}return sum;}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。每个结点都被访问一次。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是队列空间,队列内元素个数不超过 n n n。
)
![[Android]AlertDialog对话框](http://pic.xiahunao.cn/[Android]AlertDialog对话框)





准备)




——高斯最小频率键控(GMSK))


)



