题目描述
题目链接:622. 设计循环队列 - 力扣(LeetCode)

题目分析
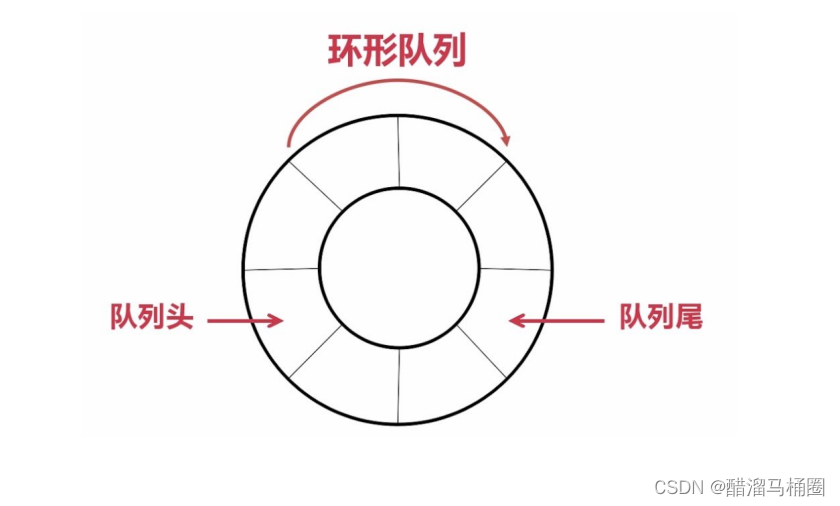
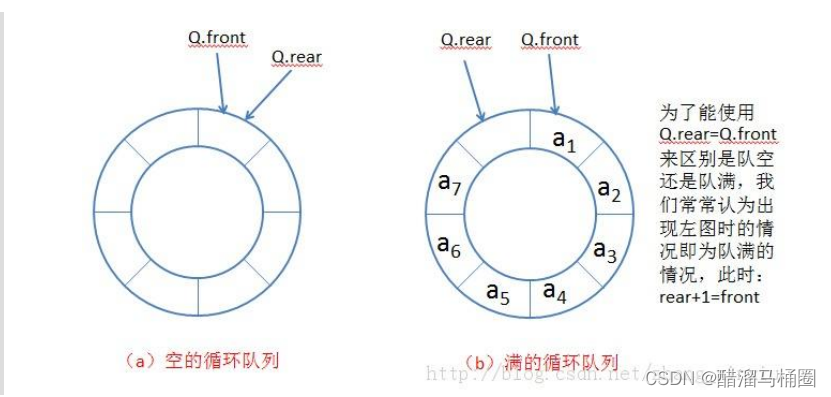
我们开辟空间的时候多开一个,k是队列的长度,我们开k+1个空间,定义一个front指向头,back的下一个指向尾
- 当front==back的时候,队列为空
- 当(back+1)%(k+)==front的时候,队列为满
这个多开的空间是移动的,出队列的时候front移动,入队列的时候back移动,当队列满的时候,(back+1)%(k+)一定==front
具体过程如下:

具体的接口有下面几个:
创建队列
用结构体封装一个数组,一个front和back,一个长度k来表示队列:
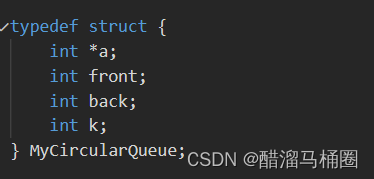
初始化
给队列开辟一块空间,给数组开辟k+1个空间,开始队列为空,front和back都为0
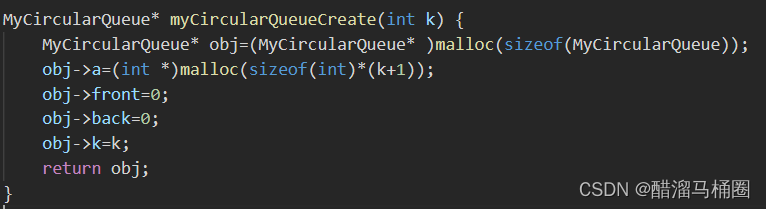
判空
front==back就为空

判满
当(back+1)%(k+)==front的时候,队列为满

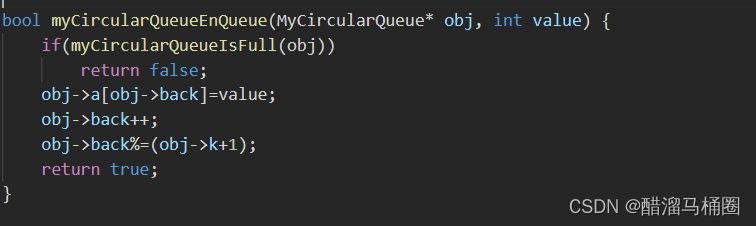
插入
如果队列满了直接返回false,如果不为满则插入到back位置,然后back++到后一个位置指向尾的下一个
当back==k+1的时候,back回到数组第一个位置,即back=back%(k+1)
一个数模一个比他大的数不会改变这个值
删除
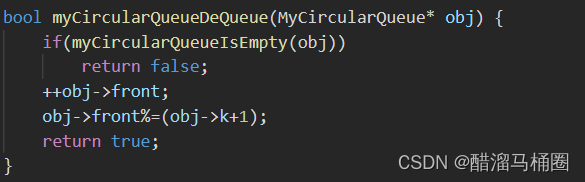
因为只有front到back之间的值是有效的,所以删除直接让front往后走就行
如果队列空了直接返回false,如果不为空则++front,返回true
同样,当front==k+1的时候,也需要回到数组第一个位置,即front=front%(k+1)
返回队头队尾的值
back指向队尾的下一个,所以返回队尾数据的时候返回的是k-1
如果back指向的是数组第一个,则返回数组的最后一个值,即a[k]
如果队列为空,则返回-1

销毁

队列的有效数据个数
现有一循环队列,其队头为front,队尾为rear(rear指向队尾数据的下一个位置),循环队列长度为N,最多存储N-1个数据,其有效长度为(rear - front + N) % N
有效长度一般是rear-front, 但是循环队列中rear有可能小于front,减完之后可能是负数,所以需要+N,此时结果刚好是队列中有效元素个数,但如果rear大于front,减完之后就是有效元素个数了,再加N后有效长度会超过N,故需要%N。
代码示例
typedef struct {int *a;int front;int back;int k;
} MyCircularQueue;MyCircularQueue* myCircularQueueCreate(int k) {MyCircularQueue* obj=(MyCircularQueue* )malloc(sizeof(MyCircularQueue));obj->a=(int *)malloc(sizeof(int)*(k+1));obj->front=0;obj->back=0;obj->k=k;return obj;
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {return obj->front==obj->back;
}bool myCircularQueueIsFull(MyCircularQueue* obj) {return (obj->back+1)%(obj->k+1)==obj->front;
}bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {if(myCircularQueueIsFull(obj))return false;obj->a[obj->back]=value;obj->back++;obj->back%=(obj->k+1);return true;
}bool myCircularQueueDeQueue(MyCircularQueue* obj) {if(myCircularQueueIsEmpty(obj))return false;++obj->front;obj->front%=(obj->k+1);return true;
}int myCircularQueueFront(MyCircularQueue* obj) {if(myCircularQueueIsEmpty(obj))return -1;return obj->a[obj->front];
}int myCircularQueueRear(MyCircularQueue* obj) {if(myCircularQueueIsEmpty(obj))return -1;if(obj->back==0)return obj->a[obj->k];elsereturn obj->a[obj->back-1];
}void myCircularQueueFree(MyCircularQueue* obj) {free(obj->a);free(obj);}/*** Your MyCircularQueue struct will be instantiated and called as such:* MyCircularQueue* obj = myCircularQueueCreate(k);* bool param_1 = myCircularQueueEnQueue(obj, value);* bool param_2 = myCircularQueueDeQueue(obj);* int param_3 = myCircularQueueFront(obj);* int param_4 = myCircularQueueRear(obj);* bool param_5 = myCircularQueueIsEmpty(obj);* bool param_6 = myCircularQueueIsFull(obj);* myCircularQueueFree(obj);
*/



)








省赛(初赛)第二场真题(原题)(题解+AC代码))


)



