目录

一、线索二叉树的基本概念

二、构造线索二叉树

三、遍历线索二叉树

---

 

---

一、线索二叉树的基本概念

遍历二叉树是以一定规则将二叉树中的结点排列成一个线性序列，得到二叉树中结点的先序序列、中序序列或后序序列。这实质上是对一个非线性结构进行线性化操作，使得每个结点（除第一个和最后一个外）在这些线性序列中有且仅有一个(直接)前序和(直接)后继。

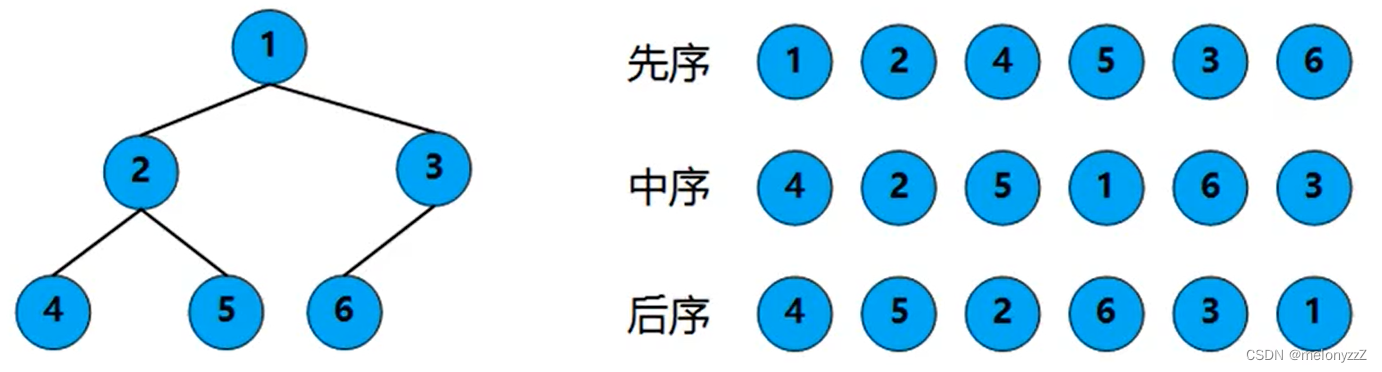
但是，当以二叉链表作为存储结构时，只能找到结点的左、右孩子信息，而不能直接得到结点在任一序列中的前驱和后继信息，这种信息只有在遍历的动态过程中才能得到，为此引入线索二叉树（Threaded Binary Tree）来保存这些动态过程中得到的有关前驱和后继的信息（线索化）。

虽然可以在每个结点中增加两个指针域来存放在遍历时得到的有关前驱和后继信息，但这样做使得结构的存储密度大大降低。由于有 n 个结点的二叉链表中必定有 n + 1 个空链域，因此可以利用这些空链域来存放结点的前驱和后继信息。

试做如下规定：

• 若结点有左子树，则左指针指向其左孩子，否则将左指针指向遍历序列中它的前驱结点。

• 若结点有右子树，则右指针指向其右孩子，否则将右指针指向遍历序列中它的后继结点。

为了避免混淆，还需改变结点结构，增加两个标志域 ltag 和 rtag。当 ltag 和 rtag 为 0 时，表示 left 和 right 指向结点的左右孩子；当 ltag 和 rtag 为 1 时，表示 left 和 right 指向结点的前驱和后继。

typedef struct ThrdBiTNode
{DataType data;struct ThrdBiTNode* left, * right;unsigned char ltag, rtag;  // 标志左右指针的类型，0 即非线索指针，1 即线索指针
}ThrdBiTNode;

---

二、构造线索二叉树

由于线索二叉树构造的实质是将二叉链表中的空指针改为指向前驱或后继的线索，而前驱或后继的信息只有在遍历时才能得到，因此线索化的过程即在遍历的过程中修改空指针的过程，可用递归算法。对二叉树按照不同的遍历次序进行线索化，可以得到不同的线索二叉树，包括先序线索二叉树、中序线索二叉树和后序线索二叉树。

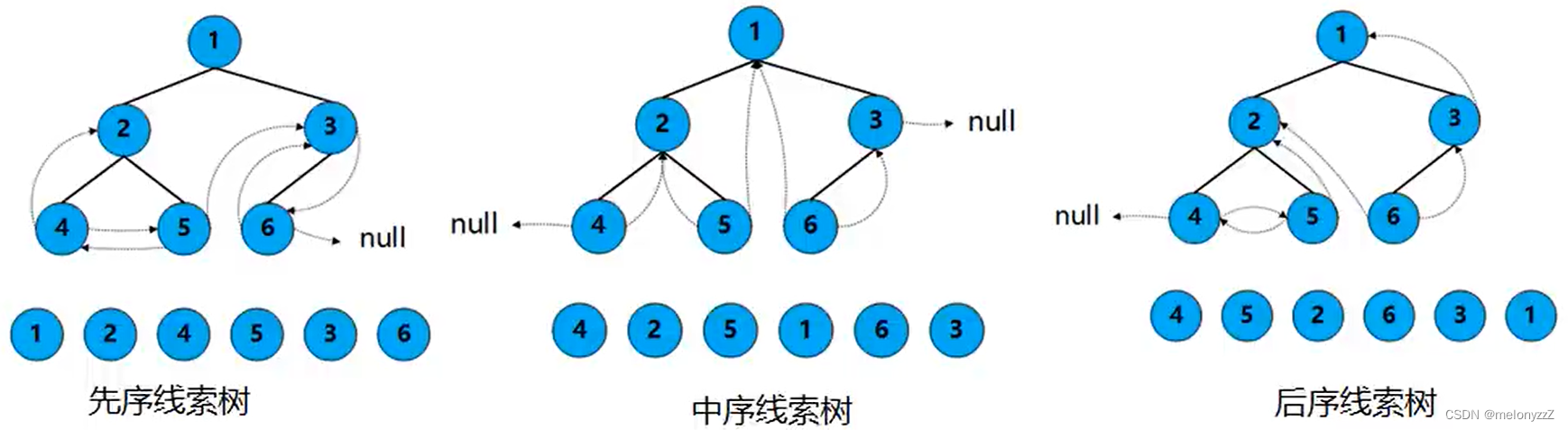
下面重点介绍中序线索化的算法。

为了记下遍历过程中访问结点的先后关系，附设一个指针 prev 始终指向刚刚访问过的结点，而指针 cur 指向当前访问的结点，由此记录下遍历过程中访问结点的先后关系。

快速创建一棵二叉树：

ThrdBiTNode* BuyThrdBiTNode(DataType x)
{ThrdBiTNode* node = (ThrdBiTNode*)malloc(sizeof(ThrdBiTNode));if (NULL == node){perror("malloc failed!");return NULL;}node->data = x;node->left = node->right = NULL;node->ltag = node->rtag = 0;return node;
}
​
// 快速创建一棵二叉树
ThrdBiTNode* CreatedBiTree()
{ThrdBiTNode* node1 = BuyThrdBiTNode(1);ThrdBiTNode* node2 = BuyThrdBiTNode(2);ThrdBiTNode* node3 = BuyThrdBiTNode(3);ThrdBiTNode* node4 = BuyThrdBiTNode(4);ThrdBiTNode* node5 = BuyThrdBiTNode(5);ThrdBiTNode* node6 = BuyThrdBiTNode(6);
​node1->left = node2;node1->right = node3;node2->left = node4;node2->right = node5;node3->left = node6;
​return node1;
}

二叉树中序线索化：

// 以结点 *cur 为根的子树中序线索化
void _InOrderThreading(ThrdBiTNode* cur, ThrdBiTNode** pprev)
{if (cur == NULL)return;
​_InOrderThreading(cur->left, pprev);  // 左子树递归线索化
​//【建立当前结点的前驱线索】// 如果当前结点的左指针为空，则将当前结点的左指针指向前驱结点if (cur->left == NULL){cur->left = *pprev;cur->ltag = 1;}//【建立前驱结点的后继线索】// 如果前驱结点的右指针为空，则将前驱结点的右指针指向当前结点if (*pprev != NULL && (*pprev)->right == NULL){(*pprev)->right = cur;(*pprev)->rtag = 1;}//【保持 prev 指向 cur 的前驱】*pprev = cur;_InOrderThreading(cur->right, pprev);  // 右子树递归线索化
}
​
// 二叉树中序线索化
void InOrderThreading(ThrdBiTNode* root)
{if (root == NULL)return;
​ThrdBiTNode* prev = NULL;_InOrderThreading(root, &prev);
​// 处理最后一个结点（最右结点）的右指针prev->right = NULL;prev->rtag = 1;
}

Test.c：

#include "ThrdBiTree.h"
​
int main()
{ThrdBiTNode* root = CreatedBiTree();InOrderThreading(root);return 0;
}

---

三、遍历线索二叉树

由于有了结点的前驱和后继信息，线索二叉树的遍历和在指定次序下查找结点的前驱和后继算法都变得简单。因此，若需经常查找结点所在遍历线性序列中的前驱和后继，则采用线索链表作为存储结构。

下面分 3 种情况讨论在线索二叉树中如何查找结点的前驱和后继。

1. 在中序线索二叉树中查找：

   (1) 查找 cur 所指结点的前驱：

   • 若 cur->ltag == 1，则结点的前驱为 cur->left 指向的结点；

   • 若 cur->ltag == 0，则说明 *cur 有左子树，结点的前驱是遍历左子树时最后访问的一个结点（即左子树中最右下的结点）。

   对中序线索二叉树进行【逆向】中序遍历：

   // 找到树中最后一个被中序遍历的结点（即最右下的结点）
   ThrdBiTNode* LastNode(ThrdBiTNode* p)
   {while (p->rtag == 0)p = p->right;return p;
   }
   ​
   // 在中序线索二叉树中找到 *cur 的前驱结点
   ThrdBiTNode* PrevNode(ThrdBiTNode* cur)
   {if (cur->ltag == 1)return cur->left;elsereturn LastNode(cur->left);
   }
   ​
   // 对中序线索二叉树进行【逆向】中序遍历
   void RevInOrder(ThrdBiTNode* root)
   {if (root == NULL){printf("\n");return;}
   ​ThrdBiTNode* cur = LastNode(root);while (cur != NULL){printf("%d ", cur->data);cur = PrevNode(cur);}printf("\n");
   }

   (2) 查找 cur 所指结点的后继：

   • 若 cur->rtag == 1，则结点的后继为 cur->right 指向的结点；

   • 若 cur->rtag == 0，则说明 *cur 有右子树，结点的后继是遍历右子树时第一个访问的结点（即右子树中最左下的结点）。

   对中序线索二叉树进行中序遍历（利用线索实现非递归算法）：

   // 找到树中第一个被中序遍历的结点（即最左下的结点）
   ThrdBiTNode* FirstNode(ThrdBiTNode* p)
   {while (p->ltag == 0)p = p->left;return p;
   }
   ​
   // 在中序线索二叉树中找到 *cur 的后继结点
   ThrdBiTNode* NextNode(ThrdBiTNode* cur)
   {if (cur->rtag == 1)return cur->right;elsereturn FirstNode(cur->right);
   }
   ​
   // 对中序线索二叉树进行中序遍历 
   void InOrder(ThrdBiTNode* root)
   {if (root == NULL){return;printf("\n");}
   ​ThrdBiTNode* cur = FirstNode(root);while (cur != NULL){printf("%d ", cur->data);cur = NextNode(cur);}printf("\n");
   }

2. 在先序线索二叉树中查找 cur 所指结点的后继：

   • 若 cur->rtag == 1，则结点后继为 cur->right 指向的结点；

   • 若 cur->rtag == 0，则说明 *cur 有右子树。按先序遍历的规则可知，*cur 的后继必为其左子树的根（若存在）或右子树的根。

3. 在后序线索二叉树中查找 cur 所指结点的前驱：

   • 若 cur->ltag == 1，则结点前驱为 cur->left 指向的结点；

   • 若 cur->ltag == 0，且 cur->rtag == 0，则说明 *cur 有右子树，此时结点后继为其右子树的根，即 cur->right 指向的结点；若 cur->rtag == 1，则说明 *cur 没有右子树，但有左子树，此时结点的后继为其左子树的根，即 cur->left 指向的结点。