线性可分SVM摘记
- 0. 线性可分
- 1. 训练样本到分类面的距离
- 2. 函数间隔和几何间隔、(硬)间隔最大化
- 3. 支持向量
\qquad 线性可分的支持向量机是一种二分类模型,支持向量机通过核技巧可以成为非线性分类器。本文主要分析了线性可分的支持向量机模型,主要取自于李航《统计学习方法》第七章。
0. 线性可分
\qquad 如下图所示,考虑训练数据“线性可分”的情况:
\qquad 
\qquad 假设分类面 w T x + b = 0 \boldsymbol w^T\boldsymbol x+b=0 wTx+b=0 可以将两类数据完整分开,任一训练样本 x \boldsymbol x x 的输出值(目标值) y y y 满足:
y = sgn ( w T x + b ) = { + 1 , w T x + b > 0 ( x ∈ ℓ 1 ) − 1 , w T x + b < 0 ( x ∈ ℓ 2 ) \qquad\qquad\qquad y=\text{sgn}(\boldsymbol w^T\boldsymbol x+b)=\begin{cases}+1,\quad\boldsymbol w^T\boldsymbol x+b>0\ (\boldsymbol x\in\ell_1)\\-1,\quad\boldsymbol w^T\boldsymbol x+b<0\ (\boldsymbol x\in\ell_2)\end{cases} y=sgn(wTx+b)={+1,wTx+b>0 (x∈ℓ1)−1,wTx+b<0 (x∈ℓ2)
\qquad
1. 训练样本到分类面的距离
\qquad 任一样本 x \boldsymbol x x 到分类面的垂直距离为: r = y ( w T x + b ) ∥ w ∥ r=\dfrac{y(\boldsymbol w^T\boldsymbol{x}+b)}{\Vert\boldsymbol w\Vert} r=∥w∥y(wTx+b)
∙ \quad\bullet ∙ 正例 x i \boldsymbol x_i xi(满足 w T x i + b > 0 , y i = + 1 \boldsymbol w^T\boldsymbol x_i+b>0,\ y_i=+1 wTxi+b>0, yi=+1)
\qquad\qquad 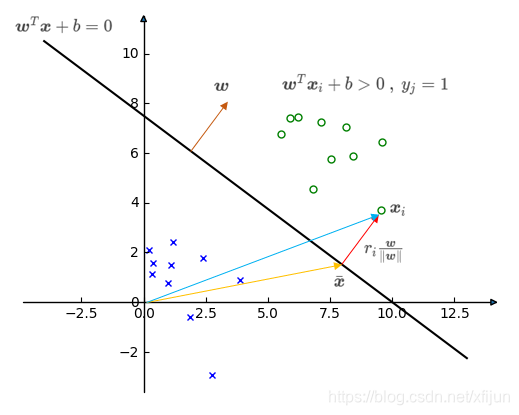
\qquad 假设 x i \boldsymbol x_i xi 到分类面的距离为 r i r_i ri,向量 x ˉ \bar{\boldsymbol x} xˉ 在分类面(满足 w T x ˉ + b = 0 \boldsymbol{w}^T\bar{\boldsymbol{x}}+b=0 wTxˉ+b=0),显然 x i = x ˉ + r i w ∥ w ∥ \boldsymbol x_i=\bar{\boldsymbol x}+r_i\dfrac{\boldsymbol w}{\Vert\boldsymbol w\Vert} xi=xˉ+ri∥w∥w
\qquad 那么
w T x i + b = w T ( x ˉ + r i w ∥ w ∥ ) + b = w T x ˉ + b + w T r i w ∥ w ∥ = r i w T w ∥ w ∥ = r i ∥ w ∥ \qquad\qquad\qquad\begin{aligned}\boldsymbol w^T\boldsymbol x_i+b&=\boldsymbol w^T(\bar{\boldsymbol x}+r_i\frac{\boldsymbol w}{\Vert\boldsymbol w\Vert})+b\\ &=\boldsymbol w^T\bar{\boldsymbol x}+b+\boldsymbol w^Tr_i\frac{\boldsymbol w}{\Vert\boldsymbol w\Vert}\\ &=r_i\frac{\boldsymbol w^T\boldsymbol w}{\Vert\boldsymbol w\Vert}\\ &=r_i\Vert\boldsymbol w\Vert\end{aligned} wTxi+b=wT(xˉ+ri∥w∥w)+b=wTxˉ+b+wTri∥w∥w=ri∥w∥wTw=ri∥w∥
\qquad 可得到正例 x i \boldsymbol x_i xi 到分类面的垂直距离 r i = w T x i + b ∥ w ∥ r_i=\dfrac{\boldsymbol w^T\boldsymbol x_i+b}{\Vert\boldsymbol w\Vert} ri=∥w∥wTxi+b
\qquad
∙ \quad\bullet ∙ 负例 x j \boldsymbol x_j xj(满足 w T x j + b < 0 , y j = − 1 \boldsymbol w^T\boldsymbol x_j+b<0,\ y_j=-1 wTxj+b<0, yj=−1)
\qquad\qquad 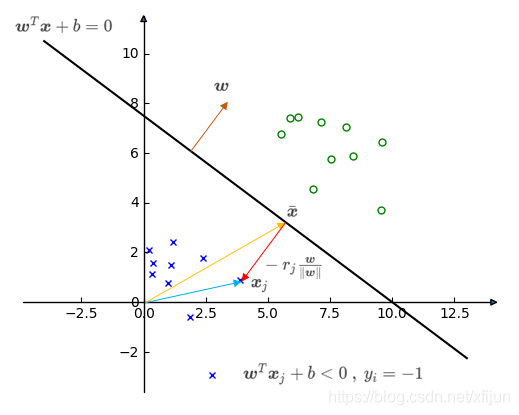
\qquad 假设 x j \boldsymbol x_j xj 到分类面的距离为 r j r_j rj,向量 x ˉ \bar{\boldsymbol x} xˉ 在分类面(满足 w T x ˉ + b = 0 \boldsymbol w^T\bar{\boldsymbol x}+b=0 wTxˉ+b=0),显然 x j = x ˉ − r j w ∥ w ∥ \boldsymbol x_j=\bar{\boldsymbol x}-r_j\dfrac{\boldsymbol w}{\Vert\boldsymbol w\Vert} xj=xˉ−rj∥w∥w
\qquad 那么
w T x j + b = w T ( x ˉ − r j w ∥ w ∥ ) + b = w T x ˉ + b − w T r j w ∥ w ∥ = − r j w T w ∥ w ∥ = − r j ∥ w ∥ \qquad\qquad\qquad\begin{aligned}\boldsymbol w^T\boldsymbol x_j+b&=\boldsymbol w^T(\bar{\boldsymbol x}-r_j\frac{\boldsymbol w}{\Vert\boldsymbol w\Vert})+b\\ &=\boldsymbol w^T\bar{\boldsymbol x}+b-\boldsymbol w^Tr_j\frac{\boldsymbol w}{\Vert\boldsymbol w\Vert}\\ &=-r_j\frac{\boldsymbol w^T\boldsymbol w}{\Vert\boldsymbol w\Vert}\\ &=-r_j\Vert\boldsymbol w\Vert\end{aligned} wTxj+b=wT(xˉ−rj∥w∥w)+b=wTxˉ+b−wTrj∥w∥w=−rj∥w∥wTw=−rj∥w∥
\qquad 可得到负例 x j \boldsymbol x_j xj 到分类面的垂直距离 r j = − w T x j + b ∥ w ∥ r_j=-\dfrac{\boldsymbol w^T\boldsymbol x_j+b}{\Vert\boldsymbol w\Vert} rj=−∥w∥wTxj+b
\qquad
2. 函数间隔和几何间隔、(硬)间隔最大化
\qquad 由于任一训练样本 x i \boldsymbol x_i xi 的输出值 y y y 满足: y = { + 1 , w T x i + b > 0 ( ∀ x i ∈ ℓ 1 ) − 1 , w T x i + b < 0 ( ∀ x i ∈ ℓ 2 ) y=\begin{cases}+1,\quad\boldsymbol w^T\boldsymbol x_i+b>0\ \ (\forall\ \boldsymbol x_i\in\ell_1)\\-1,\quad\boldsymbol w^T\boldsymbol x_i+b<0\ \ (\forall\ \boldsymbol x_i\in\ell_2)\end{cases} y={+1,wTxi+b>0 (∀ xi∈ℓ1)−1,wTxi+b<0 (∀ xi∈ℓ2),可定义两种间隔 ( margin ) (\text{margin}) (margin)来描述“训练样本 x i \boldsymbol x_i xi 到分类面的远近”。
\qquad
∙ \quad\bullet ∙ 函数间隔 ( functional margin ) (\text{functional margin}) (functional margin)
γ ^ i = y i ( w T x i + b ) = ∣ w T x i + b ∣ \qquad\qquad\hat{\gamma}_i=y_i(\boldsymbol w^T\boldsymbol x_i+b)=\vert\boldsymbol w^T\boldsymbol x_i+b\vert γ^i=yi(wTxi+b)=∣wTxi+b∣
函数间隔只能够相对地描述“训练样本 x i \boldsymbol x_i xi 到分类面的远近”。
例如, H 1 : w T x + b = 0 \mathcal H_1:\ \boldsymbol w^T\boldsymbol x+b=0 H1: wTx+b=0 与 H 2 : λ w T x + λ b = 0 \mathcal H_2:\ \lambda\boldsymbol w^T\boldsymbol x+\lambda b=0 H2: λwTx+λb=0 实际上是指同一个分类面(假设 λ > 0 \lambda>0 λ>0)
对训练样本 x i \boldsymbol x_i xi 而言,却有 { γ ^ 1 i = ∣ w T x i + b ∣ γ ^ 2 i = λ ∣ w T x i + b ∣ \begin{cases}\hat{\gamma}_{1i}=\vert\boldsymbol w^T\boldsymbol x_i+b\vert\\ \hat{\gamma}_{2i}=\lambda\vert\boldsymbol w^T\boldsymbol x_i+b\vert \end{cases} {γ^1i=∣wTxi+b∣γ^2i=λ∣wTxi+b∣,函数间隔 γ ^ 2 i = λ γ ^ 1 i \hat{\gamma}_{2i}=\lambda\hat{\gamma}_{1i} γ^2i=λγ^1i
\qquad
∙ \quad\bullet ∙ 几何间隔 ( geometricl margin ) (\text{geometricl margin}) (geometricl margin)
γ i = y i r i = y i ( w T x i + b ) ∥ w ∥ = ∣ w T x i + b ∣ ∥ w ∥ \qquad\qquad \gamma_i=y_ir_i=\dfrac{y_i(\boldsymbol w^T\boldsymbol x_i+b)}{\Vert\boldsymbol w\Vert}=\dfrac{\vert\boldsymbol w^T\boldsymbol x_i+b\vert}{\Vert\boldsymbol w\Vert} γi=yiri=∥w∥yi(wTxi+b)=∥w∥∣wTxi+b∣
几何间隔就是“训练样本 x i \boldsymbol x_i xi 到分类面的垂直距离”,也就是“规范化的函数间隔”。
上例中, { γ 1 i = γ ^ 1 i ∥ w ∥ = ∣ w T x i + b ∣ ∥ w ∥ γ 2 i = γ ^ 2 i ∥ λ w ∥ = λ ∣ w T x i + b ∣ ∥ λ w ∥ = ∣ w T x i + b ∣ ∥ w ∥ \begin{cases}\gamma_{1i}=\dfrac{\hat{\gamma}_{1i}}{\Vert\boldsymbol w\Vert}=\dfrac{\vert\boldsymbol w^T\boldsymbol x_i+b\vert}{\Vert\boldsymbol w\Vert} \\ \\\gamma_{2i}=\dfrac{\hat{\gamma}_{2i}}{\Vert\lambda\boldsymbol w\Vert}=\dfrac{\lambda\vert\boldsymbol w^T\boldsymbol x_i+b\vert}{\Vert\lambda\boldsymbol w\Vert}=\dfrac{\vert\boldsymbol w^T\boldsymbol x_i+b\vert}{\Vert\boldsymbol w\Vert} \end{cases} ⎩ ⎨ ⎧γ1i=∥w∥γ^1i=∥w∥∣wTxi+b∣γ2i=∥λw∥γ^2i=∥λw∥λ∣wTxi+b∣=∥w∥∣wTxi+b∣,几何间隔 γ 1 i = γ 2 i \gamma_{1i}=\gamma_{2i} γ1i=γ2i,仍然相等。
\qquad 显然,函数间隔和几何间隔之间的关系为:
γ = γ ^ ∥ w ∥ \qquad\qquad\textcolor{crimson}{\gamma=\dfrac{\hat{\gamma}}{\Vert\boldsymbol w\Vert}} γ=∥w∥γ^
\qquad
∙ \quad\bullet ∙ 以最大化训练样本的几何间隔为目标函数,并定义约束最优化问题
\qquad 约束最优化问题(1)
max w , b γ s . t . y i ( w T x i + b ) ∥ w ∥ ≥ γ , ∀ x i \qquad\qquad\qquad\textcolor{indigo}{\begin{aligned}&\max_{\boldsymbol w,b}\ \gamma\\ &\ s.t.\ \ \ \dfrac{y_i(\boldsymbol w^T\boldsymbol x_i+b)}{\Vert\boldsymbol w\Vert}\ge \gamma,\quad \forall\ \boldsymbol x_i\end{aligned}} w,bmax γ s.t. ∥w∥yi(wTxi+b)≥γ,∀ xi
也就是,在确保所有训练样本到分类面的垂直距离都大于 γ \gamma γ 的前提下,尽可能让(几何)间隔最大。
\qquad 利用两种间隔之间的关系 γ = γ ^ ∥ w ∥ \gamma=\dfrac{\hat{\gamma}}{\Vert\boldsymbol w\Vert} γ=∥w∥γ^,在约束最优化问题(1)中使用函数间隔 γ ^ \hat{\gamma} γ^ 来描述几何间隔 γ \gamma γ,也就是
\qquad 约束最优化问题(2)
max w , b γ ^ ∥ w ∥ s . t . y i ( w T x i + b ) ≥ γ ^ , ∀ x i \qquad\qquad\qquad\textcolor{indigo}{\begin{aligned}&\max_{\boldsymbol w,b}\ \dfrac{\hat{\gamma}}{\Vert\boldsymbol w\Vert}\\ &\ s.t.\ \ \ y_i(\boldsymbol w^T\boldsymbol x_i+b) \ge \hat{\gamma},\quad \forall\ \boldsymbol x_i\end{aligned}} w,bmax ∥w∥γ^ s.t. yi(wTxi+b)≥γ^,∀ xi
\qquad
\qquad 考虑满足约束最优化问题(2)的同一个分类面的两种表示 H 1 : ( w , b ) \mathcal H_1:(\boldsymbol w,b) H1:(w,b) 和 H 2 : ( λ w , λ b ) \mathcal H_2:(\lambda\boldsymbol w,\lambda b) H2:(λw,λb),对于任一训练样本 x i \boldsymbol x_i xi 而言( λ > 0 \lambda>0 λ>0),那么:
\qquad ① H 1 : w T x + b = 0 \quad\textcolor{firebrick}{\mathcal H_1}:\ \boldsymbol w^T\boldsymbol x+b=0 H1: wTx+b=0 (函数间隔为 γ ^ = ∣ w T x i + b ∣ \hat\gamma=\vert\boldsymbol w^T\boldsymbol x_i+b\vert γ^=∣wTxi+b∣)
⟹ { 目标函数值: γ ^ ∥ w ∥ 约束函数: y i ( w T x i + b ) ≥ γ ^ , ∀ x i \qquad\qquad\quad\Longrightarrow\quad\begin{cases}目标函数值:\quad\dfrac{\hat\gamma}{\Vert\boldsymbol w\Vert}\\ 约束函数: \quad y_i(\boldsymbol w^T\boldsymbol x_i+b) \ge \hat\gamma,\quad \forall\ \boldsymbol x_i\end{cases} ⟹⎩ ⎨ ⎧目标函数值:∥w∥γ^约束函数: yi(wTxi+b)≥γ^,∀ xi
\qquad ② H 2 : λ w T x + λ b = 0 \quad\textcolor{firebrick}{\mathcal H_2}:\ \lambda\boldsymbol w^T\boldsymbol x+\lambda b=0 H2: λwTx+λb=0 (函数间隔为 λ γ ^ \lambda\hat\gamma λγ^)
⟹ { 目标函数值: λ γ ^ ∥ λ w ∥ 约束函数: y i λ ( w T x i + b ) ≥ λ γ ^ , ∀ x i \qquad\qquad\quad\Longrightarrow\quad\begin{cases}目标函数值:\quad\dfrac{\lambda\hat\gamma}{\Vert\lambda\boldsymbol w\Vert}\\ 约束函数: \quad y_i\lambda(\boldsymbol w^T\boldsymbol x_i+b) \ge \lambda\hat\gamma,\quad \forall\ \boldsymbol x_i\end{cases} ⟹⎩ ⎨ ⎧目标函数值:∥λw∥λγ^约束函数: yiλ(wTxi+b)≥λγ^,∀ xi
\qquad
\qquad 显然,权值 ( w , b ) (\boldsymbol w,b) (w,b) 与其同比例的缩放值 ( λ w , λ b ) (\lambda\boldsymbol w,\lambda b) (λw,λb) 对于约束最优化问题(2)而言是没有影响的。
\qquad
∙ \quad\bullet ∙ 构造凸二次规划问题
\qquad 在约束最优化问题(2)中,可以简单地取函数间隔 γ ^ = 1 \hat\gamma=1 γ^=1。
假设待求解的权值为 ( w , b ) (\boldsymbol w,b) (w,b), 样本 x \boldsymbol x x 到 w T x + b = 0 \boldsymbol w^T\boldsymbol x+b=0 wTx+b=0 的几何间隔为 γ ^ ∥ w ∥ \dfrac{\hat\gamma}{\Vert\boldsymbol w\Vert} ∥w∥γ^
函数间隔 γ ^ = 1 \hat\gamma=1 γ^=1 时的几何间隔写为 1 ∥ λ ′ w ∥ \dfrac{1}{\Vert\lambda^{\prime}\boldsymbol w\Vert} ∥λ′w∥1,也就是 ( w , b ) (\boldsymbol w,b) (w,b) 缩放为了 ( λ ′ w , λ ′ b ) , λ ′ = 1 / γ (\lambda^{\prime}\boldsymbol w,\lambda^{\prime}b),\ \lambda^{\prime}=1/\gamma (λ′w,λ′b), λ′=1/γ
而 w T x + b = 0 \boldsymbol w^T\boldsymbol x+b=0 wTx+b=0 和 λ ′ w T x + λ ′ b = 0 \lambda^{\prime}\boldsymbol w^T\boldsymbol x+\lambda^{\prime}b=0 λ′wTx+λ′b=0 是同一个分类面
\qquad 那么,约束最优化问题(2)就可以写为:
max w , b γ ^ ∥ w ∥ s . t . y i ( w T x i + b ) ≥ γ ^ , ∀ x i ⟹ γ ^ = 1 max w , b 1 ∥ w ∥ s . t . y i ( w T x i + b ) ≥ 1 , ∀ x i \qquad\qquad\textcolor{darkblue}{\begin{aligned}&\max_{\boldsymbol w,b}\ \dfrac{\hat\gamma}{\Vert\boldsymbol w\Vert}\\ &\ s.t.\ \ \ y_i(\boldsymbol w^T\boldsymbol x_i+b) \ge \hat\gamma,\ \forall\ \boldsymbol x_i\end{aligned}}\quad\overset{\hat\gamma=1}\Longrightarrow\qquad\textcolor{royalblue}{\begin{aligned}&\max_{\boldsymbol w,b}\ \dfrac{1}{\Vert\boldsymbol w\Vert}\\ &\ s.t.\ \ \ y_i(\boldsymbol w^T\boldsymbol x_i+b) \ge 1,\ \forall\ \boldsymbol x_i\end{aligned}} w,bmax ∥w∥γ^ s.t. yi(wTxi+b)≥γ^, ∀ xi⟹γ^=1w,bmax ∥w∥1 s.t. yi(wTxi+b)≥1, ∀ xi
\qquad
\qquad 又由于 max 1 ∥ w ∥ ⟺ min 1 2 ∥ w ∥ 2 \max\ \dfrac{1}{\Vert\boldsymbol w\Vert}\Longleftrightarrow\min\ \dfrac{1}{2}\Vert\boldsymbol w\Vert^2 max ∥w∥1⟺min 21∥w∥2,因此可以构造出一个凸二次规划问题
\qquad 约束最优化问题(3)
min w , b 1 2 ∥ w ∥ 2 s . t . y i ( w T x i + b ) ≥ 1 , ∀ x i \qquad\qquad\qquad\textcolor{indigo}{\begin{aligned}&\min_{\boldsymbol w,b}\ \dfrac{1}{2}\Vert\boldsymbol w\Vert^2\\ &\ s.t.\ \ \ y_i(\boldsymbol w^T\boldsymbol x_i+b) \ge 1,\quad \forall\ \boldsymbol x_i\end{aligned}} w,bmin 21∥w∥2 s.t. yi(wTxi+b)≥1,∀ xi
\qquad
3. 支持向量
\qquad 支持向量 ( support vector ) (\text{support\ vector}) (support vector) 是指距离分类面最近的训练样本(红色 + 点),两个(红色点线)超平面 w T x + b = 1 \boldsymbol w^T\boldsymbol x+b=1 wTx+b=1 和 w T x + b = − 1 \boldsymbol w^T\boldsymbol x+b=-1 wTx+b=−1 之间的距离,称为间隔 ( margin ) (\text{margin}) (margin)。
\qquad 
\qquad 考察该凸二次规划最优化问题:
min w , b 1 2 ∥ w ∥ 2 s . t . y i ( w T x i + b ) ≥ 1 , ∀ x i \qquad\qquad\qquad\begin{aligned}&\min_{\boldsymbol w,b}\ \dfrac{1}{2}\Vert\boldsymbol w\Vert^2\\ &\ s.t.\ \ \ y_i(\boldsymbol w^T\boldsymbol x_i+b) \ge 1,\quad \forall\ \boldsymbol x_i\end{aligned} w,bmin 21∥w∥2 s.t. yi(wTxi+b)≥1,∀ xi
\qquad 支持向量也是使得约束条件的等式成立的点,即: y ( w T x + b ) = 1 y(\boldsymbol w^T\boldsymbol x+b)=1 y(wTx+b)=1。在线性可分的情况下,选择不同的点作为支持向量,就可以确定不同的分离超平面 w T x + b = 0 \boldsymbol w^T\boldsymbol x+b=0 wTx+b=0。
- (正例的)支持向量 x i , y i = + 1 : y i ( w T x i + b ) = 1 ⇒ H 1 : w T x i + b = 1 \boldsymbol x_i,y_i=+1:\ y_i(\boldsymbol w^T\boldsymbol x_i+b)=1 \qquad\Rightarrow\quad H_1:\boldsymbol w^T\boldsymbol x_i+b=1 xi,yi=+1: yi(wTxi+b)=1⇒H1:wTxi+b=1
其余的 (正例的)训练样本满足 w T x i + b > 1 \boldsymbol w^T\boldsymbol x_i+b>1 wTxi+b>1- (负例的)支持向量 x j , y j = − 1 : y j ( w T x j + b ) = 1 ⇒ H 2 : w T x j + b = − 1 \boldsymbol x_j,y_j=-1:y_j(\boldsymbol w^T\boldsymbol x_j+b)=1 \qquad\Rightarrow\quad H_2:\boldsymbol w^T\boldsymbol x_j+b=-1 xj,yj=−1:yj(wTxj+b)=1⇒H2:wTxj+b=−1
其余的 (负例的)训练样本满足 w T x i + b < − 1 \boldsymbol w^T\boldsymbol x_i+b<-1 wTxi+b<−1- 两个超平面 H 1 H_1 H1 与 H 2 H_2 H2 之间的间隔为 2 ∥ w ∥ \dfrac{2}{\Vert\boldsymbol w\Vert} ∥w∥2
\qquad
\qquad
【写在最后】SVM的资料太多了,越写越觉得没什么特别的内容值得去写。攒在草稿箱里太久,发出来就当留个记录吧。
)
__《Apache Tomcat 的云原生演进》)



)

![pdf文件编辑,[增删改查]](http://pic.xiahunao.cn/pdf文件编辑,[增删改查])











