机器学习中的特殊函数
- Sigmoid
- softplus函数
- tanh
- ReLu(x)
- Leaky-Relu
- ELU
- SiLu/ Swish
- Mish
- 伽玛函数
- beta函数
- Ref
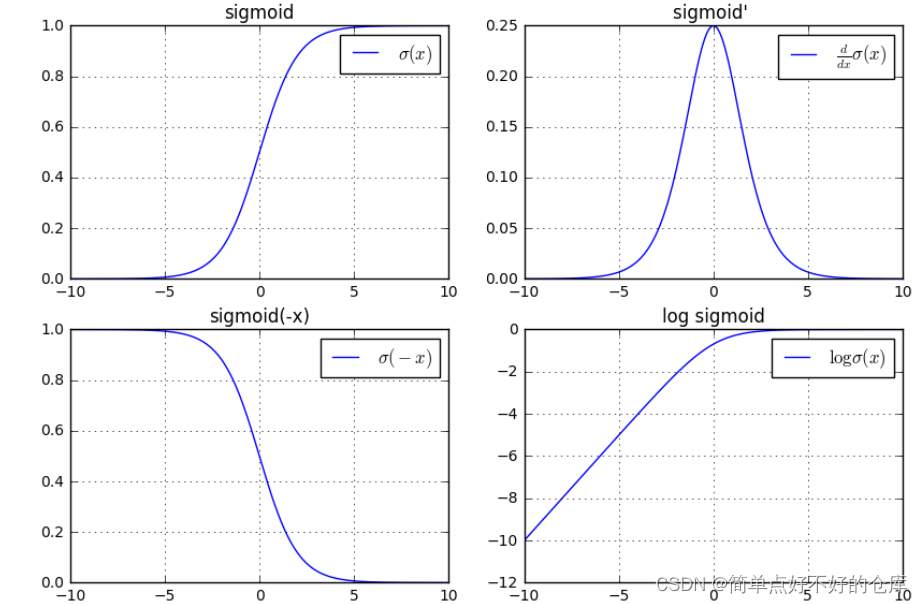
Sigmoid

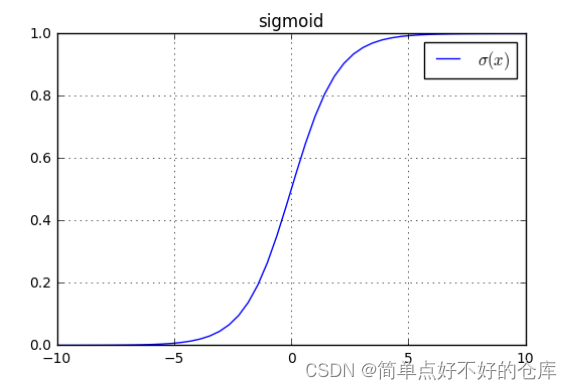
值域: 【0,1】
定义域:【负无穷,正无穷】
特殊点记忆: 经过 [0 , 0.5]
关键点[0,0.5]处的导数是 0.025
相关导数:
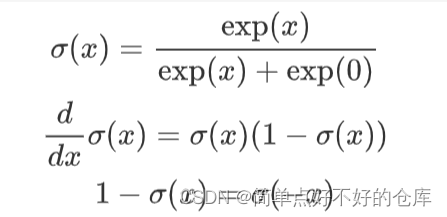
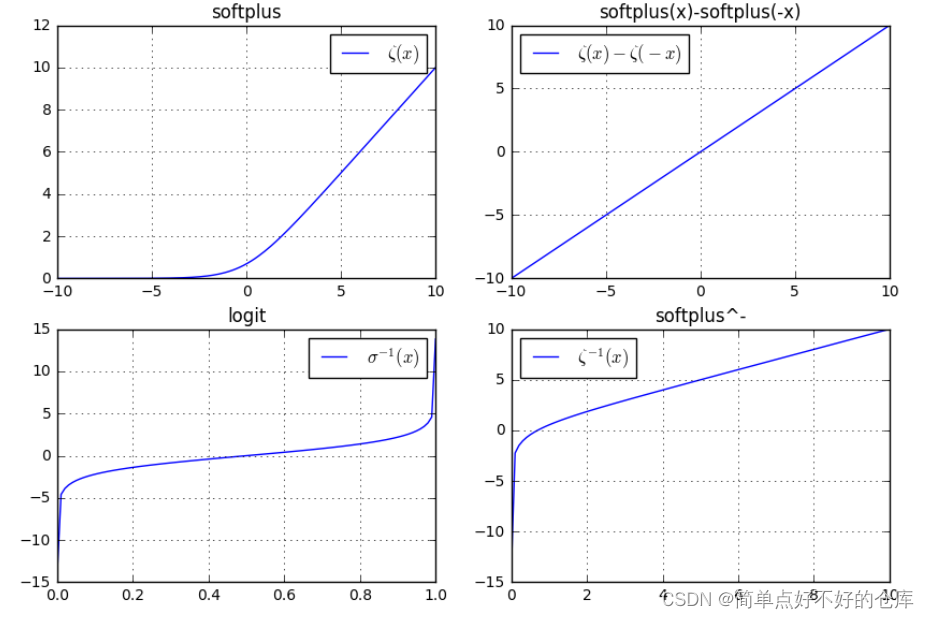
softplus函数

值域: (0,无穷大】
定义域:【负无穷,正无穷】
特殊点记忆: 经过 [0 , 1]
关键点[0,1]处的导数是 0.5,是sigmoid函数在x=0时的值
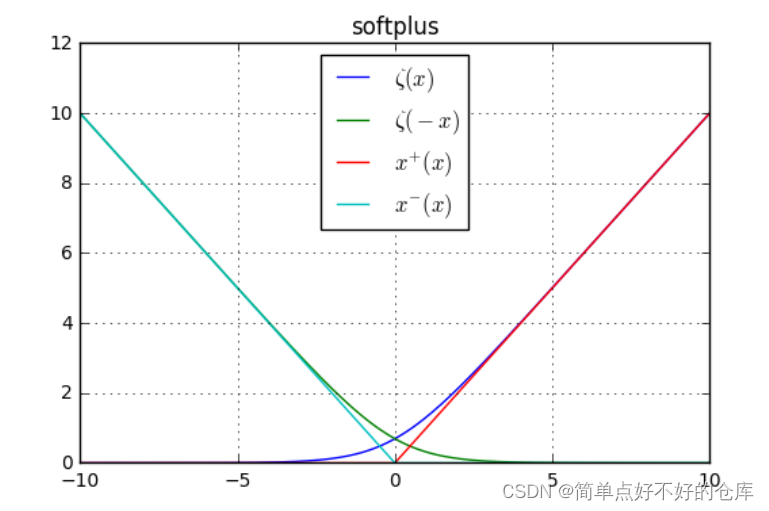
其中:
相关的导数性质:
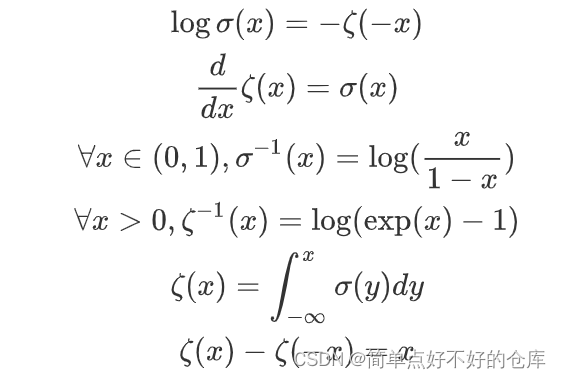
关键点[0,1]处的导数是 0.5,是sigmoid函数在x=0时的值
tanh
tanh ( x ) = e x − e − x e x + e − x \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} tanh(x)=ex+e−xex−e−x
值域: 【-1,1】
定义域:【负无穷,正无穷】
特殊点记忆: 经过 [0 , 0]
关键点[0,0]处的导数是 1

相关导数:
d d x tanh ( x ) = 1 − tanh 2 ( x ) \frac{d}{dx}\tanh(x) = 1 - \tanh^2(x) dxdtanh(x)=1−tanh2(x)
关键点[0,0]处的导数是 1
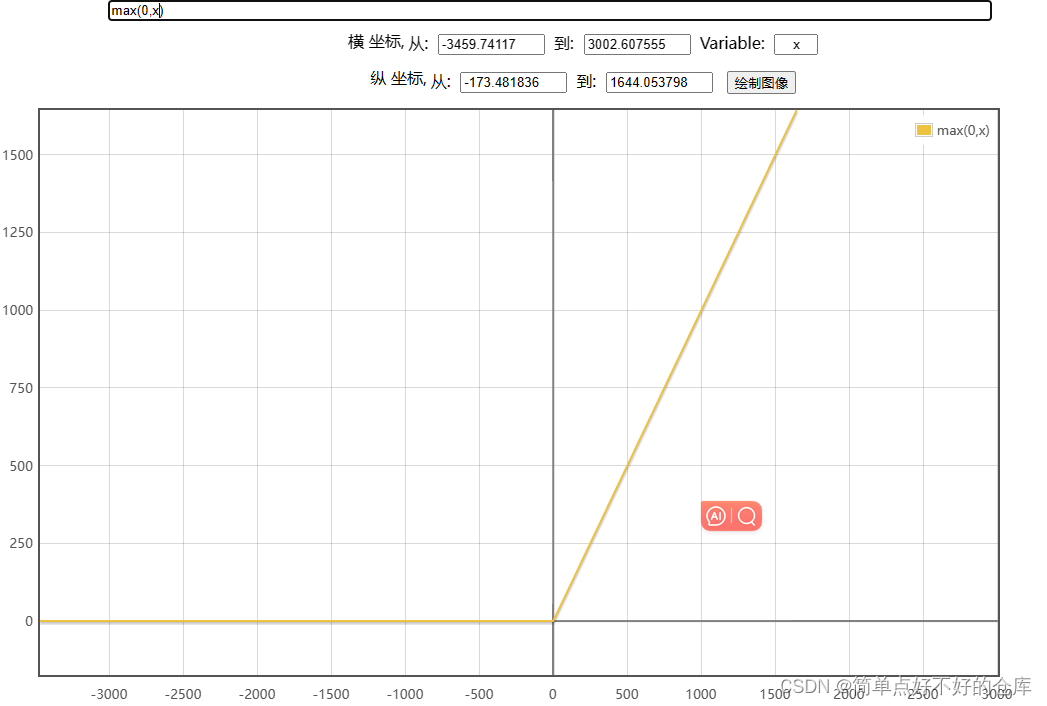
ReLu(x)
这个很简单
m a x ( 0 , x ) max(0,x) max(0,x)
Leaky-Relu
m a x ( α ∗ x , x ) max(\alpha * x, x) max(α∗x,x)
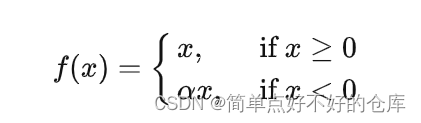
当 α = 0.1 \alpha = 0.1 α=0.1时:
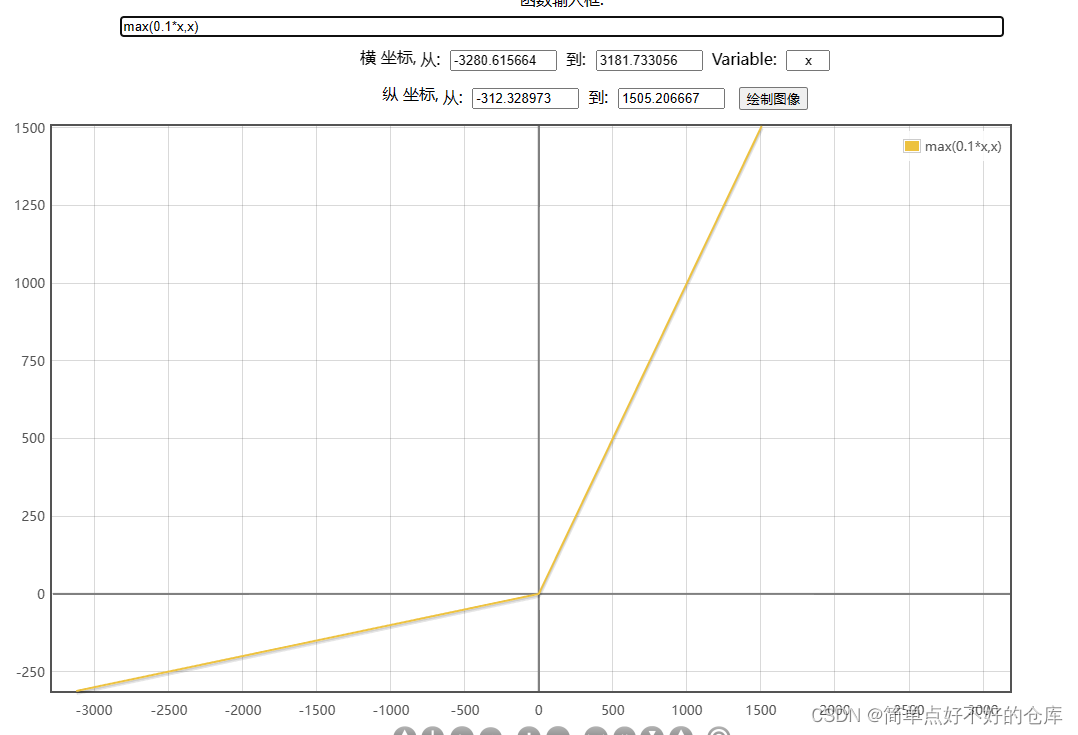
ELU

ELU是结合了sigmoid的左侧软饱和性和ReLU的右侧无饱和性而提出的一种新的激活函数。从上面图中不难看到这一特点。右侧线性部分使得ELU可以缓解梯度消失问题,而左侧软饱和性能让ELU对输入变化或噪声更鲁棒。而且ELU的输出均值接近于0,所以没有严重的偏移现象,所以收敛速度更快。但是计算复杂了些
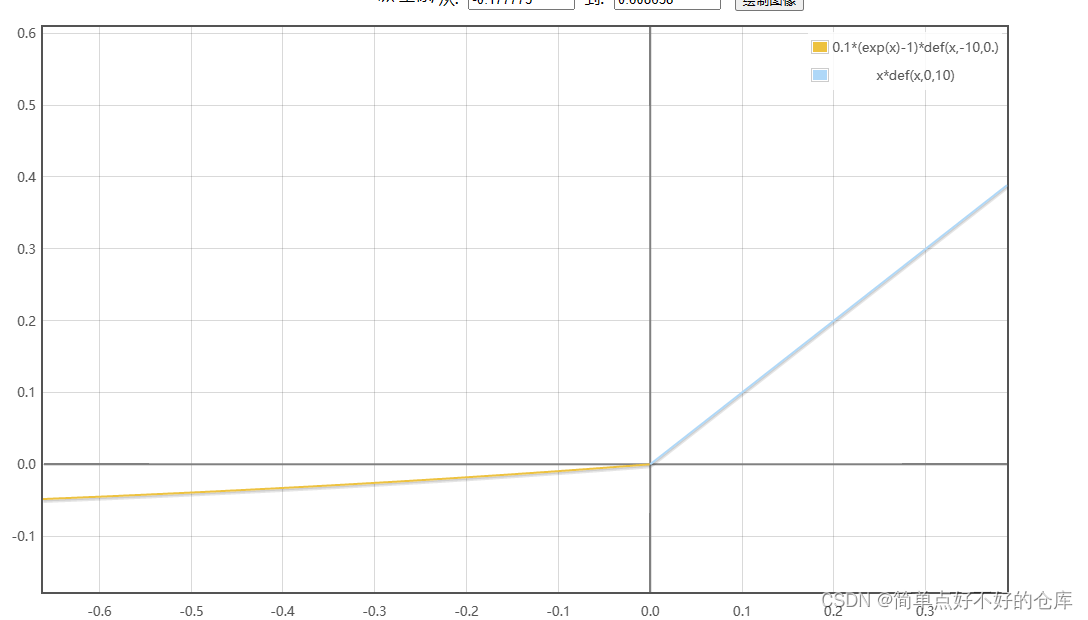
SiLu/ Swish
SiLU(Sigmoid Linear Unit)函数的 LaTeX 表达式是:
S i L U ( x ) = x ⋅ σ ( x ) SiLU(x) = x \cdot \sigma(x) SiLU(x)=x⋅σ(x)
其中, σ ( x ) \sigma(x) σ(x) 表示 sigmoid 函数,即 σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1+e^{-x}} σ(x)=1+e−x1。
SiLU 函数的值域是 ( − ∞ , ∞ ) (-\infty, \infty) (−∞,∞),因为该函数在输入值 x x x 的正负范围内都有输出。
SiLU 函数的导数表达式是:
( S i L U ( x ) ) ′ = σ ( x ) + x ⋅ σ ( x ) ⋅ ( 1 − σ ( x ) ) (SiLU(x))' = \sigma(x) + x \cdot \sigma(x) \cdot (1 - \sigma(x)) (SiLU(x))′=σ(x)+x⋅σ(x)⋅(1−σ(x))
这里的导数表达式是基于 SiLU 函数的定义和求导法则计算得出的。
需要注意的是,SiLU 函数是一种较为新型的激活函数,与传统的 sigmoid 和 ReLU 函数相比,它在某些任务上可能具有更好的性能表现。
相对于ReLU函数,SiLU函数在接近零时具有更平滑的曲线,并且由于其使用了sigmoid函数,可以使网络的输出范围在0和1之间。这使得SiLU在一些应用中比ReLU表现更好,例如在语音识别中使用SiLU比ReLU可以取得更好的效果。
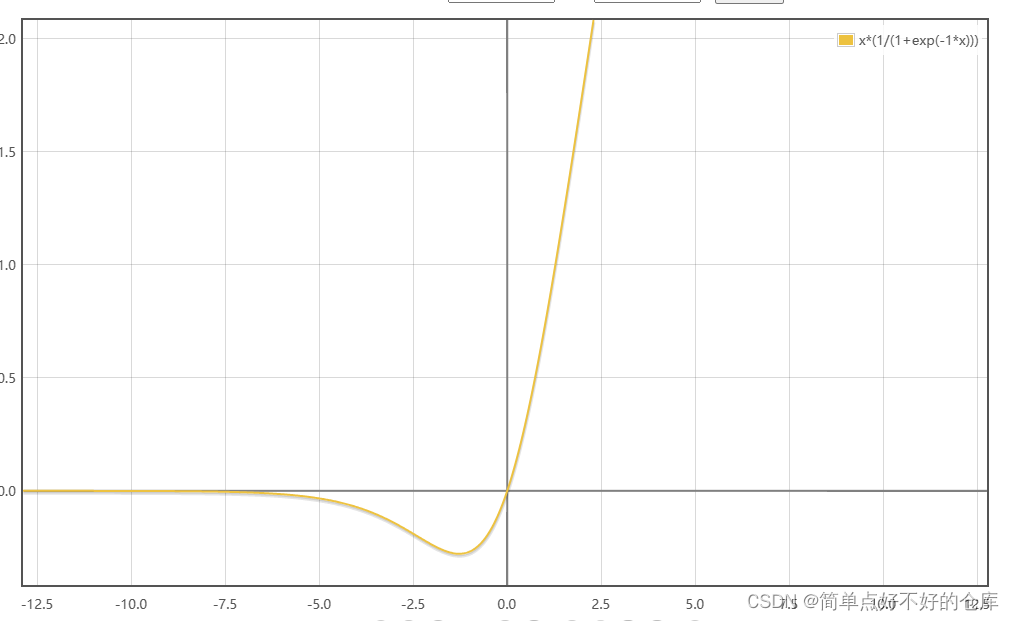
导数:
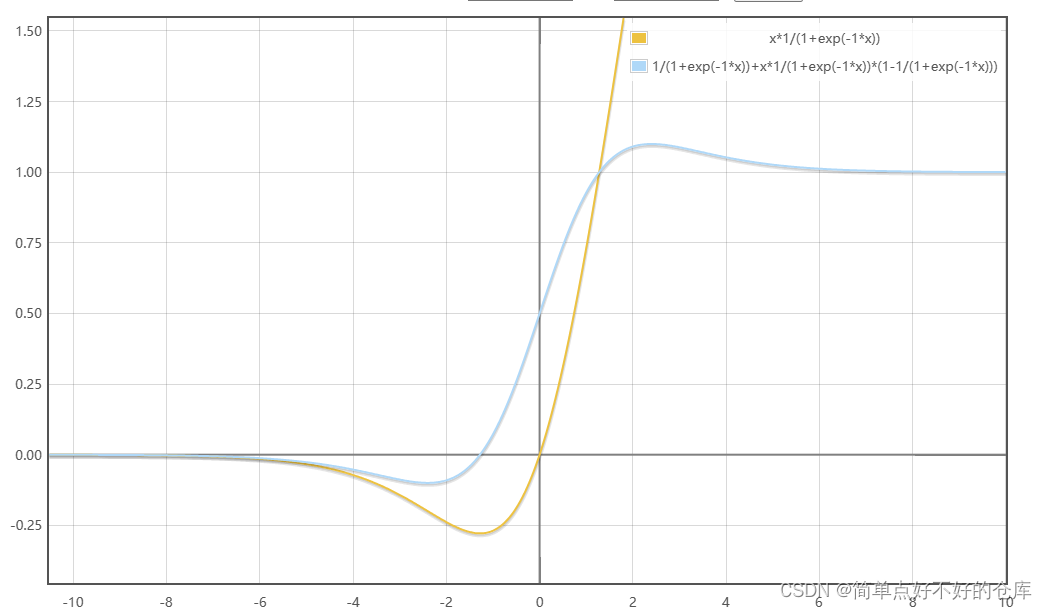
Mish
Mish激活函数的LaTeX表达式是:
M i s h ( x ) = x ⋅ tanh ( ln ( 1 + e x ) ) Mish(x) = x \cdot \tanh(\ln(1 + e^x)) Mish(x)=x⋅tanh(ln(1+ex))
Mish激活函数的值域是 ( − ∞ , ∞ ) (-\infty, \infty) (−∞,∞),与SiLU函数类似,它在输入值 x x x的正负范围内都有输出。
关于Mish激活函数的导数,其LaTeX表达式相对复杂。根据导数的定义和链式法则,我们可以推导出:
( M i s h ( x ) ) ′ = tanh ( ln ( 1 + e x ) ) + 4 e x ( 1 + e x ) 2 (Mish(x))' = \tanh(\ln(1 + e^x)) + \frac{4e^x}{(1 + e^x)^2} (Mish(x))′=tanh(ln(1+ex))+(1+ex)24ex
需要注意的是,Mish激活函数是一种相对较新的激活函数,被提出用于改善神经网络的性能。它具有一些有趣的特性,例如非单调性和自门控性质,这使得它在某些任务上可能具有更好的性能表现。与SiLU相比,Mish在一些实验中被证明能够取得更好的结果。
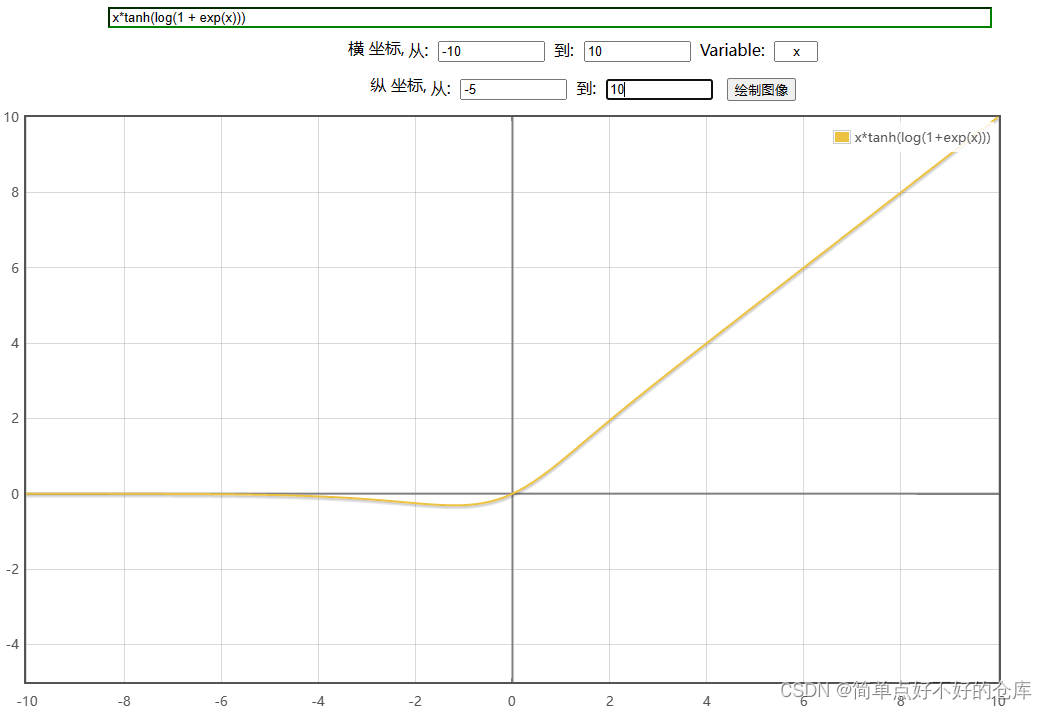
导数图:
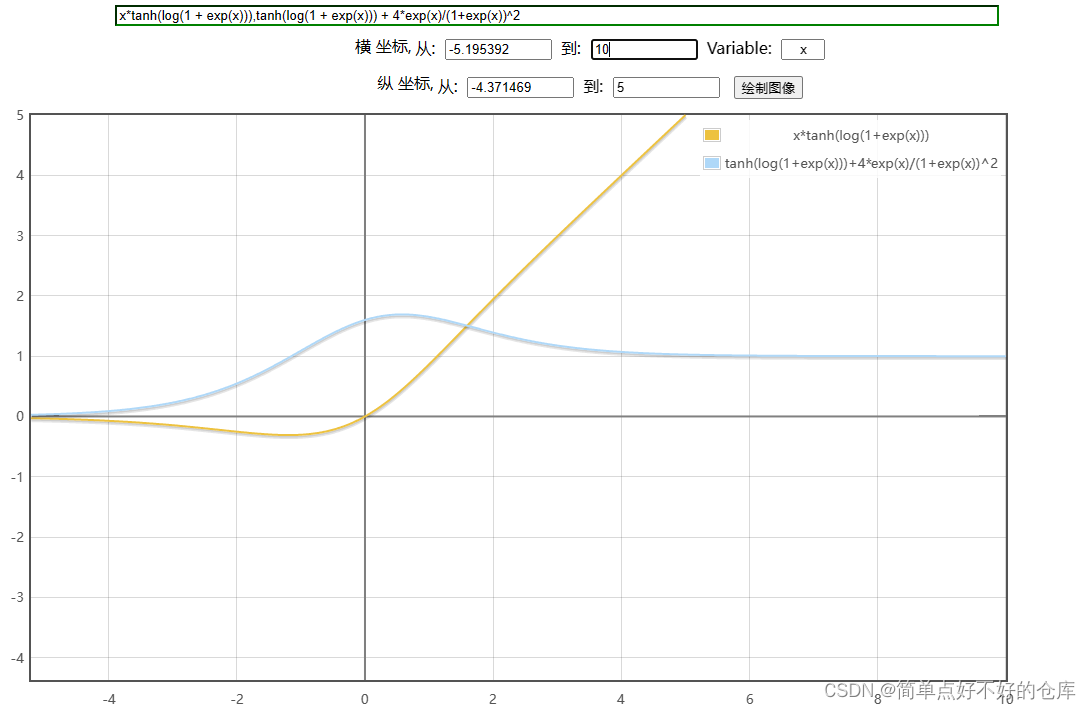
引用原始论文,Mish 是“通过系统分析和实验发现并使 Swish 更加有效”。 就目前来说Mish可能是
最好的激活函数,但请原始论文仅在计算机视觉任务上对其进行了测试。
伽玛函数
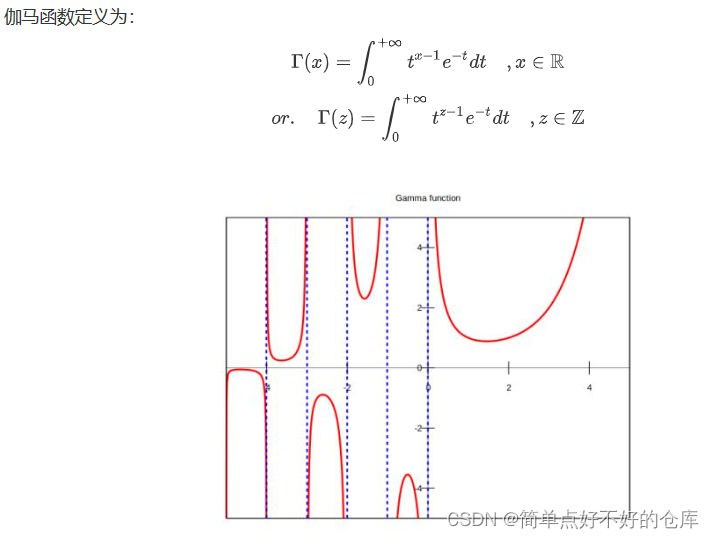


beta函数

Ref
huaxiaozhuan





,用于显示和编辑多行文本内容)








—友元、内部类、匿名对象、拷贝对象时编译器优化)





