Adversarial Attack and Defense on Graph Data: A Survey----《图数据的对抗性攻击和防御:综述》
图对抗攻击论文数据库:
https://github.com/safe-graph/graph-adversarial-learning-literature
摘要
深度神经网络(DNN)已广泛应用于各种应用,包括图像分类、文本生成、音频识别和图数据分析。然而,最近的研究表明 DNN 很容易受到对抗性攻击。尽管在图像和自然语言处理等领域有一些关于对抗性攻击和防御策略的工作,但由于其表示结构,将学到的知识直接转移到图数据仍然很困难。鉴于图分析的重要性,过去几年越来越多的研究试图分析机器学习模型在图数据上的鲁棒性。然而,考虑图数据上的对抗行为的现有研究通常侧重于具有某些假设的特定类型的攻击。此外,每项工作都提出了自己的数学公式,这使得不同方法之间的比较变得困难。因此,本次综述旨在提供 100 多篇关于图数据对抗性攻击和防御策略的论文的总体概况,并建立涵盖大多数图对抗性学习模型的统一表述。此外,我们还比较了 不同的图攻击和防御及其贡献和局限性,并总结了评估指标、数据集和未来趋势。我们希望这项调查能够帮助填补文献空白并促进这一有前景的新领域的进一步发展。
引言
近年来,深度神经网络(DNN)在多个领域取得了巨大成功,包括图像识别[55]、自然语言处理[37]、图数据应用[54]、[69]、[117]、 [118]、[138]、医疗保健分析[90]、脑回路建模[78]和基因突变功能[143]。凭借卓越的性能,深度学习已应用于自动驾驶[9]、恶意软件检测[106]、识别[107]和异常检测[42]等多项安全和安保关键任务。然而,DNN 缺乏可解释性和鲁棒性,使得它们容易受到对抗性攻击。塞格迪等人。 Szegedy 等人[111]指出了 DNN 在图像分类中的敏感性。训练有素的 DNN 的性能可能会因对抗性示例而显着降低,这些示例是精心设计的输入,并添加了少量扰动。Goodfellow等人[51]分析了这一现象,提出了一种基于梯度的方法(FGSM)来生成对抗图像样本。然后提出了不同的对抗性攻击策略来证明 DNN 在各种设置中的漏洞 [8]、[19]、[142]。例如,后来根据可转移性 [81]、[93] 和 DNN 模型 [5]、[16] 的查询反馈来探索黑盒对抗攻击。一些防御和检测方法也被用来减轻这种对抗行为[86],[102],而各种自适应攻击不断被提出,表明检测/防御通常很困难[3],[18]。
尽管对抗性攻击和防御的研究越来越多,但目前的研究主要集中在图像、自然语言和语音领域。尽管图数据在许多现实应用中很重要,但对图数据的研究还处于起步阶段。例如,在信用预测应用中,对手可以通过添加与他人的友谊关系来轻松伪装自己,这可能会造成严重后果[33]。与非图数据相比,图数据的对抗性分析提出了几个独特的挑战:1)与具有连续像素值的图像数据不同,图结构是离散值的。设计一种可以在离散空间中生成对抗性示例的有效算法是很困难的。2)对抗性扰动被设计为人类在图像域中无法察觉,因此可以强制使用特定的距离函数,例如对抗性实例和良性实例之间的 l p {l_p} lp-范数距离很小。然而,在图数据中,如何定义 “不可察觉的” 或 “微妙的扰动” 还需要进一步的分析、测量和研究。
鉴于图应用在大数据背景下的重要性以及图神经网络(GNN)的成功使用,GNN 的鲁棒性引起了学术界和工业界的极大兴趣。最近几年,人们已经做出了许多努力来探索一组 GNN 模型的对抗性攻击和防御。本文的目的是对现有的图数据对抗性学习文献进行全面的分类,开发一个框架来统一大多数现有方法,并探索未来的趋势。表3和表4列出了所有相关的攻击和防御研究,主要基于任务、策略、基线、评估指标和数据集。尽管过去三年发表了 100 多篇论文,但迄今为止仍有一些挑战尚未解决,我们在这项工作中总结和介绍如下。
全面了解。据我们所知,这项调查是首次尝试对图数据的对抗性攻击和防御的文献进行深入和全面的理解。这篇论文不仅在图神经网络(GNNs)的背景下提供了广泛的视角和关键对抗攻击与防御技术的指导,还解释了许多与 非梯度和非基于模型方法 相关的观察,并对未来的方向提供了深刻的见解。
在线更新资源。我们创建了一个开源存储库,其中包含所有相关作品,并在过去两年中对其进行了更新。该存储库包含所有相关论文和相应代码的链接,这使得研究人员更容易使用和跟踪最新进展,并可以作为该领域的基准库。然而,许多这些论文是预印本和报告,它们提供了研究结果的预览,我们将继续追踪它们并根据需要将任何更新融入存储库中。我们希望该资源能够促进对这一重要主题的进一步研究,并不断阐明未来研究和开发的各个方面。(https://github.com/safe-graph/graph-adversarial-learning-literature)
统一的问题定义。尽管图数据的攻击和防御策略多种多样,但没有统一的方法来表征它们的关系和属性;每个模型似乎都是采用独特方法的结果。有必要为易于理解现有模型和高效开发未来技术奠定良好的基础。在这篇综述中,我们率先 建立了统一的公式和定义,以系统地分析图数据上的所有对抗性攻击模型。与攻击不同,图数据的防御通常超出对抗性学习的范围,为此我们根据其独特的策略提供额外的类别。
图数据对抗分析的分类。到目前为止,有一百多篇研究图数据对抗性分析的论文。与图像数据和文本数据相比,由于图结构和任务的变化,图数据的分析更加复杂。列出所有论文可能有助于读者快速理解不同研究之间的相似点和差异,但并不直观。为此,我们总结了 基于 GNN 和 Non-GNN 方法的现有工作,旨在帮助读者轻松找到最相关的论文。我们在表 1 中展示了我们的分类法,并提供了更多详细信息。
数据集和指标。由于以往的攻击和防御工作中使用的目标和数据不同,因此很难比较不同研究的结果。目前,没有人能够直接回答“哪种攻击或防御是该领域最好的基准”这一问题。缓解这种情况的唯一方法是像其他领域一样建立一个基准[35]、[120]。为此,我们不仅根据不同标准为以前的方法开发分类法,而且还总结了经常使用的相应数据集和指标。我们希望这项研究能够为社区为该领域的未来研究和实际模型选择建立基准铺平道路。
图
在本节中,我们首先给出图数据的符号,然后介绍图类型、学习设置和应用任务的预备知识。表 2 总结了本文中最常用的符号。
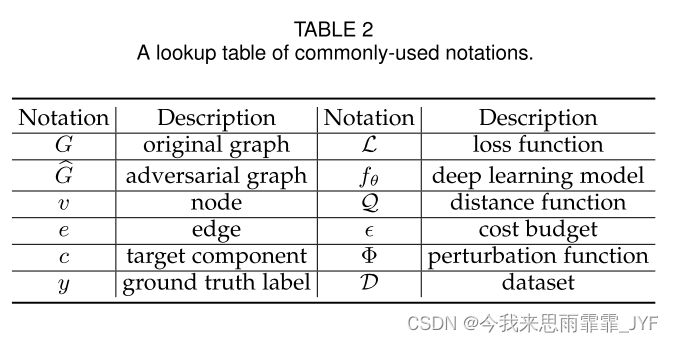
符号
我们用 G = { G i } i = 1 N G = \{ {G_i}\} _{i = 1}^N G={Gi}i=1N 来表示一组图,其中 N N N 是图的数量。每个图 G i {G_i} Gi 通常由一组节点 V i = { v j ( i ) } {V_i} = \{ v_j^{(i)}\} Vi={vj(i)} 和边 E i = { e j ( i ) } {E_i} = \{ e_j^{(i)}\} Ei={ej(i)} 表示,其中 e j ( i ) = ( v j , 1 ( i ) , v j , 2 ( i ) ) ∈ V i × V i e_j^{(i)} = (v_{j,1}^{(i)},v_{j,2}^{(i)}) \in {V_i} \times {V_i} ej(i)=(vj,1(i),vj,2(i))∈Vi×Vi 是节点 v j , 1 ( i ) v_{j,1}^{(i)} vj,1(i) 和 v j , 2 ( i ) v_{j,2}^{(i)} vj,2(i) 之间的边。节点和边都可以具有任意关联的数据,例如节点特征、边权重和边方向。根据这些属性,图数据可以分为以下不同类型。
图数据的类型
动态和静态图。从时间角度来看,图数据可以分为静态图和动态图。如果图的任何节点、边、节点特征或边特征随时间变化,则该图是动态的,表示为 G ( t ) {G^{(t)}} G(t)。相反,静态图(表示为 G G G)由一组固定的节点和边组成,不随时间变化。
静态图的一个典型例子是药物的分子结构[40]。药物一旦开发出来,其分子结构就不会随着时间而改变。社交网络[96]是动态图的一个很好的例子。由于人们经常在社交网络中添加或删除好友链接,因此关系和交互图会随着时间的推移而变化。在大多数现有的攻击工作中,研究人员研究的是对动态图的攻击。
有向图和无向图。根据起始节点和结束节点之间的方向是单向还是双向,图可以分为有向图和无向图。有向图,表示为 G ( D r ) {G^{(Dr)}} G(Dr),具有与每条边相关联的方向信息,其中任何有向边 e 1 ( i ) = ( v 1 ( i ) , v 2 ( i ) ) ≠ ( v 2 ( i ) , v 1 ( i ) ) = e 2 ( i ) e_1^{(i)} = (v_1^{(i)},v_2^{(i)}) \ne (v_2^{(i)},v_1^{(i)}) = e_2^{(i)} e1(i)=(v1(i),v2(i))=(v2(i),v1(i))=e2(i) ,而无向图的边由无序的节点对组成 e 1 ( i ) = ( v 1 ( i ) , v 2 ( i ) ) = ( v 2 ( i ) , v 1 ( i ) ) = e 2 ( i ) e_1^{(i)} = (v_1^{(i)},v_2^{(i)}) = (v_2^{(i)},v_1^{(i)}) = e_2^{(i)} e1(i)=(v1(i),v2(i))=(v2(i),v1(i))=e2(i)。
Facebook 是一个经典的无向图,A是B的朋友意味着B也是A的朋友。与友谊相反,许多真实网络(例如万维网(WWW)、食物网、神经网络、蛋白质相互作用网络和许多在线社交网络)的链接是有向或不对称加权的。Twitter 是一个典型的有向图的例子,其中有向边表示一个用户关注另一个用户的信息。
边上的属性图。边上的属性图表示为 G A e {G^{Ae}} GAe,具有与每条边相关的一些特征,表示为 x ( e j ( i ) ) ∈ R D e d g e x(e_j^{(i)}) \in {R^{{D_{edge}}}} x(ej(i))∈RDedge 。
每条边都有一个权重 x ( e j ( i ) ) ∈ R x(e_j^{(i)}) \in R x(ej(i))∈R 的加权图是边属性图的特例。交通流图[76]是加权图的典型示例,其中道路被建模为边,道路状况由边的权重表示。
节点上的属性图。节点上的属性图表示为 G ( A n ) {G^{(An)}} G(An),具有与每个节点相关的一些特征,表示为 x ( v j ( i ) ) ∈ R D n o d e x(v_j^{(i)}) \in {R^{{D_{node}}}} x(vj(i))∈RDnode 。具有不同用户的电子商务网络[43]可以被看作是一个具有节点属性的图的示例,其中每个用户被建模为节点,并具有一些特征,如人口统计信息和点击历史记录。请注意,有向图和异构信息网络是属性图的特例,广泛用于建模不同的应用程序。
图数据的学习设置
本节介绍图数据上使用的不同机器学习设置。在介绍学习设置之前,我们首先提供数学公式的符号。我们将图 G c i ∈ G {G^{{c_i}}} \in G Gci∈G 中的目标组件 c i {c_i} ci 与相应的真实标签 y i ∈ γ = { 1 , 2 , . . . , Y } {y_i} \in \gamma = \{ 1,2,...,Y\} yi∈γ={1,2,...,Y} 关联起来。这里 i ∈ [ 1 , K ] i \in [1,K] i∈[1,K], K K K 表示目标组件的总数, Y Y Y 是被预测的类的数量。数据集 D ( i n d ) = { ( c i , G c i , y i ) } i = 1 K {D^{(ind)}} = \{ ({c_i},{G^{{c_i}}},{y_i})\} _{i = 1}^K D(ind)={(ci,Gci,yi)}i=1K 由目标图组件 G c i {G^{{c_i}}} Gci、包含 c i {c_i} ci 的图以及 c i {c_i} ci 对应的真实标签表示。例如,在节点分类任务中, c i {c_i} ci 表示要分类的节点, y i {y_i} yi 表示其在 G c i {G^{{c_i}}} Gci 中的标签。根据训练和测试过程的特点,学习设置可以分为归纳学习和转导学习。
归纳学习。这是最现实的机器学习设置,其中模型通过带标签的示例进行训练,然后预测训练期间从未见过的示例的标签。在监督归纳学习设置下,分类器 f ( i n d ) ∈ F ( i n d ) : G → γ {f^{(ind)}} \in {F^{(ind)}}:G \to \gamma f(ind)∈F(ind):G→γ 被优化:
L ( i n d ) = 1 K ∑ i = 1 K L ( f θ ( i n d ) ( c i , G c i ) , y i ) {L^{(ind)}} = \frac{1}{K}\sum\limits_{i = 1}^K {L(f_\theta ^{(ind)}({c_i},{G^{{c_i}}}),{y_i})} L(ind)=K1i=1∑KL(fθ(ind)(ci,Gci),yi)
其中, L ( ⋅ , ⋅ ) L( \cdot , \cdot ) L(⋅,⋅) 默认为交叉熵, c i {{c_i}} ci 可以是其关联图 G c i {{G^{{c_i}}}} Gci 的节点、链接或子图。请注意,两个或多个不同的实例 c 1 , c 2 , . . . , c n {c_1},{c_2},...,{c_n} c1,c2,...,cn 可以与同一个图 G i ∈ G {G_i} \in G Gi∈G 相关联。
转导学习。与归纳学习不同,转导学习的测试数据是在训练过程中看到的。在这种情况下,分类器 f ( t r a ) ∈ F ( t r a ) : G → γ {f^{(tra)}} \in {F^{(tra)}}:G \to \gamma f(tra)∈F(tra):G→γ 被优化:
L ( t r a ) = 1 K ∑ i = 1 K L ( f θ ( t r a ) ( c i , G c i ) , y i ) {L^{(tra)}} = \frac{1}{K}\sum\limits_{i = 1}^K {L(f_\theta ^{(tra)}({c_i},{G^{{c_i}}}),{y_i})} L(tra)=K1i=1∑KL(fθ(tra)(ci,Gci),yi)
传导学习预测已见实例的标签,而归纳学习则预测未见实例的标签。
图数据学习的统一表述。我们给出一个统一的公式来表示监督归纳学习和转导学习,如下所示:
L ( ⋅ ) = 1 K ∑ i = 1 K L ( f θ ( ⋅ ) ( c i , G c i ) , y i ) {L^{( \cdot )}} = \frac{1}{K}\sum\limits_{i = 1}^K {L(f_\theta ^{( \cdot )}({c_i},{G^{{c_i}}}),{y_i})} L(⋅)=K1i=1∑KL(fθ(⋅)(ci,Gci),yi) (1)
在本次调查中,我们主要关注监督学习环境,同时也介绍了无监督学习环境中的一些新研究。
应用
本节我们将介绍图数据的主要任务,包括节点级、链接级和图级应用。此外,我们还介绍了如何使用方程(1)的统一公式定义下面的每个应用程序任务。
节点级应用。节点级应用是学术界和工业界最流行的一种。一个典型的例子是对 Web 和社交网络图中的节点进行标记,其中可能包含数百万个节点,例如 Facebook 和 Twitter。
大多数现有论文[10]、[11]、[33]、[121]、[139]、[146]、[174]、[176]、[178]、[179]关注节点级应用。所有这些论文都研究了转导学习环境中的节点分类,其目标函数可以通过修改方程(1)来制定。其中, f θ ( ⋅ ) = f θ ( t r a ) f_\theta ^{( \cdot )} = f_\theta ^{(tra)} fθ(⋅)=fθ(tra) ,此处 c i {{c_i}} ci 是目标节点的表示,其关联图 G c i {{G^{{c_i}}}} Gci 被设置为单个图 G G G。
现有的工作很少讨论 归纳学习 环境中的节点级应用。然而,这些应用程序经常出现在现实生活中。例如,第一方只有几个大型的公共网络信息,例如 Facebook 和 Twitter。第二方拥有私有的未标记图数据,其中可以使用来自第一方的信息来预测节点。在这种情况下,节点级分类任务不再是转导学习。通过修改方程(1)可以很容易地制定。 其中, f θ ( ⋅ ) = f θ ( i n d ) f_\theta ^{( \cdot )} = f_\theta ^{(ind)} fθ(⋅)=fθ(ind) 且此处 c i {{c_i}} ci 仍是目标节点的表示。
链接级应用。动态图上的链接预测是最常见的链接级应用之一。这些模型试图预测当前网络中缺失的链接,以及未来网络中的新链接或已解散的链接。相应的攻击和防御已在[108]、[172]中讨论。
与节点分类任务相比,链接预测任务仍然使用节点特征,但针对的是图中缺失或未标记的链接。因此,我们可以通过稍微修改等式(1)来制定链接预测任务。其中, c i {c_i} ci 表示链接目标, y i ∈ { 0 , 1 } {y_i} \in \{ 0,1\} yi∈{0,1}。
图级应用。图级任务经常出现在化学或医学领域,例如药物分子图和脑图的建模。在[33]中,整个图被用作样本实例。与此设置不同,一些其他图级应用程序使用较大图的子图来执行特定任务[141],[165]。
与现有的节点分类和链接预测方法相比,图分类采用图结构表示作为特征对无标签的图实例进行分类。因此,我们可以通过将 c i {c_i} ci 设置为图目标的表示,对式(1)稍作修改,来制定图分类任务。
图数据的对抗性攻击
在本节中,我们给出了图数据对抗性攻击的一般定义和分类,然后介绍了不可感知性指标、攻击类型、攻击任务和攻击知识水平。
统一的定义和表述
定义 3.1。(图数据的一般对抗性攻击)给定数据集 D = ( c i , G i , y i ) D = ({c_i},{G_i},{y_i}) D=(ci,Gi,yi),稍微修改 G i {G_i} Gi(记为 G ^ c i {\hat G^{{c_i}}} G^ci )后,对抗样本 G ^ c i {\hat G^{{c_i}}} G^ci 和 G i {G_i} Gi 在不可感知性指标下应该相似,但是图任务的性能变得比以前差很多。
现有文献[10]、[21]、[25]、[32]、[33]、[41]、[57]、[75]、[108]、[121]、[139]、[146]、[176]、[178]考虑图数据的对抗行为,通常侧重于假设特定类型的攻击。此外,每一项工作都提出了自己的数学公式,这使得不同方法之间的比较困难。为了帮助研究人员理解不同问题之间的关系,我们提出了一个可以涵盖所有当前现有工作的统一问题表述。
定义 3.2。(图数据的对抗性攻击:统一公式) f f f 可以是图数据上的任何学习任务函数,例如链接预测、节点级嵌入、节点级分类、图级嵌入和图级分类。 Φ ( G i ) \Phi ({G_i}) Φ(Gi) 表示原始图 G i {G_i} Gi 上的扰动空间,数据集 D ^ = { ( c i , G ^ c i , y i ) } i = 1 N \hat D = \{ ({c_i},{\hat G^{{c_i}}},{y_i})\} _{i = 1}^N D^={(ci,G^ci,yi)}i=1N 表示被攻击的实例。攻击可以描述为,
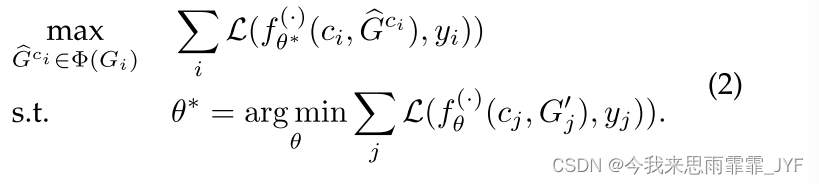
其中,当 G j ′ = G ^ c i {G'_j} = {\hat G^{{c_i}}} Gj′=G^ci 时,式(2)表示投毒攻击,而当 G j ′ {G'_j} Gj′ 为未修改的原始 G G G 时,式(2)表示逃避攻击。 f θ ( ⋅ ) = f θ ( i n d ) f_\theta ^{( \cdot )} = f_\theta ^{(ind)} fθ(⋅)=fθ(ind) 表示归纳学习, f θ ( ⋅ ) = f θ ( t r a ) f_\theta ^{( \cdot )} = f_\theta ^{(tra)} fθ(⋅)=fθ(tra) 表示转导学习。
请注意,对于 G ^ c i ∈ Φ ( G ) {\hat G^{{c_i}}} \in \Phi (G) G^ci∈Φ(G), ( c i , G ^ c i ) ({c_i},{\hat G^{{c_i}}}) (ci,G^ci) 可以表示节点操作、边操作或两者。对于任意 G ^ c i ∈ Φ ( G ) {\hat G^{{c_i}}} \in \Phi (G) G^ci∈Φ(G),要求 G ^ c i {\hat G^{{c_i}}} G^ci 与原始图 G j {G_j} Gj 相似或接近,这种相似性度量可以通过下面的通用距离函数来定义:
Q ( G ^ c i , G i ) < ε s . t . G ^ c i ∈ Φ ( G ) \begin{array}{l} Q({{\hat G}^{{c_i}}},{G_i}) < \varepsilon \\ s.t.{{\hat G}^{{c_i}}} \in \Phi (G) \end{array} Q(G^ci,Gi)<εs.t.G^ci∈Φ(G)
其中, Q ( ⋅ , ⋅ ) Q( \cdot , \cdot ) Q(⋅,⋅) 表示距离函数, ε \varepsilon ε 表示距离或成本预算的参数。
讨论:图距离函数。图距离函数可以通过多种方式定义,其中很多已经在 图隐私保护 相关工作中进行了讨论[70]。此类距离函数包括给定节点的公共邻居数、余弦相似度、杰卡德相似度等。然而,其中很少有人深入讨论对抗行为(博弈论中的对抗成本)。一般来说,攻击者的目标是对现有图进行“最小”扰动,因此这种距离测量对于衡量攻击的质量非常重要。如何设计和选择合适的距离函数来量化不同攻击场景下的攻击能力对于开发针对特定威胁模型的防御方法也至关重要。我们将在第 3.2 节中详细讨论潜在的扰动评估指标。
除了每个图距离函数的独特属性之外,分析它们之间的 “等价性” 也很有趣。例如,攻击者旨在通过添加/删除图中的一条边来攻击一个节点,可能会遇到与添加/删除边类似的“对抗成本”。不难看出,通过使用图距离函数或相似性度量,只有少数目标才是攻击者的最佳选择(具有不同的距离),因此这也有助于优化对抗目标。总之,由于图表示和对抗行为的复杂性和多样性,扰动评估或图相似性测量将取决于各种因素,例如不同的学习任务、对抗策略和对抗成本类型。
对抗性扰动
为了在图数据上生成对抗性样本,我们可以修改原始图中的节点或边。然而,修改后的图 G ^ \hat G G^ 需要基于某些扰动评估指标与原始图 G G G “相似”,并且保持“不可察觉”。以下指标有助于理解如何定义 “难以察觉的扰动”。
边级扰动。在大多数现有的工作中,攻击者能够在给定的预算内添加/删除/重新连接整个原始图中的边。在这种情况下,通常使用修改边的数量 m m m 来评估扰动的大小。除了其他扰动之外,防御者很难发现边扰动,尤其是在动态图中。
节点级扰动。攻击者还能够添加/删除节点,或操纵目标节点的特征。这种情况下的评估度量可以根据 修改的节点数量 或 良性和对抗性特征向量之间的距离 来计算。
结构保持扰动。与边级扰动类似,攻击者可以在给定预算内根据图结构修改图中的边。与一般的边级扰动相比,这考虑了更多的结构保留,例如总度、节点分布等。例如,在[176]中,攻击者需要保留图的关键结构特征,例如度分布。因此,这里的扰动可以通过图结构漂移来衡量。
属性保持扰动。在属性图中,每个节点或边都有自己的特征。除了操纵图结构之外,攻击者还可以选择修改节点或边的特征来生成图数据上的对抗性样本。基于图属性特性的各种测量可以被分析以表征扰动的幅度。例如,在参考文献[176]中,作者认为如果在共现图上的概率随机游走器可以从现有特征开始以高概率到达添加的特征,那么添加特征是不可察觉的。请注意,大多数GNN方法都学习每个节点的特征表示,这意味着它很容易受到纯结构、纯特征扰动或两者的攻击。
不可察觉的扰动评估的原则。鉴于各种图距离讨论,现有研究中尚未明确讨论如何设置图数据攻击的对抗成本。因此,我们总结了以下定义扰动评估指标的一些原则,以供将来的研究使用。
- 对于 静态图,修改边的数量以及良性和对抗性特征向量之间的距离都应该很小。
- 对于 动态图,我们可以根据随时间变化的内在信息来设置距离或对抗成本。例如,通过统计分析,我们可以得到实践中操纵的信息的上限,并利用该信息设定一个难以察觉的界限。
- 对于图数据上的各种学习任务,例如节点或图分类,我们需要使用合适的图距离函数来计算良性样本与其对抗样本之间的相似度。例如,我们可以使用公共邻居的数量来评估两个节点的相似度,但这不适用于两个单独的图。
综上所述,与图像和文本数据相比,攻击者首先可以修改信息网络上的更多特征,也可以根据图数据的格式和应用任务探索更多角度来定义“不可感知”。
攻击阶段(训练或测试阶段)
对抗性攻击可以发生在两个阶段:躲避攻击(模型测试)和中毒攻击(模型训练)。这取决于攻击者插入对抗性扰动的能力:
中毒攻击。中毒攻击试图通过将对抗性样本添加到 训练数据集中 来影响模型的性能。现有的大多数工作都是投毒攻击,它们的节点分类任务是在转导学习设置中执行的。在这种情况下,一旦攻击者更改了数据,模型就会重新训练。
躲避攻击。躲避攻击是指假设 训练好 的模型的参数是固定的。攻击者尝试生成训练模型的对抗样本。躲避攻击仅改变测试数据,不需要重新训练模型。
攻击对象
尽管所有对抗性攻击都在修改数据,但攻击者需要选择其攻击目标:模型或数据。在这种情况下,我们可以将它们概括为模型目标和数据目标。
模型目标。模型目标是使用各种方法攻击特定模型。可能是躲避攻击,也可能是中毒攻击。当前大多数对抗性攻击都与模型目标攻击有关。目标可以是 GNN 或其他学习模型。攻击者希望被攻击模型在多种情况下变得不起作用。模型目标攻击可以根据是否使用模型的 梯度信息 来分类。
- 基于梯度的攻击。在大多数研究中,我们可以看到基于梯度的攻击始终是最简单、最有效的方法。大多数基于梯度的攻击,无论是白盒还是黑盒,都会尝试获取或估计梯度信息以找到对模型最重要的特征。基于上述知识,攻击者可以根据特征对模型的重要性来选择修改有限的信息,并在使用修改后的信息时使模型不准确[10],[33],[176]。
- 非基于梯度的攻击。除了梯度信息之外,攻击还可能在没有任何梯度信息的情况下破坏模型。众所周知,除了梯度之外,许多基于 强化学习的攻击方法 可以攻击基于长期奖励的模型[33],[85],[108]。有些工作还用 生成模型 构建对抗样本[14]、[23]、[47]。上述方法都可以对没有梯度信息的模型进行攻击,且都是对实际模型进行攻击。
数据目标。与模型目标攻击不同,数据目标攻击不攻击特定模型。当攻击者只能访问数据,但没有足够的模型信息时,就会发生此类攻击。当数据成为目标时,通常有两种设置。
- 模型中毒。无监督特征分析方法仍然可以在不了解训练方法的情况下从数据中获取有用的信息。即使数据受到很小的干扰,也可能使一般的训练方法失效。此外,后门攻击
是另一个相关的热门话题,攻击者仅在数据集中注入对抗信号,但不会破坏常规样本上的模型性能[141]、[165]。 - 统计信息。除了使用数据来训练模型之外,在许多研究中,研究人员还使用图数据的统计结果或模拟结果[38]、[127]、[172]。在这种情况下,攻击者可以根据捕获图数据上有价值的统计信息来破坏模型。例如,通过基于结构信息和分析修改不同社区之间的一些边,可以使社区在这种攻击下计数不准确[127]。
攻击知识
攻击者会收到不同的信息来攻击系统。基于此,我们可以表征现有攻击的危险程度。
- 白盒攻击。在这种情况下,攻击者可以获得所有信息并利用它来攻击系统,例如预测结果、梯度信息等。如果攻击者不首先完全破坏系统,攻击可能无法成功。
- 灰盒攻击。攻击者获得有限的信息来攻击系统。与白盒攻击相比,它对系统的危险性更大,因为攻击者只需要部分信息。
- 黑盒攻击。在此设置下,攻击者只能对部分样本进行黑盒查询。因此,攻击者一般无法对训练好的模型进行投毒攻击。然而,如果黑盒攻击能够起作用,那么与其他两种攻击相比,它将是最危险的攻击,因为攻击者可以用最有限的认知来攻击模型。
攻击目标
通常,攻击者希望破坏整个系统的性能,但有时他们更愿意攻击系统中的几个重要目标实例。根据攻击的目标:
- 可用性攻击。可用性攻击的对抗目标是 降低系统的总体性能。例如,通过给出修改预算,我们希望系统的性能下降最多作为最优的攻击策略。
- 完整性攻击。完整性攻击的对抗目标是 降低目标实例的性能。例如,在推荐系统中,我们希望模型不能成功预测两个目标用户之间的隐藏关系。然而,系统的总体性能与原始系统相同或相似。
在定位攻击设置下,可用性攻击比完整性攻击更容易检测。因此,有意义的可用性攻击研究通常是在躲避攻击的背景下进行的。
攻击任务
对应于图数据上的各种任务,我们展示了如何攻击每个任务并通过修改统一的公式来解释总体思路。
- 节点相关任务。如前所述,大多数攻击论文关注节点级任务,包括节点分类[21]、[33]、[121]、[139]、[146]、[176]、[178]和节点嵌入[10] ,[158]。主要区别在于节点嵌入使用每个节点的低维表示来进行对抗性攻击。通过将式(2)的 c i {c^i} ci 设置为节点目标的表示。
- 链接相关任务。其他几个现有的作品研究节点嵌入[10]、[25]、[108]或拓扑相似性[128]、[172]并将它们用于链接预测。与节点分类相比,链路预测需要使用不同的输入数据,其中 c i {c^i} ci 代表链路目标,即一对节点的信息。
- 图相关任务。与节点分类相比,图分类需要图表示而不是节点表示[33],[113],[141],[165]。通过将式(2)的 c i {c^i} ci 设置为图目标的表示。
总结:图上的攻击
在本小节中,我们分析现有作品的贡献和局限性。然后我们讨论该领域潜在的研究机会。
- 贡献。首先,我们在表 3 中列出了所有已发表的论文及其特征,然后将它们分类为表 1 中选定的主要主题。然后,我们总结了现有对抗性攻击的独特贡献。需要指出的是,由于我们讨论的 34 篇论文中有 11 篇是预印本,所以我们特别在表 3 中列出了地点。我们还首先使用策略和方法来区分攻击方法。策略是指攻击的高层设计理念,而方法则代表攻击者扰乱图数据所采取的具体方法。
- 图神经网络。大多数对抗性攻击都与图神经网络有关。[33]使用强化学习方法来发现对抗性攻击,与其他作品相比,这是唯一支持黑盒攻击的方法。[176]利用传统机器学习和深度学习研究了对抗性图样本。同时,他们是第一个也是唯一一个讨论属性图对抗性攻击的小组。 [25]、[108]主要用深度图卷积嵌入模型来攻击链接预测任务。[10]通过近似谱和使用梯度信息来攻击多个模型。[121]通过优化方法对攻击节点进行分类,系统地讨论了图数据的对抗性攻击。之前的工作主要集中在边或节点修改,而[139]也修改了节点特征并提出了对图卷积神经网络(GCN)的混合攻击[69]。除了梯度检查之外,[41]、[146]还使用一阶梯度优化和低秩近似来攻击 GCN,这使得攻击更加有效。[21]通过设计新的损失和近似谱来攻击一般的学习方法。 [57]将图攻击知识用于恶意软件检测问题,这表明各种基于图的应用程序容易受到对抗性攻击。在没有梯度检查和优化设计的情况下,[109]使用强化学习来攻击GCN。然而,它包含一个明显的问题,即需要通过注入新节点来破坏图结构。[75]试图通过攻击图自动编码器模型来隐藏社区中的节点。这项工作没有使用梯度检查或其他优化方法,而是利用代理社区检测模型来实现攻击目标。最近的工作研究了 GNN 在后门攻击下的脆弱性 [141]、[165]。后门攻击修改训练数据中触发器的标签(例如具有典型模式的子图),其目的是使 GNN 对这些触发器进行错误分类,而不影响 GNN 在测试数据上的整体性能。
- 其他。尽管许多攻击工作都与 GNN 相关,但最近的许多论文开始关注对图数据的其他类型的对抗性攻击。[32]是最早对图数据进行攻击的工作之一,并且它也首次提出了无监督学习设置中的攻击方法。[127]首先通过基于启发式方法的边重写来攻击社区检测。[128]基于启发式方法的受攻击链接预测,该方法基于相似性度量。[172]使用贪婪方法来攻击基于局部和全局相似性度量的链接预测。除了传统的图应用之外,[158]首先攻击了知识图谱,破坏了基本的关系图预测模型。[22]基于遗传算法攻击社区检测。与以前的方法不同,它在攻击数据时选择使用重新布线而不是添加/删除边缘。[47]使用生成方法创建新的同构网络来攻击节点分类。除了之前的所有工作之外,[38]开始通过理论分析 来研究攻击,我们相信在这个领域将会看到更多的理论工作。它们可以帮助我们更好地理解图数据上的攻击。除了上述应用之外,推荐系统[44]、[95]、[160]、欺诈检测[17]、[39]、意见动态[31]、[48]和图分类[113]中的攻击图,[141]、[165]任务也引起了研究人员的关注。
- 局限。大多数当前工作的局限性总结如下。现有的大多数工作都没有对预算和距离的设置给出非常明确的策略,并在实际应用中给出合理的解释。与其他对抗性攻击不同,大多数图修改在现实生活中很难被人类注意到。为了解决这个问题,我们在第 5 节中对扰动和评估指标进行了更详细的讨论。同时,关于图不可感知的评估指标,大多数论文[10]、[25]、[33]都使用一种指标进行攻击,但这些对抗性样本可以通过其他现有的不可感知的评估指标来检测。在这项工作中,我们列出了 所有现有的评估指标,并建议未来的对抗性样本通过更多列出的评估指标变得难以察觉。另一个主要问题是由于问题表述不同。为此,我们对本次调查中讨论的所有现有作品给出了统一的问题表述。
- 最近的工作。对于最近提出的攻击方法,像以前的工作一样,添加边和修改节点特征等不可察觉的扰动也是主要方法。对于防御模型,一些研究人员[30]、[79]、[80]首先尝试提出新的邻域聚合模式,以保证对抗性攻击下的理论鲁棒性,而不是以前常用的对抗性训练技术。
- 未来发展方向。图数据的对抗性攻击是一个新的热门领域,潜在的研究机会总结如下:1)实践中,大多数图都与节点或边上的属性或更复杂的内容相关联。然而,很少有研究针对属性图(例如异构信息网络和网络图)精心设计对抗性攻击。2)一些先进的思想可以应用于 生成对抗样本,例如同态图。3)各种学习设置尚未得到充分研究,例如 图级攻击 和 节点级攻击的归纳学习。4)大多数现有攻击在其模型中没有考虑各种不可察觉性指标。在不同的任务中需要简洁而全面的不可感知性指标。一个好的、可解释的评估指标可以很容易地发现更多由当前方法创建的现有对抗样本。5)最后但并非最不重要的一点是,高质量对抗样本的距离或相似性度量在该领域尚未得到很好的研究。
图数据的对抗性防御
借助图数据,最近对对抗性攻击的深入研究也引发了对抗性防御的研究。在这里,我们调查了这一领域的现有工作,并将它们分为 对抗训练 和 攻击检测 两个流行的类别。在它们之后,我们使用附加的“其他方法”小节来总结不属于这两个通用类别的其余方法。
对抗性训练
虽然攻击者广泛使用对抗性攻击来执行有效的对抗性入侵,但防御者也可以使用同一把剑来提高其模型对抗对抗性攻击的鲁棒性[51]。在图设置中,我们通过稍微修改我们的对抗性攻击的统一表述来制定对抗性防御的目标,即等式:
min θ max G ^ c i ∈ Φ ( G i ) ∑ i L ( f θ ( c i , G ^ c i ) , y i ) \mathop {\min }\limits_\theta \mathop {\max }\limits_{{{\hat G}^{{c_i}}} \in \Phi ({G_i})} \sum\limits_i {L({f_\theta }({c_i},{{\hat G}^{{c_i}}}),{y_i})} θminG^ci∈Φ(Gi)maxi∑L(fθ(ci,G^ci),yi)
其中,符号的含义与第 3 节中定义的相同。这个想法是在训练期间交替优化两个竞争模块,其中攻击者试图通过在图上生成对抗性扰动 G ^ \hat G G^ 来最大化面向任务的损失,而防御者试图通过学习更鲁棒的图模型参数 θ \theta θ 来最小化相同的损失。通过这种方式,学习到的图模型有望抵御未来的对抗性攻击。
结构扰动。扰动图的最早也是最原始的方法是随机丢弃边[33]。这种廉价的对抗性扰动的联合训练被证明可以稍微提高标准 GNN 模型对图和节点分类任务的鲁棒性。更进一步,[146]提出了一种基于投影梯度下降的拓扑攻击生成方法来优化边扰动。拓扑攻击被证明可以提高对抗性训练的 GNN 模型针对不同的基于梯度的攻击和贪婪攻击的鲁棒性[125]、[146]、[172],而不会牺牲原始图上的节点分类准确性。同时,[34]提出通过最大化嵌入空间中随机噪声的影响以无监督的方式学习扰动,这提高了DeepWalk[96]在节点分类上的泛化性能。针对基于相似性的链接预测,[171] 形式化了贝叶斯 Stackelberg 游戏,以优化最鲁棒的链接,以保留对手删除剩余链接的情况。
属性扰动。除了链接之外,[36]、[45]、[105]还扰乱节点特征以启用虚拟对抗训练[91],从而增强原始节点和对抗节点之间的平滑性。特别是,[45] 设计了一个动态正则化器,迫使 GNN 模型学习以防止图上扰动的传播,而 [105] 在最敏感的方向上平滑 GCN 以提高泛化能力。[36]进一步批量进行虚拟对抗训练,以感知每个采样子集中节点之间的连接模式。[124] 利用对抗性对比学习 [15] 来解决 GNN 模型由于训练数据稀缺而面临对抗性攻击的漏洞,并应用条件 GAN 来利用图级辅助信息。[126]提出通过忽略离散性来直接扰动邻接矩阵和特征矩阵,而不是近似离散图空间,而[63]提出关注GNN模型的第一隐藏层来连续扰动邻接矩阵和特征矩阵。这些框架都被证明可以改进节点分类任务上的 GNN 模型。
面向攻击的扰动。基于现有的网络对抗攻击方法,如FGA [27]和Nettack [176],[26]设计了带有额外平滑防御策略的对抗训练流程。该流程被证明可以改进 GNN 模型,以应对节点分类和社区检测任务的不同对抗性攻击。[39]采用强化学习来训练针对论文中提出的混合攻击的鲁棒检测器。
攻击检测
另一种有效的防御方法是在 已知数据被污染的假设下检测并消除(或减少攻击的影响),而不是在训练期间产生对抗性攻击。由于图数据的复杂性,可以基于各种专业但直观的原则利用连接结构和辅助特征,从根本上区分干净数据和恶意数据,并抵御某些类型的攻击。
图预处理。[148]提出了基于图生成模型、链接预测和异常值检测的不同方法来检测潜在的恶意边。[59]提出基于随机抽取的节点子集计算的图感知标准来过滤掉被异常节点污染的节点集,而不是边;[163]提出基于对节点与其邻居的邻近分布之间的差异的实证分析来检测受拓扑扰动的节点(特别是 Nettack [176])。这些模型仅依赖网络拓扑进行攻击检测。在属性图上,根据观察到攻击者更喜欢添加边而不是删除边,并且边通常在不同的节点之间添加,[139]建议计算 Jaccard 相似度以删除可疑节点之间的可疑边。 [147]从中毒的训练数据中采样子图,然后采用异常值检测方法来检测和过滤对抗性边。所有这些模型都可以在训练 GNN 等普通图模型之前用于图预处理。
模型训练。有几项工作不是在训练前直接检测可疑节点或边,而是 设计了特定的注意机制来在训练期间动态发现和降低可疑数据的权重。[174]假设对抗性节点的预测不确定性较高,并根据基于高斯的 GCN 中的嵌入方差计算注意力权重。[115]建议基于 Nettack [176] 生成的真实有毒链接来训练攻击感知 GCN,并基于元学习转移为有毒链接分配小注意力权重的能力。
稳健性认证。与检测攻击相反,[11]、[179]设计了鲁棒性证书来衡量单个节点在对抗性扰动下的安全性。特别是,[11]考虑了结构扰动,而[179]考虑了属性扰动。与这些证书联合训练 GNN 模型可以为更多节点带来严格的安全保证。[62]从不同的角度推导了结构扰动下的群落检测方法的鲁棒性证明。[68]证明多项式谱图滤波器在结构扰动下是稳定的。
复杂图。除了传统的同质图之外,[97]研究了知识图链接预测模型对对抗性事实(链接)和事实识别的敏感性。[57]研究了异构图中中毒节点的检测,以增强Android恶意软件检测系统的鲁棒性。
其他方法
现在我们总结一下剩下的图对抗防御算法,这些算法既不是基于对抗训练,也不是针对攻击检测。根据它们对图数据和图模型的修改,我们进一步将它们分为三个子类别。
数据修改。我们提出了几种可用于修改图数据的攻击检测算法,即图预处理[59]、[148]、[163]。存在修改图数据而不直接检测攻击的方法。基于 Nettack [176] 仅影响图的高秩奇异分量的见解,[41] 提出通过在训练 GNN 模型之前计算图的低秩近似来减少攻击的影响。[47]提出了一种增强训练过程,通过生成更多结构噪声图来训练 GNN 模型以提高鲁棒性,并表明它对于节点的结构角色识别是有效的。[89] 分析了图的拓扑特征,并提出了两种训练数据选择技术,以提高对节点分类的有效对抗扰动的难度。这些方法都仅基于图拓扑,并且仅修改图数据而不是图模型。[156]利用变分图自动编码器从扰动图中重建图结构,其中重建的图可以减少对抗性扰动的影响。
模型修改。相反,存在仅修改图模型的方法,例如 模型结构重新设计 或 损失函数重新设计。最简单的方法是重新设计损失函数。从一些现有的工作来看,结果表明一些损失函数相对于对抗性示例表现出更好的性能。例如,[64]设计了一种基于图幂的替代算子,以取代 GNN 模型中的经典拉普拉斯算子,并提高了谱鲁棒性。他们证明了该算子与普通 GCN 的结合可以有效地进行节点分类和防御躲避攻击。[95]提出了一种分层 GCN 模型来聚合来自不同顺序的邻居,并在聚合过程中随机丢弃邻居消息。这种机制可以提高基于 GCN 的协同过滤模型的鲁棒性。 [161]介绍了邻居重要性估计和可以与 GNN 集成的分层图内存组件。这两个组件可以帮助提高 GNN 模型针对各种攻击的鲁棒性。
混合修改。更进一步,一些方法同时修改图数据和图模型。[60] 设计了一种边抖动方法,通过多个随机边翻转的图来恢复未扰动的节点邻域,并提出了一种自适应的GCN模型,该模型学习将多个图组合在一起。所提出的框架被证明可以提高 GCN 对节点分类(特别是蛋白质功能预测)的性能和鲁棒性。[88]提出了一种启发式方法,根据节点的度和连接模式迭代选择训练数据。进一步提出结合节点属性和结构特征,使用SVM代替任何GNN模型进行节点分类。在稀疏性、等级和特征平滑度等图属性的指导下,[67]提出了 Pro-GNN,它联合学习干净的图结构并一起训练鲁棒的 GNN 模型。
总结:图上的防御
从防御者的角度来看,可以在知道或不知道具体攻击的情况下设计防御方法。因此,当前的防御工作可以分为两类:1)与攻击无关的防御 旨在增强图模型针对任何可能的攻击而不是固定攻击的鲁棒性。2)针对攻击的防御 是根据特定攻击的特点而设计的。与面向攻击的攻击相比,攻击不可知的防御通常具有更广泛的攻击假设空间。最后,我们讨论该领域对抗性防御的一些未来机会。
与攻击无关的防御。正如我们在 4.1 节中总结的那样,对抗性训练是攻击不可知防御方法的典型实例[33]、[36]、[45]、[105]、[146]。它通常会在图结构或模型上生成简单的扰动来训练防御模型。在测试阶段,以这种方式训练的一些模型可以对这些扰动表现出良好的鲁棒性。以这种方式训练的一些方法[146]甚至可以针对其他特定攻击(例如[178]中提出的Meta-self)获得良好的防御性能。请注意,防御方法是在不了解其他新攻击的情况下设计和训练的。
除了对抗性训练之外,其他工作还通过对攻击策略和结果的启发式假设来保护图模型。[115]假设有未污染的图来帮助检测攻击。[57]、[61]、[64]、[174]提出了新的 GNN 架构来增强其鲁棒性。 [88]、[89]直接策划最佳训练集以减轻训练模型的脆弱性。
针对攻击的防御。面向攻击的防御是根据特定攻击的策略和方法而设计的。即,防御者充分了解攻击方法,防御方法可以检测到相应的攻击或遏制其性能。目前的防御工作中,[41]首先论证了Nettack的弱点[176],并利用SVD来防御Nettack。 [63]分析了Nettack[176]和RLS2V[33]的策略和方法,并提出了一种对抗性训练方法。[139]检查了两种基于梯度的攻击(即FGSM [51]和JSMA [94]),并在模型训练期间应用边丢弃技术来减轻此类攻击的影响。与攻击无关的防御类似,一些面向攻击的方法表现出良好的可生成性,这意味着它可以防御其他未知的攻击。例如,[139]中提出的防御方法也可以防御Nettack。结合表4中的"Corresp. Attack"列,我们可以看到 Nettack和RL-S2V已成为防御设计和评估的基准攻击方法。一些工作采用极小极大博弈[48]或优化[11]、[62]、[179]的框架来证明图模型在给定攻击和防御下的鲁棒性界限。这类防御工作是面向攻击的,因为它们承担了特定的攻击。
最近的工作。除了节点分类和链接预测等常见任务之外,还提出了针对图对齐任务(例如图匹配)的攻击[167]和防御[100]、[169]、[173]。
局限性和未来方向。我们一直关注现有不同作品对图对抗防御的贡献。现在我们总结了在这方面研究中观察到的一些常见局限性,并暗示了未来的方向:1)大多数防御模型专注于节点级任务,尤其是节点分类,而更多地关注链接和图级任务(例如链接预测和图分类)可能会很有趣。在基于图的搜索、推荐、广告等更现实的任务中也有很大的潜力。2)虽然现在的网络数据往往与复杂的内容(例如时间戳、图像、文本)相关联,但 现有的防御模型几乎没有考虑动态或其他内容丰富的复杂网络系统 设置下的攻击和防御的效果。3)大多数防御模型尤其与 GNN 或 GCN 相关,但还有许多其他图模型和分析方法,可能使用更广泛但研究较少(例如,基于随机游走的模型、随机块模型和许多计算图属性) 。他们如何敏感并容易受到图对抗性攻击? GNN 模型的改进能否转移并推广到这些传统方法和措施? 4)大多数现有工作没有研究防御模型的效率和可扩展性。众所周知,现实世界的网络可能是巨大的并且经常频繁地演化,因此如何有效地学习模型并适应变化对于防御者来说非常重要。5)虽然节点分类和链路预测等下游任务有标准的评估协议和优化目标,但防御方法是针对准确性、鲁棒性、泛化性等异构目标进行优化的,并且它们倾向于定义自己的实验设置和指标,提出公平和全面的评估具有挑战性。
指标
在本节中,我们总结了评估 图数据攻击 和 防御性能 的指标。我们首先简要介绍一般评估指标以及它们在对抗性能评估中的具体用法的一些说明。然后我们详细介绍了针对攻击和防御设计的特定评估指标。
一般指标
基于准确性的指标
根据表3和表4,许多现有的工作解决节点分类问题,这通常是二元或多类分类问题。现有的工作都使用基于准确度的指标,如 准确度、召回率、精确度和 F1 分数,从不同角度反映分类准确度。读者可以参考[131]来获取这些指标的详细解释。请注意,[32]、[121] 使用的假阴性率 (FNR) 和假阳性率 (FPR) 是从混淆矩阵导出的两个指标。FNR是所有实际正例中假负例的百分比,描述了分类器漏掉正例的比例。同样,FPR反映了分类器错误分类的负实例的比例。调整兰德指数(ARI)[136]是一种基于准确性的度量,不依赖标签信息。[23]使用它来测量图中两个簇之间的相似性。
除了上述指标之外,ROC曲线下面积(AUC)[137]和 平均精度(AP)[130]也被广泛使用,例如[59]、[108]、[128]、[148] ],[174]。AUC 对正实例的概率排名敏感,根据分类器的预测概率,当正实例排名高于负实例时,AUC 较大。AP 是平衡精度和召回率的指标,当召回率阈值从 0 增加到 1 时,精度越高,AP 越高。这两个指标可以更好地将分类性能反映为单个分数,因为它们提供了对所有实例的预测概率的全面评估。
基于排名的指标
平均倒数排名(MRR)[132]和 Hits@K 是[97]、[158]用来评估知识图上链接预测性能的两个排名指标。给定针对一个查询检索到的项目列表,并按其概率排名,查询响应的倒数排名是第一个正确项目的排名的倒数:第一名为 1,第二名为 1⁄2,第三名为 1⁄3,以此类推。Hits@K 是排名列表中前 K 项中正确答案的数量。它也可以用来评估推荐系统的性能[44]。nDCG@K [135]是评估推荐模型鲁棒性的另一个指标[95]。
基于图的指标
基于图的度量指示图的特定属性。归一化互信息(NMI)[134]和 模块化 [133]是[22]、[23]、[150]用来评估图上社区检测(即聚类)性能的两个指标。NMI源于信息论,衡量两个变量之间的相互依赖关系。在社区检测场景中,NMI 用于衡量两个社区之间的共享信息量(即相似度)。模块化旨在衡量将图划分为簇的强度。具有高模块化度的图在簇内的节点之间具有密集的连接,但在不同簇内的节点之间具有稀疏的连接。
[109]采用一些图属性统计数据作为度量来评估攻击者改变图的程度(即攻击的不可察觉性)。这些指标包括基尼系数、特征路径长度、分布熵、幂律指数和三角形计数。有关这些指标的更多详细信息,请参阅[12]。更多的图形统计指标包括[127]使用的度排名、紧密度排名、介数排名以及[149]使用的聚类系数、最短路径长度、对角距离。
对抗指标
除了上述通用指标之外,现有工作还提出或使用了许多衡量图数据攻击和防御性能的指标。我们首先介绍广泛使用的指标的详细公式和描述,然后简要总结特定论文使用的一些独特指标。每个指标名称后面的参考文献是指第一篇提出或使用该指标的论文,括号内的参考文献是指使用该指标的其他攻击和防御论文。
通用指标
攻击成功率 (ASR) [32] ( [14], [24], [25], [27], [28], [63], [85], [112], [125], [141], [155],[165])。 ASR 是衡量攻击方法性能的最常用指标:
A S R = # S u c c e s s f u l _ a t t a c k s # A l l _ a t t a c k s ASR = \frac{{\# Successful\_attacks}}{{\# All\_attacks}} ASR=#All_attacks#Successful_attacks
分类边际(CM) [176]([88],[124],[139],[163],[177])。 CM衡量了完整性攻击的性能:
C M ( t ) = p t , c t − max c ≠ c t p t , c t CM(t) = {p_{t,{c_t}}} - \mathop {\max }\limits_{c \ne {c_t}} {p_{t,{c_t}}} CM(t)=pt,ct−c=ctmaxpt,ct
其中, t t t 是目标实例, c t {c_t} ct 是 t t t 的真实类别, p t , c {p_{t,c}} pt,c 是 t t t 为 c c c 的概率。上式计算真实类别概率与其他类别概率之间的最大差异。换句话说,它显示了攻击翻转目标实例的预测类别的程度。[88] 提出了 CM 的另一版本:
C M ( t ) = log p t , c t max c ≠ c t p t , c CM(t) = \log \frac{{{p_{t,{c_t}}}}}{{{{\max }_{c \ne {c_t}}}{p_{t,c}}}} CM(t)=logmaxc=ctpt,cpt,ct
当实例分类正确时,CM将为正;否则将为负值。
正确/错误分类率 [10]([41]、[113]、[126]、[146]、[178])。这两个指标根据所有实例的分类结果来评估攻击/防御性能。
M C R = # M i s c l a s s i f i e d _ i n s tan c e s # A l l _ i n s tan c e s MCR = \frac{{\# Misclassified\_ins\tan ces}}{{\# All\_ins\tan ces}} MCR=#All_instances#Misclassified_instances
C C R = 1 − M C R CCR = 1 - MCR CCR=1−MCR
攻击预算 [88]([38],[89])。攻击者预算是衡量攻击者实现其目标所需的最小扰动的通用指标。值越小,攻击性能越好,防御性能越差。[38]将移除的边数作为攻击者预算。[88]、[89]以采用最小数量的扰动让攻击者成功地导致目标被错误分类为预算。
平均修改链接 (AML) [27]([25]、[27]、[28]、[155])。AML 是上面介绍的攻击预算的变体。它描述了攻击者为实现攻击目标所需的修改链接的平均数量:
A M L = # M o d i f i e d _ l i n k s # A l l _ a t t a c k s AML = \frac{{\# Modified\_links}}{{\# All\_attacks}} AML=#All_attacks#Modified_links
隐蔽措施 [127]([75]、[128]、[149])。隐藏措施用于评估图中隐藏节点或社区的性能[75]、[127]、[128]。从另一个角度来看,攻击引入的结构变化也可以用来量化攻击的隐蔽性[149]。
相似度得分 [108]([172])。相似度分数是衡量给定 实例对 相似度的通用指标。它可以用作完整性攻击的目标,攻击者的目标是增加或减少目标实例对的相似度分数。对于图中的节点实例,其局部结构和节点嵌入都可以用于计算相似度得分。
具体指标
平均最坏情况边际(AWM)[11]。最坏情况边际是上述定义的分类边际的最小值。AWM 意味着该值是在每个数据批次的最坏情况边际上取平均得到的。
鲁棒性优点(RM)[64]。RM 是指提出的防御方法的攻击后准确率与原始 GCN 模型的攻击后准确率之间的差异。数值越大表示防御性能越好。
攻击恶化(AD)[64]。 AD 是攻击后准确率下降量与无攻击时准确率的比率。
平均防御率(ADR)[26]。 ADR 是根据上面定义的 ASR 评估防御性能的指标。它比较应用或不应用防御方法的攻击后的 ASR。
平均置信度差异(ACD)[26]。ACD 是一种评估防御性能的度量,基于一组节点在攻击之前和之后的分类边际的平均差异。这样的节点集合包括攻击之前被正确分类的节点。
破坏防止比率(DPR)[171]。破坏防止度量了防御措施可以预防的损害量。设 L 0 L0 L0 为在没有攻击时防守者的累积损失。设 L A LA LA 为在某种攻击 A A A 下防守者在不能进行可靠查询时的损失。 L D LD LD 表示防御者按照一定的防御策略 D D D 进行可靠查询时的损失。DPR可以定义如下:
D P R A D = L A − L D L A − L 0 DPR_A^D = \frac{{LA - LD}}{{LA - L0}} DPRAD=LA−L0LA−LD
认证准确性 [62]。这是提出用于评估社区检测模型对抗对抗攻击的认证方法的。认证准确性 C K ( l ) CK(l) CK(l) 是指在图中添加或删除最多 l l l 条边时,所提出的方法可以明确 检测到的受害节点集合的比例,这些节点在同一个社区中。
实际效果 [39]。由于攻击者可能会瞄准攻击的实际效果,例如增加物品收入或声誉,因此[39]提出了一种基于收入的指标,从实际角度衡量攻击和防御的性能。
数据集和应用
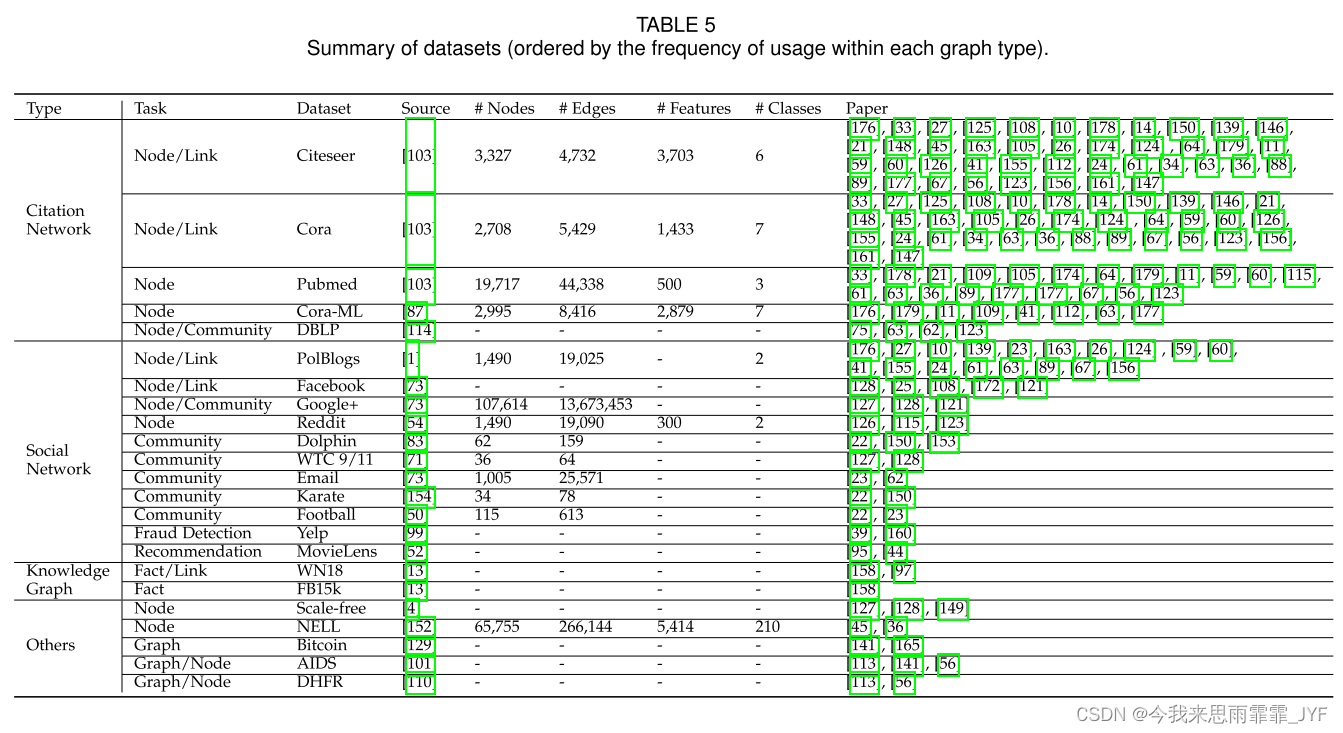
表 5 总结了图数据对抗性攻击和防御工作中使用的一些常见数据集。前四个引文图在之前的工作中被广泛用作节点分类基准[69]、[117]、[118]、[138]。 [108]还研究了 Cora 和 Citeseer 上的对抗性链接预测问题。DBLP 包括具有更多元数据信息的多个引文数据集。因此它可以用来研究社区发现任务[62]。在社交网络数据集中,PolBlogs 是另一个特别在对抗性设置中使用的数据集,其中博客是节点,它们的交叉引用是边。与引文数据集相比,Reddit 和 Facebook 是两个更大的图数据集。由于不同论文使用了多个版本的 Facebook 数据集,因此我们省略了其统计数据。WTC 9/11、Email、Dolphin、Karate 和 Football 是社区检测的五个基准数据集。最近的一些工作还基于 Yelp 和 MovieLens 数据研究了推荐系统 [44]、[95] 和评论系统 [39]、[160] 的攻击和防御。[97]、[158]使用两个知识图基准 WN18 和 FB15k 研究了知识图的对抗性攻击和防御。无标度网络是图生成模型合成的典型图类型。有些作品还采用其他图生成模型(如 Erd˝os-Rényi 模型)来生成图以方便他们的实验 [17]、[31]、[68]、[127]、[128]、[165]、[172]。除了节点级任务之外,包含多个图的比特币、艾滋病和 DHFR 数据集也被用来研究图分类模型的鲁棒性[56]、[113]、[141]、[165]。其中,Bitcoin 是比特币交易数据集,AIDS 包含生物图来表示不同生物化合物的抗病毒特性,DHFR 包含图来表示化学键类型。
未来发展方向。除了表5中列出的数据集之外,值得注意的是其他一些不太受关注但可以在未来研究中研究的数据集。据我们所知,[57]是第一篇也是唯一一篇研究 异构信息网络(HIN)脆弱性 的论文,异构信息网络是一种具有异构节点和边类型的图模型[104]。尽管 HIN 已应用于许多安全应用程序,例如恶意用户检测 [162]、垃圾邮件检测 [74] 和金融欺诈检测 [58],但其针对对抗性攻击的鲁棒性在很大程度上仍未得到探索。最近的一项研究[48]首先给出了对具有谱形式的图上的意见传播的对抗性攻击的表述,可用于研究社交网络的意见动态。 [97]、[158]是研究知识图(KG)模型的对抗性攻击和防御的前两篇作品。随着近年来 KG 研究的兴起,其安全问题也需要引起关注。动态图模型的安全性 [28]也是另一个研究途径。
除了上述工作和数据集之外,关于许多其他图类型及其相关应用的安全问题的讨论很少。仅举几例,生物图、因果图和二分图 引起了广泛的研究关注,但很少有工作研究这些图的潜在攻击及其对策。从应用的角度来看,随着 GNN 已成功应用于推荐系统、计算机视觉和自然语言处理[140],这些 特定应用下对图数据的对抗性攻击和防御 是另一个有前景且具有实际影响的研究方向。
结论
在这项工作中,我们涵盖了当今我们所知的关于图数据的对抗性攻击和防御的最多发布的论文。我们首先给出图数据对抗性学习的统一问题表述,并给出定义和分类法以对多个级别的文献进行分类。接下来,我们总结了大多数现有的不可察觉扰动评估指标、数据集,并讨论了有关不可察觉指标的几个原则。然后,我们分析现有作品的贡献和局限性。最后,我们概述了这项工作可能带来的有前景的未来研究方向和机会。






)




 xTS介绍)







