或许在生活中，经常会碰到针对某一个问题，在众多的限制条件下，如何去寻找一个最优解？可能大家想到了很多诸如“线性规划”，“动态规划”这些经典策略，当然有的问题我们可以用贪心来寻求整体最优解，在图论中一个典型的贪心法求最优解的例子就莫过于“最短路径”的问题。

一、概序

从下图中我要寻找 V0 到 V3 的最短路径，你会发现通往他们的两点路径有很多：V0->V4->V3，V0->V1->V3，当然你会认为前者是你要找的最短路径，那如果说图的顶点非常多，你还会这么轻易的找到吗？下面我们就要将刚才我们那点贪心的思维系统的整理下。

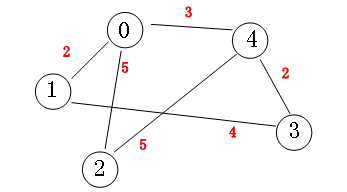
二、构建

如果大家已经了解 Prim 算法，那么 Dijkstra 算法只是在它的上面延伸了下，其实也是很简单的。

2.1、边节点

这里有点不一样的地方就是我在边上面定义一个 vertexs 来记录贪心搜索到某一个节点时曾经走过的节点，比如从 V0 贪心搜索到 V3 时，我们 V3 的 vertexs 可能存放着 V0,V4,V3 这些曾今走过的节点，或许最后这三个节点就是我们要寻找的最短路径。

 #region 边的信息/// <summary>/// 边的信息/// </summary>public class Edge{//开始边public int startEdge;//结束边public int endEdge;//权重public int weight;//是否使用public bool isUse;//累计顶点public HashSet<int> vertexs = new HashSet<int>();}#endregion

2.2、Dijkstra 算法

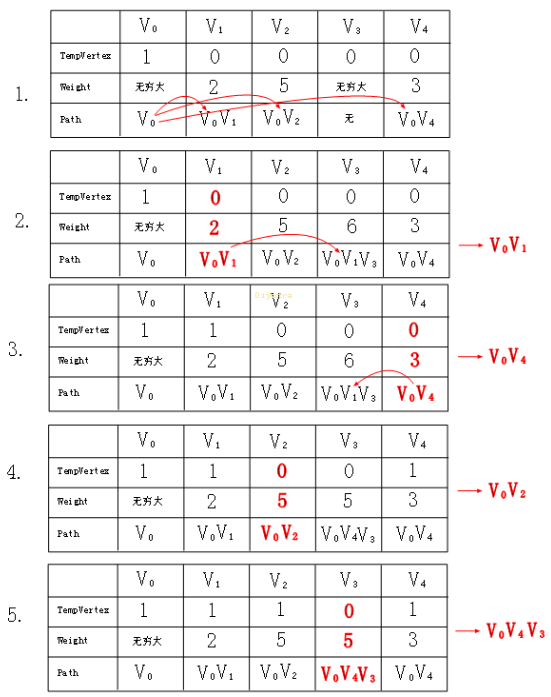
首先我们分析下 Dijkstra 算法的步骤：
有集合 M={V0,V1,V2,V3,V4}这样 5 个元素，我们用 TempVertex 表示该顶点是否使用。
Weight 表示该 Path 的权重(默认都为 MaxValue)。
Path 表示该顶点的总权重。
①. 从集合 M 中挑选顶点 V0 为起始点。给 V0 的所有邻接点赋值，要赋值的前提是要赋值的 weight 要小于原始的 weight，并且排除已经访问过的顶点，然后挑选当前最小的 weight 作为下一次贪心搜索的起点，就这样 V0V1 为挑选为最短路径，如图 2。
②. 我们继续从 V1 这个顶点开始给邻接点以同样的方式赋值，最后我们发现 V0V4 为最短路径。也就是图 3。
……
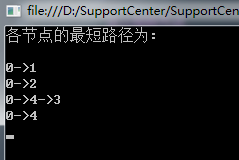
③. 最后所有顶点的最短路径就这样求出来了 。

 #region Dijkstra算法/// <summary>/// Dijkstra算法/// </summary>public Dictionary<int, Edge> Dijkstra(){//收集顶点的相邻边Dictionary<int, Edge> dic_edges = new Dictionary<int, Edge>();//weight=MaxValue:标识没有边for (int i = 0; i < graph.vertexsNum; i++){//起始边var startEdge = i;dic_edges.Add(startEdge, new Edge() { weight = int.MaxValue });}//取第一个顶点var start = 0;for (int i = 0; i < graph.vertexsNum; i++){//标记该顶点已经使用过dic_edges[start].isUse = true;for (int j = 1; j < graph.vertexsNum; j++){var end = j;//取到相邻边的权重var weight = graph.edges[start, end];//赋较小的权重if (weight < dic_edges[end].weight){//与上一个顶点的权值累加var totalweight = dic_edges[start].weight == int.MaxValue ? weight : dic_edges[start].weight + weight;if (totalweight < dic_edges[end].weight){//将该顶点的相邻边加入到集合中dic_edges[end] = new Edge(){startEdge = start,endEdge = end,weight = totalweight};//将上一个边的节点的vertex累加dic_edges[end].vertexs = new HashSet<int>(dic_edges[start].vertexs);dic_edges[end].vertexs.Add(start);dic_edges[end].vertexs.Add(end);}}}var min = int.MaxValue;//下一个进行比较的顶点int minkey = 0;//取start邻接边中的最小值foreach (var key in dic_edges.Keys){//取当前 最小的 key(使用过的除外)if (min > dic_edges[key].weight && !dic_edges[key].isUse){min = dic_edges[key].weight;minkey = key;}}//从邻接边的顶点再开始找start = minkey;}return dic_edges;}#endregion