进行科学计算时,最重要的一个问题是对联立线性方程组求解。在矩阵表示法中,常见问题采用以下形式:给定两个矩阵 A 和 b,是否存在一个唯一矩阵 x 使 Ax = b 或 xA = b?
考虑一维示例具有指导意义。例如,方程
7x = 21
是否具有唯一解?
答案当然是肯定的。方程有唯一解 x = 3。通过除法很容易求得该解:
x = 21/7 = 3。
该解通常不是通过计算 7 的倒数求得的,即先计算 7 –1 = 0.142857...,然后将 7 –1 乘以 21。这将需要更多的工作,而且如果 7 –1 以有限位数表示时,准确性会较低。类似注意事项也适用于多个未知数的线性方程组;MATLAB 在解此类方程时不会计算矩阵的逆。
尽管这不是标准的数学表示法,但 MATLAB 使用标量示例中常见的除法术语来描述常规联立方程组的解。斜杠 / 和反斜杠 \ 这两个除号分别对应 MATLAB 函数 mrdivide 和 mldivide。两种运算符分别用于未知矩阵出现在系数矩阵左侧或右侧的情况:
x = b/A
表示使用 mrdivide 获得的矩阵方程 xA = b 的解。
x = A\b
表示使用 mldivide 获得的矩阵方程 Ax = b 的解。
考虑将方程 Ax = b 或 xA = b 的两端“除以”A。系数矩阵 A 始终位于“分母”中。
x = A\b 的维度兼容性条件要求两个矩阵 A 和 b 的行数相同。这样,解 x 的列数便与 b 的列数相同,并且其行维度等于 A 的列维度。对于 x = b/A ,行和列的角色将会互换。
实际上,Ax=b 形式的线性方程组比 xA=b 形式的线性方程组更常见。因此,反斜杠的使用频率要远高于斜杠的使用频率。本节其余部分将重点介绍反斜杠运算符;斜杠运算符的对应属性可以从以下恒等式推知:
(b/A)' = (A'\b').
系数矩阵 A 不需要是方阵。如果 A 的大小为 m×n,则有三种情况:
m = n
方阵方程组。求精确解。
m > n
超定方程组,即方程个数多于未知数个数。求最小二乘解。
m < n
欠定方程组,即方程个数少于未知数个数。使用最多 m 个非零分量求基本解。
1mldivide 算法
mldivide 运算符使用不同的求解器来处理不同类型的系数矩阵。通过检查系数矩阵自动诊断各种情况。
线性方程组 Ax = b 的通解描述了所有可能的解。可以通过以下方法求通解:
1求对应的齐次方程组 Ax = 0 的解。使用 null 命令通过键入 null(A) 来执行此操作。这会将解空间的基向量恢复为 Ax = 0。任何解都是基向量的线性组合。
2求非齐次方程组 Ax = b 的特定解。然后,可将 Ax = b 的任何解写成第 2 步中的 Ax = b 的特定解加上第 1 步中的基向量的线性组合之和。本节其余部分将介绍如何使用 MATLAB 求 Ax = b 的特定解,如第 2 步中所述。
2方阵方程组
最常见的情况涉及到一个方阵系数矩阵 A 和一个右侧单列向量 b 。
2.1非奇异系数矩阵
如果矩阵 A 是非奇异矩阵,则解 x = A\b 的大小与 b 的大小相同。例如:
A = pascal(3);
u = [3; 1; 4];
x = A\u x =
10
-12
5
可以确认 A*x 恰好等于 u。如果 A 和 b 为方阵并且大小相同,则 x= A\b 也具有相同大小:
b = magic(3);
X = A\b X =
19 -3 -1
-17 4 13
6 0 -6
可以确认 A*x 恰好等于 b。以上两个示例具有确切的整数解。这是因为系数矩阵选为 pascal(3) ,这是满秩矩阵(非奇异的)。
2.2奇异系数矩阵
如果方阵 A 不包含线性无关的列,则该矩阵为奇异矩阵。如果 A 为奇异矩阵,则 Ax = b 的解将不存在或不唯一。如果 A 接近奇异或检测到完全奇异性,则反斜杠运算符 A\b 会发出警告。如果 A 为奇异矩阵并且 Ax = b 具有解,可以通过键入以下内容求不是唯一的特定解
P = pinv(A)*b pinv(A) 是 A 的伪逆。如果 Ax = b 没有精确解,则 pinv(A) 将返回最小二乘解。例如:
A = [ 1 3 7 ; -1 4 4 ; 1 10 18 ] 为奇异矩阵,可以通过键入以下内容进行验证:
rank(A) ans =
2
由于 A 不是满秩,它有一些等于零的奇异值。对于 b =[5;2;12] ,方程 Ax = b 具有精确解:
pinv(A)*b ans =
0.3850
-0.1103
0.7066
通过键入以下内容验证 pinv(A)*b 是否为精确解
A*pinv(A)*b ans =
5.0000
2.0000
12.0000
但是,如果 b = [3;6;0] ,则 Ax = b 没有精确解。在这种情况下, pinv(A)*b 会返回最小二
乘解。键入
A*pinv(A)*b ans =
-1.0000
4.0000
2.0000
则不会返回原始向量 b。通过得到增广矩阵 [A b] 的简化行阶梯形式,可以确定 Ax = b 是否具有精确解。为此,对于此示例请输入
rref([A b]) ans =
1.0000 0 2.2857 0
0 1.0000 1.5714 0
0 0 0 1.0000
由于最下面一行全部为零(最后一项除外),因此该方程无解。在这种情况下,pinv(A) 会返回最小二乘解。
3超定方程组
此示例说明在对试验数据的各种曲线拟合中通常会如何遇到超定方程组。在多个不同的时间值 t 对数量 y 进行测量以生成以下观测值。可以使用以下语句输入数据并在表中查看该数据。
t = [0 .3 .8 1.1 1.6 2.3]';
y = [.82 .72 .63 .60 .55 .50]';
B = table(t,y) B=6×2 table
t y
___ ____
0 0.82
0.3 0.72
0.8 0.63
1.1 0.6
1.6 0.55
2.3 0.5
尝试使用指数衰减函数对数据进行建模
上一方程表明,向量 y 应由两个其他向量的线性组合来逼近。一个是元素全部为 1 的常向量,另一个是带有分量 exp(-t) 的向量。未知系数 c 1 和 c 2 可以通过执行最小二乘拟合来计算,这样会最大限度地减小数据与模型偏差的平方和。在两个未知系数的情况下有六个方程,用 6×2 矩阵表示。
E = [ones(size(t)) exp(-t)] E = 6×2
1.0000 1.0000
1.0000 0.7408
1.0000 0.4493
1.0000 0.3329
1.0000 0.2019
1.0000 0.1003
使用反斜杠运算符获取最小二乘解。
c = E\y c = 2×1
0.4760
0.3413
也就是说,对数据的最小二乘拟合为
以下语句按固定间隔的 t 增量为模型求值,然后与原始数据一同绘制结果:
T = (0:0.1:2.5)';
Y = [ones(size(T)) exp(-T)]*c;
plot(T,Y,'-',t,y,'o')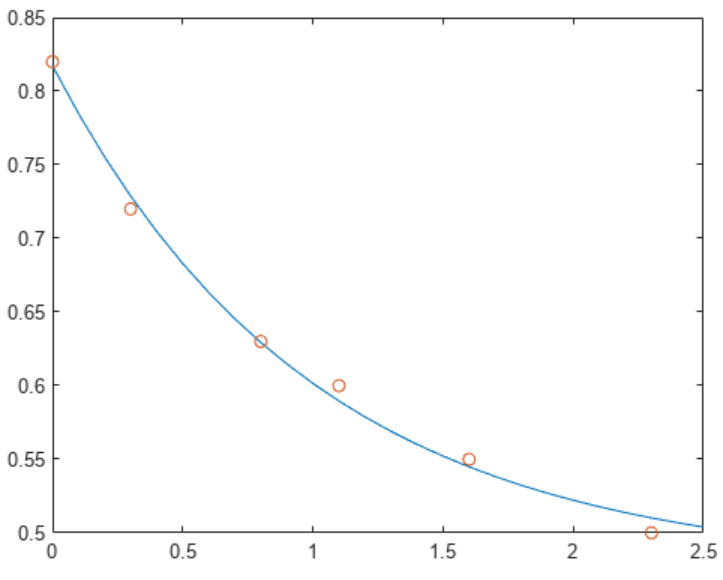
E*c 与 y 不完全相等,但差值可能远小于原始数据中的测量误差。如果矩形矩阵 A 没有线性无关的列,则该矩阵秩亏。如果 A 秩亏,则 AX = B 的最小二乘解不唯一。如果A 秩亏,则 A\B 会发出警告,并生成一个最小二乘解。您可以使用 lsqminnorm 求在所有解中具有最小范数的解 X 。
4欠定方程组
本例演示了欠定方程组的解不唯一的情况。欠定线性方程组包含的未知数比方程多。MATLAB 矩阵左除运算求基本最小二乘解,对于 m × n 系数矩阵,它最多有 m 个非零分量。
以下是一个简单的随机示例:
R = [6 8 7 3; 3 5 4 1]
rng(0);
b = randi(8,2,1) R =
6 8 7 3
3 5 4 1
b =
7
8
线性方程组 Rp = b 有两个方程,四个未知数。由于系数矩阵包含较小的整数,因此适合使用 format 命令以有理格式显示解。通过以下命令可获取特定解
format rat
p = R\b p =
0
17/7
0
-29/7
其中一个非零分量为 p(2) ,因为 R(:,2) 是具有最大范数的 R 的列。另一个非零分量为 p(4) ,因为 R(:,4) 在消除 R(:,2) 后起控制作用。欠定方程组的完全通解可以通过 p 加上任意零空间向量线性组合来表示,可以使用 null 函数(使用请求有理基的选项)计算该空间向量。
Z = null(R,'r') Z =
-1/2 -7/6
-1/2 1/2
1 0
0 1
可以确认 R*Z 为零,并且残差 R*x - b 远远小于任一向量 x(其中x = p + Z*q) 由于 Z 的列是零空间向量,因此 Z*q 是以下向量的线性组合:

为了说明这一点,选择任意 q 并构造 x,计算残差的范数。
q = [-2; 1];
x = p + Z*q;
format short
norm(R*x - b) ans =
2.6645e-15
如果有无限多个解,则最小范数解具有特别意义。您可以使用 lsqminnorm 计算最小范数最小二乘解。该解具有 norm(p) 的最小可能值。
p = lsqminnorm(R,b) p =
-207/137
365/137
79/137
-424/137
5多右端线性方程组的求解
某些问题涉及求解具有相同系数矩阵 A 但具有不同右端 b 的线性方程组。如果可以同时使用不同的 b 值,则可以将 b 构造为多列矩阵,并使用单个反斜杠命令求解所有方程组: X = A\[b1 b2 b3 …]。但是,有时不同的 b 值并非全部同时可用,也就是说,您需要连续求解若干方程组。如果使用斜杠 (/) 或反斜杠 (\) 求解其中一个方程组,则该运算符会对系数矩阵 A 进行分解,并使用此矩阵分解来求解。然而,随后每次使用不同的 b 求解类似方程组时,运算符都会对 A 进行同样的分解,而这是一次冗余计算。此问题的求解是预先计算 A 的分解,然后重新使用因子对 b 的不同值求解。但是,实际上,以这种方式预先计算分解可能很困难,因为需要知道要计算的分解(LU、LDL、Cholesky 等)以及如何乘以因子才能对问题求解。例如,使用 LU 分解,您需要求解两个线性方程组才能求解原始方程组 Ax = b:
[L,U] = lu(A);
x = U \ (L \ b); 对于具有若干连续右端的线性方程组,建议使用 decomposition 对象求解。借助这些对象,您可利用预先计算矩阵分解带来的性能优势,而不必了解如何使用矩阵因子。您可以将先前的 LU 分解替换为:
dA = decomposition(A,'lu');
x = dA\b; 如果您不确定要使用哪种分解,decomposition(A) 会根据 A 的属性选择正确的类型,类似于反斜杠的功能。
以下简单测试验证了此方法可能带来的性能优势。该测试分别使用反斜杠 (\) 和 decomposition 对同一稀疏线性方程组求解 100 次。
n = 1e3;
A = sprand(n,n,0.2) + speye(n);
b = ones(n,1);
% Backslash solution
tic
for k = 1:100
x = A\b;
end
toc Elapsed time is 9.006156 seconds.
% decomposition solution
tic
dA = decomposition(A);
for k = 1:100
x = dA\b;
end
toc Elapsed time is 0.374347 seconds.
对于这个问题,decomposition 求解比单独使用反斜杠要快得多,而语法仍然很简单。
6迭代法
如果系数矩阵 A 很大并且是稀疏矩阵,分解方法一般情况下将不会有效。迭代方法可生成一系列近似解。MATLAB 提供了多个迭代方法来处理大型的稀疏输入矩阵。
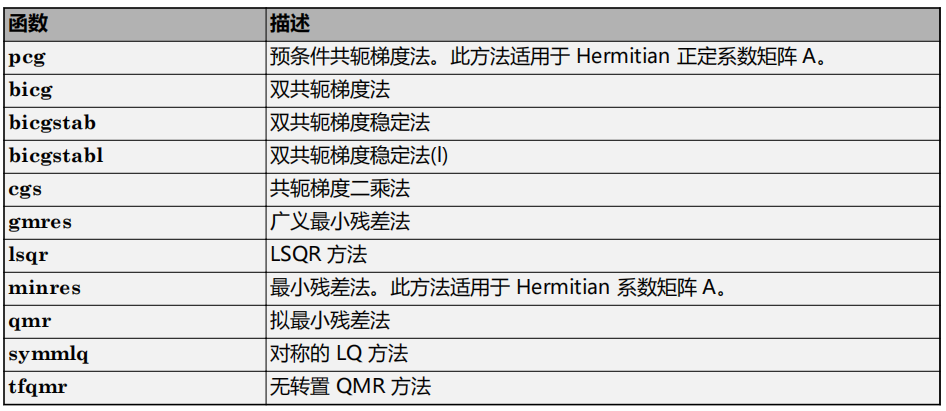
7多线程计算
对于许多线性代数函数和按元素的数值函数,MATLAB 软件支持多线程计算。这些函数将自动在多个线程上执行。要使函数或表达式在多个 CPU 上更快地执行,必须满足许多条件:
1 函数执行的运算可轻松划分为并发执行的多个部分。这些部分必须能够在进程之间几乎不通信的情况下执行。它们应需要很少的序列运算。
2数据大小足以使并发执行的任何优势在重要性方面超过对数据分区和管理各个执行线程所需的时间。例如,仅当数组包含数千个或以上的元素时,大多数函数才会加速。
3运算未与内存绑定;处理时间不受内存访问时间控制。一般而言,复杂函数比简单函数速度更快。如果启用多线程, inv 、 lscov 、 linsolve 和 mldivide 将会对大型双精度数组(约 10,000 个元素或更多)大幅增加速度。










)

)


)
)


