图像放大的三种插值算法
获取源工程可访问gitee可在此工程的基础上进行学习。
该工程的其他文章:
01- 一元熵值、二维熵值
02- 图像平移变换,图像缩放、图像裁剪、图像对角线镜像以及图像的旋转
03-邻域平均平滑算法、中值滤波算法、K近邻均值滤波器
04-分段线性变换,直方图均衡化、锐化处理
05-基于拉普拉斯算子、Canny的边缘检测功能、实现Otsu分割方法
文章目录
- 图像放大的三种插值算法
- 实验内容
- 一、 插值算法的原理
- 1. 最近邻插值
- 2. 双线性插值
- 3. 立方卷积插值
- 二、 实验代码与现象图
- 1. 最近邻插值
- 2. 双线性插值
- 3.立方卷积插值
实验内容
B–(3)研究放大图像时使用的插值算法,使用VC++实现常见的三种图像插值算法:最近邻插值,双线性插值,立方卷积插值。通过实验验证其效果。
一、 插值算法的原理
1. 最近邻插值
最近邻插值是一种简单的插值方法,它选择离目标位置最近的已知像素值。对于二维图像上的插值,最近邻插值的公式为:
I new ( x , y ) = I old ( round ( x ) , round ( y ) ) I_{\text{new}}(x, y) = I_{\text{old}}\left(\text{round}(x), \text{round}(y)\right) Inew(x,y)=Iold(round(x),round(y))
其中:
- $ I_{\text{new}}(x, y) $ 是目标位置的新像素值。
- $ I_{\text{old}}(x’, y’) $是原始图像中最近邻的已知像素值,其中 $ (x’, y’) $ 由 $ (x, y) $ 四舍五入得到。
2. 双线性插值
双线性插值考虑了目标位置周围的四个最近的已知像素值,并根据其相对位置进行加权平均。对于二维图像上的插值,双线性插值的公式为:
I new ( x , y ) = ( 1 − α ) ( 1 − β ) I old ( x 1 , y 1 ) + α ( 1 − β ) I old ( x 2 , y 1 ) + ( 1 − α ) β I old ( x 1 , y 2 ) + α β I old ( x 2 , y 2 ) I_{\text{new}}(x, y) = (1 - \alpha)(1 - \beta)I_{\text{old}}(x_1, y_1) + \alpha(1 - \beta)I_{\text{old}}(x_2, y_1) + (1 - \alpha)\beta I_{\text{old}}(x_1, y_2) + \alpha \beta I_{\text{old}}(x_2, y_2) Inew(x,y)=(1−α)(1−β)Iold(x1,y1)+α(1−β)Iold(x2,y1)+(1−α)βIold(x1,y2)+αβIold(x2,y2)
其中:
- $ I_{\text{new}}(x, y) $ 是目标位置的新像素值。
- $ I_{\text{old}}(x_i, y_i)$是原始图像中四个最近邻的已知像素值,其中 $ (x_i, y_i) $ 是目标位置的四个相邻像素的坐标。
- $ \alpha = x - x_1 $ 和 $ \beta = y - y_1$。
双线性插值算法涉及到目标位置周围的四个最近邻的已知像素值。这四个最近邻的像素可以通过目标位置坐标的整数部分和小数部分来确定。假设目标位置的坐标为 ((x, y)),则这四个最近邻的坐标可以表示为 ((x_1, y_1), (x_2, y_1), (x_1, y_2), (x_2, y_2)),其中:
- x 1 = ⌊ x ⌋ x_1 = \lfloor x \rfloor x1=⌊x⌋ 是 x x x的整数部分;
- x 2 = ⌈ x ⌉ x_2 = \lceil x \rceil x2=⌈x⌉ 是 x x x的整数部分加一;
- y 1 = ⌊ y ⌋ y_1 = \lfloor y \rfloor y1=⌊y⌋ 是 y y y 的整数部分;
- y 2 = ⌈ y ⌉ y_2 = \lceil y \rceil y2=⌈y⌉ 是 y y y 的整数部分加一。
这四个最近邻的坐标形成了一个矩形区域,如下图所示:
(x1, y1) ---------- (x2, y1)| || || |
(x1, y2) ---------- (x2, y2)
3. 立方卷积插值
立方卷积插值考虑了目标位置周围的八个最近的已知像素值,并使用立方卷积核进行加权平均。对于二维图像上的插值,立方卷积插值的公式较为复杂,其中涉及到立方卷积核的权重计算。
I new ( x , y ) = ∑ i = − 1 2 ∑ j = − 1 2 w ( i , j ) I old ( x + i , y + j ) I_{\text{new}}(x, y) = \sum_{i = -1}^{2} \sum_{j = -1}^{2} w(i, j)I_{\text{old}}(x + i, y + j) Inew(x,y)=i=−1∑2j=−1∑2w(i,j)Iold(x+i,y+j)
其中:
- $ I_{\text{new}}(x, y) $ 是目标位置的新像素值。
- $I_{\text{old}}(x + i, y + j) $ 是原始图像中八个最近邻的已知像素值,其中 $i $ 和 $j $取值为 -1, 0, 1, 2。
- $ w(i, j) $ 是立方卷积核的权重,通常采用一些特定的卷积核形式,如 Bicubic 插值。
在立方卷积插值中,涉及到的是8个点。以下是正确的描述:
对于立方卷积插值,考虑目标位置 ( x , y ) (x, y) (x,y) 周围的8个最近邻点,其坐标可以表示为 ( x i , y j ) (x_i, y_j) (xi,yj),其中:
x i = x − 1 , 0 , 1 , 2 x_i = x - 1, 0, 1, 2 xi=x−1,0,1,2
y j = y − 1 , 0 , 1 , 2 y_j = y - 1, 0, 1, 2 yj=y−1,0,1,2
这样,可以得到一个包含8个点的矩阵,如下所示:
(x-1, y-1) | (x, y-1) | (x+1, y-1) | (x+2, y-1)
(x-1, y) | (x, y) | (x+1, y) | (x+2, y)
(x-1, y+1) | (x, y+1) | (x+1, y+1) | (x+2, y+1)
(x-1, y+2) | (x, y+2) | (x+1, y+2) | (x+2, y+2)
这里的坐标形成了一个4x4的矩阵,但在立方卷积插值中,只需要考虑中间的8个点。这8个点的坐标将用于计算插值权重。
二、 实验代码与现象图
1. 最近邻插值
void CImageProcessingView::OnGeoResizing()
{// 实验 图像缩放//MessageBox("请在这里添加图像缩放的代码");// 获得当前文档对象
CImageProcessingDoc* pDoc = GetDocument();// 判断图像是否已被加载if( pDoc->m_pDibInit->IsEmpty() ){MessageBox("图像未加载");return;}int width = pDoc->m_pDibInit->GetWidth();int height = pDoc->m_pDibInit->GetHeight();int bitCount = pDoc->m_pDibInit->GetBitCount();// 将 m_pDibInit 拷贝至 m_pDibTestpDoc->m_pDibTest->CloneDib(pDoc->m_pDibInit);// 考虑将图像放大两倍的情况 float nResizing = 2;// 获得新的图像高度int newWidth = width*nResizing;int newHeight = height*nResizing;pDoc->m_pDibTest->SetWidthHeight(newWidth, newHeight);//*****************************图像的插值1最近邻插值算法************//int i=0;int j=0;float src_x, src_y;RGBQUAD Quad1;for(i=0;i<newWidth;i++)for(j=0;j<newHeight;j++){src_x = (i / nResizing) + 0.5; //四舍五入src_y = (j / nResizing) + 0.5;Quad1=pDoc->m_pDibInit->GetPixelColor(src_x,src_y);pDoc->m_pDibTest->SetPixelColor(i,j,&Quad1);}// 交换 m_pDibInit 与 m_pDibTest 指针CDib* pTmp = pDoc->m_pDibInit;pDoc->m_pDibInit = pDoc->m_pDibTest;pDoc->m_pDibTest = pTmp; // 设置脏标记pDoc->SetModifiedFlag(TRUE);// 更新视图pDoc->UpdateAllViews(NULL);
}实验现象.
图像放大2倍
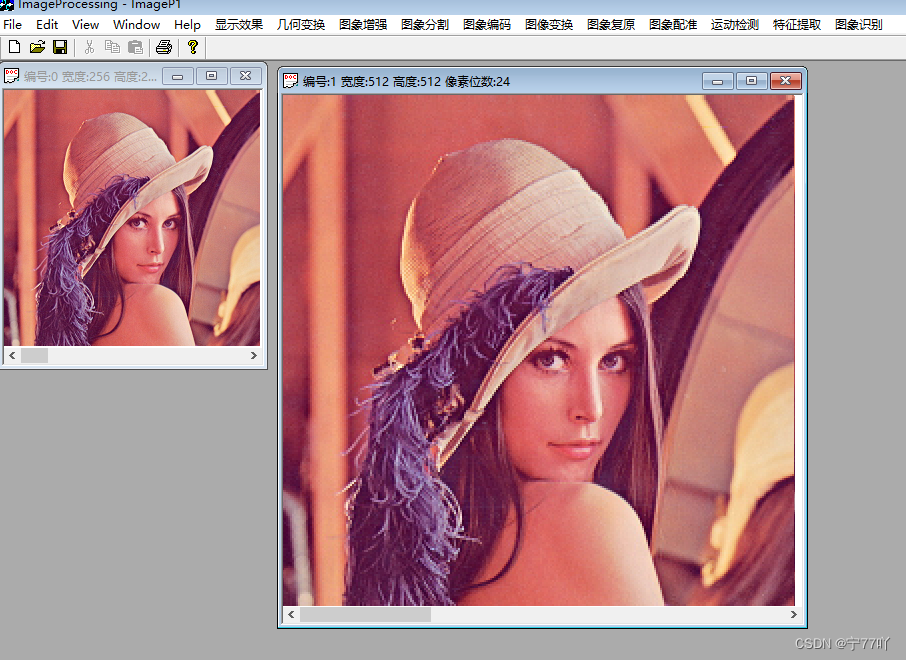
2. 双线性插值
int i=0;int j=0;for(i=0;i<newWidth;i++)for(j=0;j<newHeight;j++){int x=i/nResizing, y = j / nResizing; //定位,找周围四个点float u = i / nResizing,v = j / nResizing; //注意这个类型u =u - x; //所占权重系数v =v - y;int gray0 , gray1 , gray2 , gray3 , GRAY ;gray0 = pDoc->m_pDibInit->GetPixelGray(x, y);//边界处理 非补零if (x + 1 < 256)gray1 = pDoc->m_pDibInit->GetPixelGray(x+1, y);elsegray1 = pDoc->m_pDibInit->GetPixelGray(x, y);if (y + 1 < 256)gray2 = pDoc->m_pDibInit->GetPixelGray(x, y + 1);elsegray2 = pDoc->m_pDibInit->GetPixelGray(x, y);if (x + 1 < 256 && y + 1 < 256)gray3 = pDoc->m_pDibInit->GetPixelGray(x + 1, y + 1);elsegray3 = pDoc->m_pDibInit->GetPixelGray(x, y);GRAY = (1 - u) * (1 - v) * gray0 + (1 - u) * v * gray2 + u * (1 - v) * gray1 + u * v * gray3;pDoc->m_pDibTest->SetPixelGray(i, j, GRAY);}// 交换 m_pDibInit 与 m_pDibTest 指针CDib* pTmp = pDoc->m_pDibInit;pDoc->m_pDibInit = pDoc->m_pDibTest;pDoc->m_pDibTest = pTmp;
实验效果图.
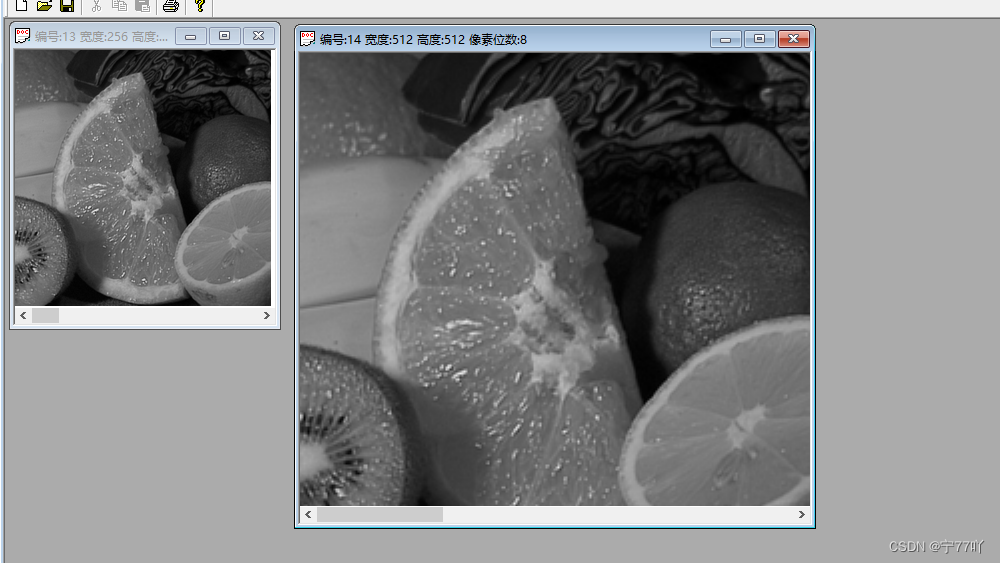
3.立方卷积插值
int a = -0.5; //系数for(int i=0;i<newWidth;i++)for (int j = 0; j < newHeight; j++){int x[4] = { 0 }, y[4] = { 0 };x[1] = i / nResizing, y[1] = j / nResizing; //找点,(1,1)位置x[0] = x[1] - 1; y[0] = y[1] - 1;x[2] = x[1] + 1; y[2] = y[1] + 1;x[3] = x[1] + 2; y[3] = y[1] + 2;float u = (i) / nResizing, v = (j) / nResizing;u =u - x[1]; //所占权重系数(大于0小于1)v =v - y[1];int gray[4][4] = { 0 };float w_x[4] = { 0 }, w_y[4] = { 0 };w_x[0] = 1 + u; w_x[1] = u; w_x[2] = 1 - u; w_x[3] = 2 - u;w_y[0] = 1 + v; w_y[1] = v; w_y[2] = 1 - v; w_y[3] = 2 - v;float W_x[4] = { 0 }, W_y[4] = { 0 };for (int k = 0; k < 4; k++) //计算x和y的权重{if (w_x[k] <= 1 && w_x[k] >= -1)W_x[k] = (a + 2) * pow(w_x[k], 3) - (a + 3) * pow(w_x[k], 2) + 1;else if (w_x[k] > 1 && w_x[k] < 2) W_x[k] = a * pow(w_x[k], 3) - 5 * a * pow(w_x[k], 2) + 8 * a * w_x[k] - 4 * a;elseW_x[k] = 0;if (w_y[k] <= 1 && w_y[k] >= -1)W_y[k] = (a + 2) * pow(w_y[k], 3) - (a + 3) * pow(w_y[k], 2) + 1;else if (w_y[k] > 1 && w_y[k] < 2)W_y[k] = a * pow(w_y[k], 3) - 5 * a * pow(w_y[k], 2) + 8 * a * w_y[k] - 4 * a;elseW_y[k] = 0;}for(int k=0;k<4;k++)for (int m = 0; m < 4; m++){if (x[k] > 0 && x[k]<height && y[m] > 0 && y[m] < width) //判断边界gray[k][m] = pDoc->m_pDibInit->GetPixelGray(x[k], y[m]);elsegray[k][m] = 0;}int Pix_gray = 0; //最终计算得到的灰度值for(int k=0;k<4;k++)for (int m = 0; m < 4; m++){Pix_gray += gray[k][m] * W_x[k] * W_y[m];}pDoc->m_pDibTest->SetPixelGray(i, j, Pix_gray);}
实验效果图.
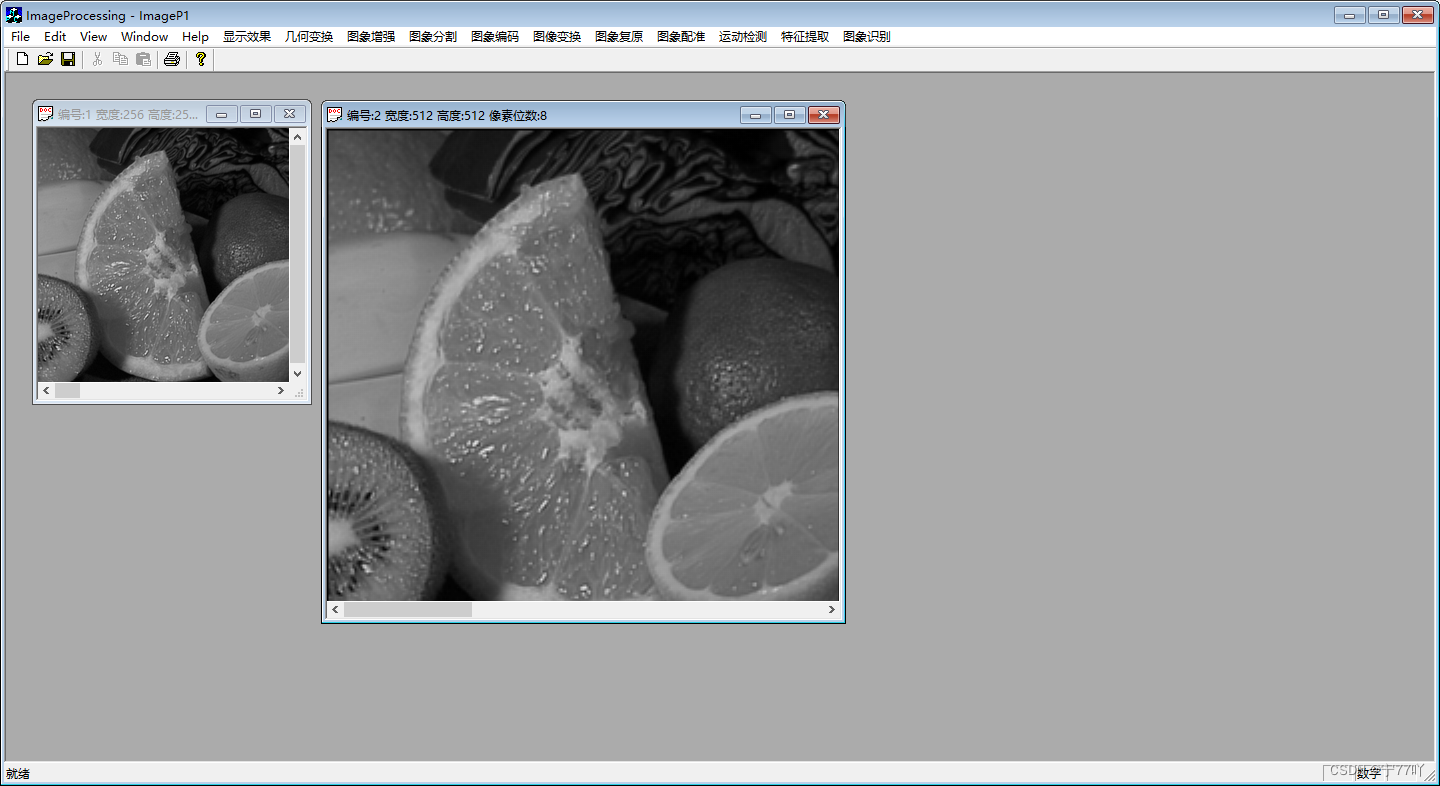
真题解析)

)

)
)



)



)




保存至csv中)
