1. 引言

  深度优先搜索（DFS）是图算法中的一种重要的遍历方法，它通过深度遍历图的顶点来构建生成树。生成树是一个无回路的连通子图，包含了原图的所有顶点，但是边数最少。

本实验将通过C语言实现深度优先搜索生成树。

2. 深度优先搜索生成树

  深度优先搜索是一种递归的图遍历算法，其主要思想是从起始顶点开始，尽可能深入图中的每一个分支，直到不能再深入为止，然后回溯到上一个分支。

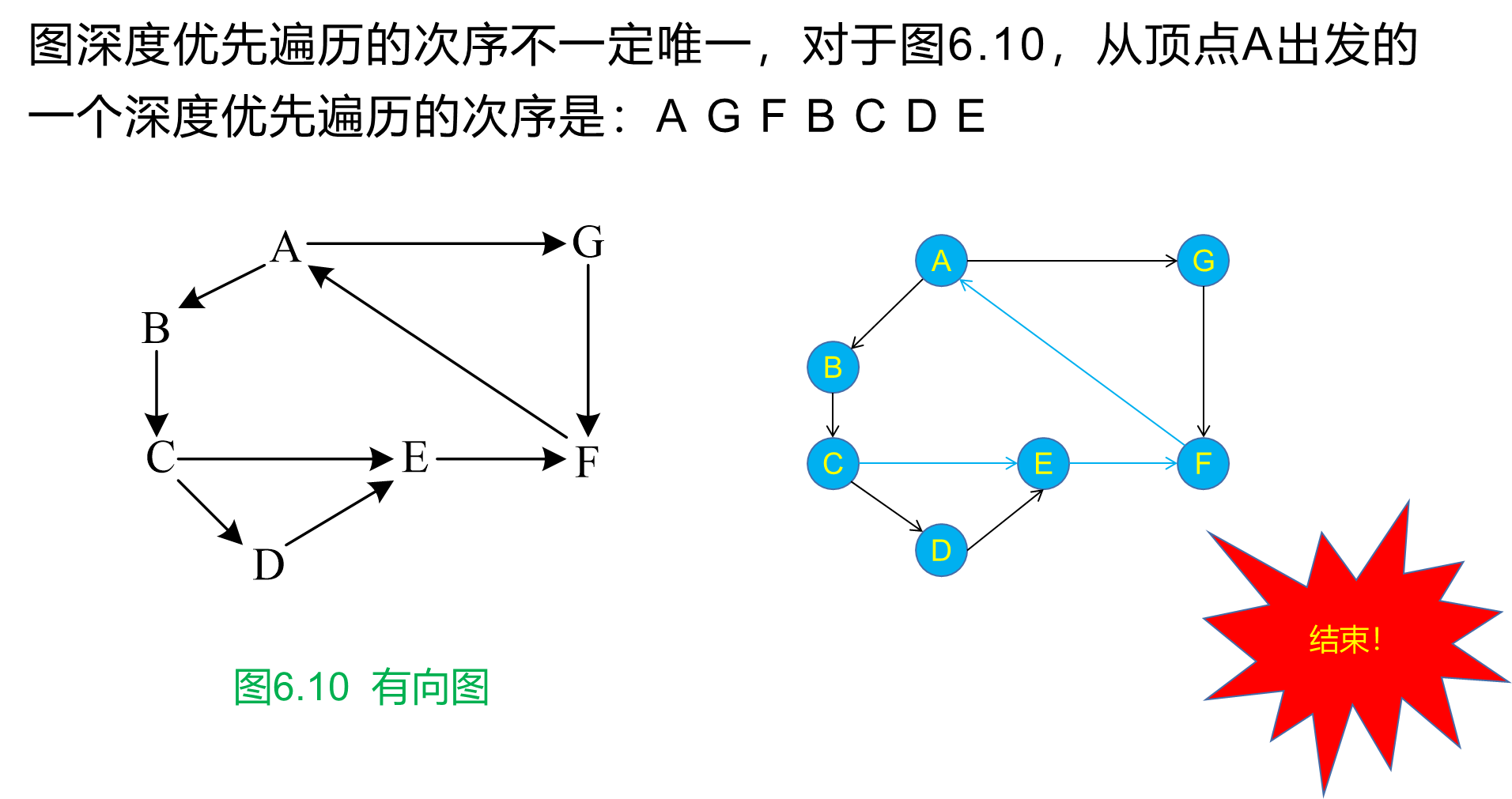
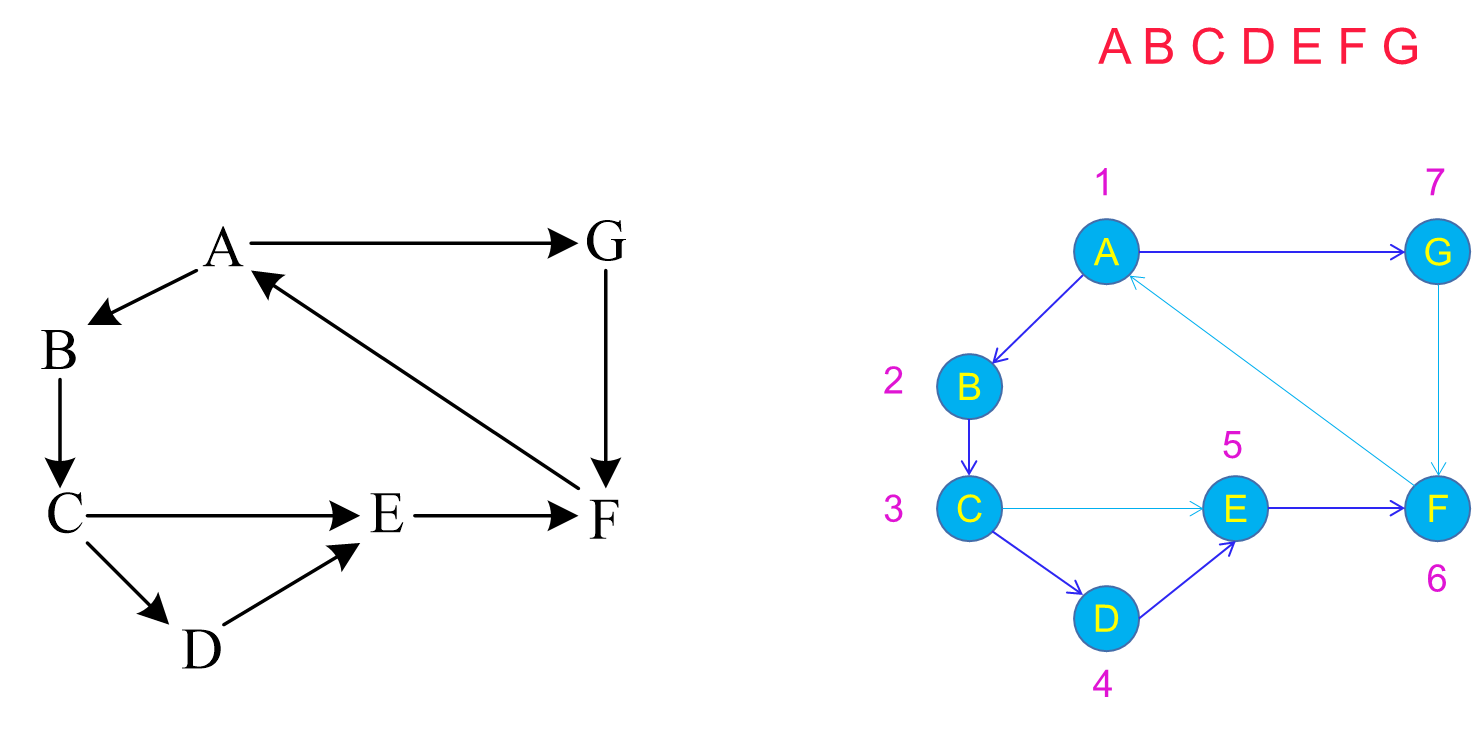
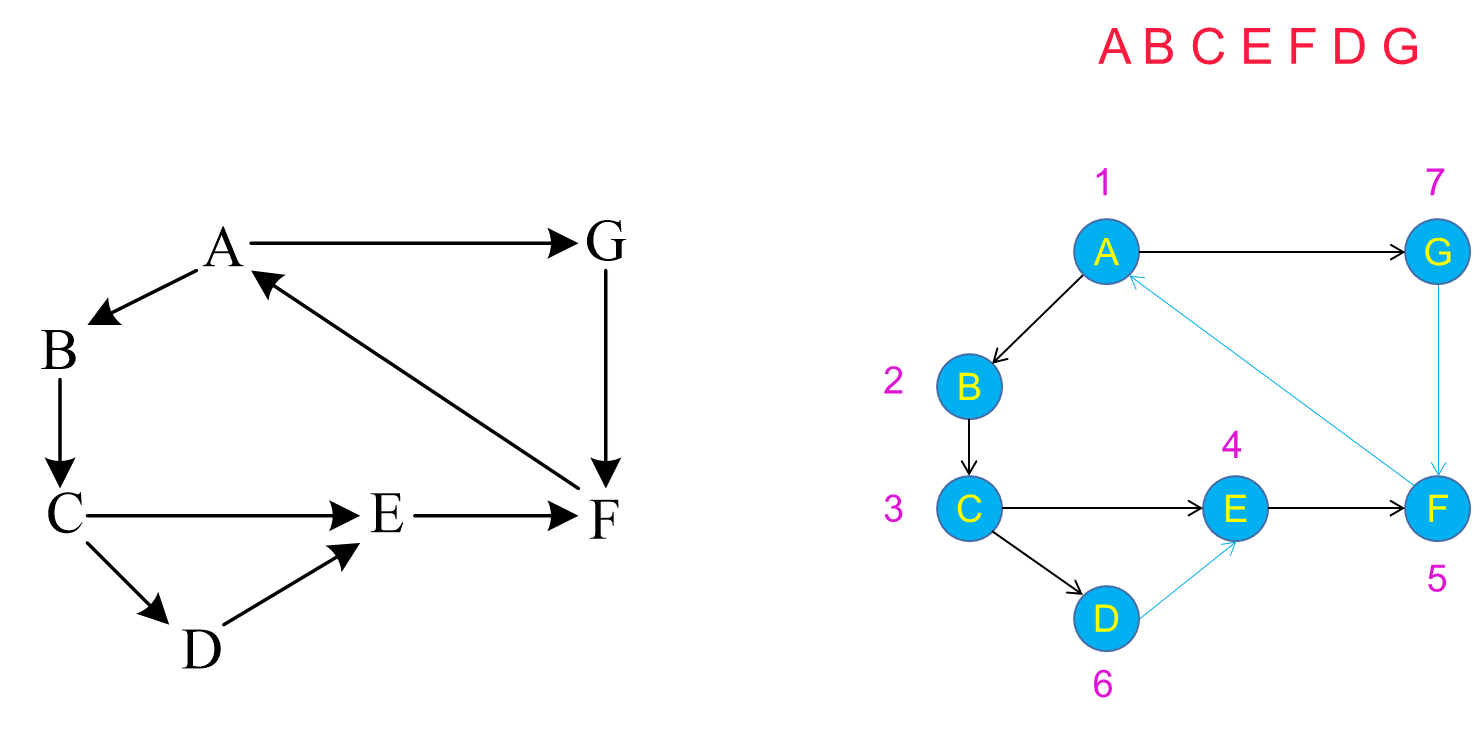
3. 实验内容

3.1 实验题目

   以顶点 0 为起始顶点，求图 G 的深度优先搜索生成树（即深度优先遍历过程形成的树）。

（一）输入要求

{0,1,1,1,1,0,0},
{0,0,1,1,0,0,0},
{1,0,0,0,0,0,0},
{0,0,1,0,0,0,0},
{0,0,0,0,0,1,1},
{0,0,0,0,0,0,1},
{0,0,0,0,0,0,0}

使用前文得到的邻接表做为输入数据

（二）输出要求

输出树中所有结点。结点输出格式如下：（顶点，顶点的父亲，顶点所在的层数）比如，对下面这棵树，有以下输出。

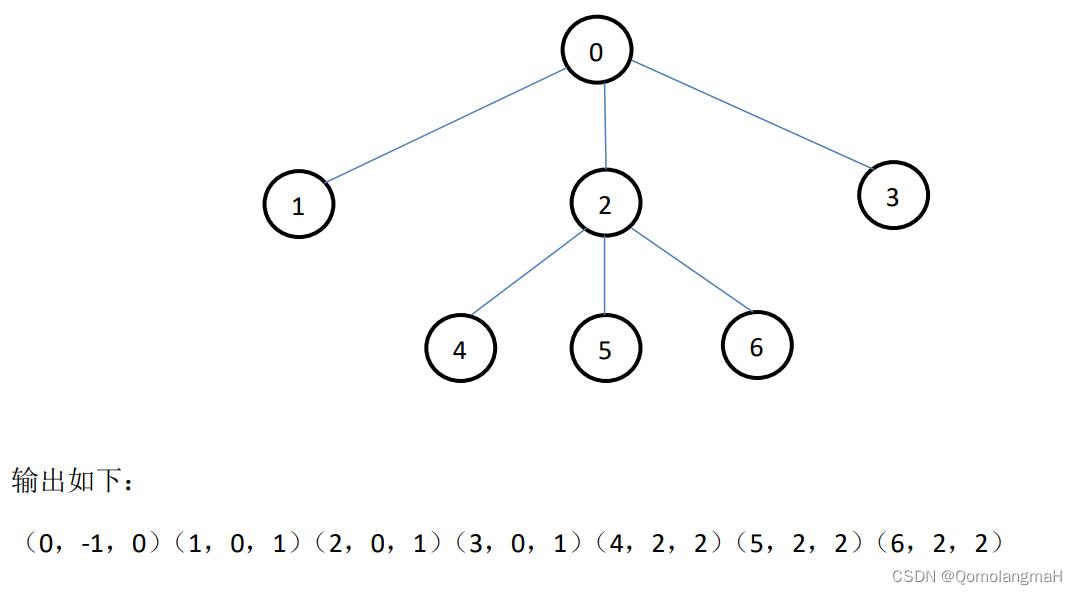
3.2 算法实现

1. 数据结构

typedef struct P {int VerAdj;struct P *link;
} P;typedef struct Q {int VerName;P *Adjacent;int Visited;
} Q;typedef struct {Q Head[20];
} Graph;typedef struct Tree {Q data;struct Tree *FirstChild;struct Tree *NextBrother;
} Tree;typedef struct q {Tree *data;struct q *next;
} Queue;

• P结构体： 用于表示图中的邻接点，VerAdj表示邻接顶点，link指向下一个邻接点。

• Q结构体： 用于表示图中的顶点，VerName表示顶点名称，Adjacent指向邻接点链表，Visited表示是否被访问过。

• Graph结构体： 表示整个图，包含一个数组Head，每个元素表示一个顶点。

• Tree结构体： 表示生成树中的节点，包含一个数据域data，表示顶点，以及FirstChild和NextBrother分别指向第一个孩子和下一个兄弟节点。

• Queue结构体： 用于实现队列，存储生成树的节点。

注：自编代码，比较丑陋，请忽略细节

2. 队列操作函数

void QInsert(Tree *item);
void QDelete();

• QInsert： 将生成树节点插入队列。

• QDelete： 从队列中删除节点。

3. 广度优先搜索遍历

void LevelOrder(Tree *t);

• LevelOrder： 广度优先搜索遍历生成树，输出节点信息，包括顶点、父亲和层数。

4. 创建图

void Create(Graph *g);

• Create： 根据邻接矩阵A创建图，构建邻接表。

5. 深度优先搜索算法

void DepthForceSearch(Graph *g, int i, Tree *t);

• DepthForceSearch： 递归实现深度优先搜索，构建生成树。

6. 主函数及DFS主函数

int main();
void DFS_Main(Graph *g, Tree *t);

• main函数： 创建图，调用DFS_Main进行深度优先搜索，输出生成树的节点信息。

• DFS_Main： 遍历所有未访问的顶点，以每个未访问的顶点为根进行深度优先搜索。

7. 输出生成树信息

void Output(Tree *t);

• Output： 输出生成树的节点信息。

3.3 代码整合

#include <stdio.h>
#include <stdlib.h>#define N 7
int A[N][N] = {{0, 1, 1, 1, 1, 0, 0},{0, 0, 1, 1, 0, 0, 0},{1, 0, 0, 0, 0, 0, 0},{0, 0, 1, 0, 0, 0, 0},{0, 0, 0, 0, 0, 1, 1},{0, 0, 0, 0, 0, 0, 1},{0, 0, 0, 0, 0, 0, 0}
};typedef struct P {int VerAdj;struct P *link;
} P;typedef struct Q {int VerName;P *Adjacent;int Visited;
} Q;typedef struct {Q Head[20];
} Graph;typedef struct Tree {Q data;struct Tree *FirstChild;struct Tree *NextBrother;
} Tree;typedef struct q {Tree *data;struct q *next;
} Queue;Queue *front = NULL, *rear = NULL, *pos = NULL;void QInsert(Tree *item);
void QDelete();
void LevelOrder(Tree *t);
void Create(Graph *g);
void DepthFirstSearch(Graph *g, int i, Tree *t);
void DFS_Main(Graph *g, Tree *t);
void Output(Tree *t);int main() {Graph g;Tree t;Create(&g);printf("深度遍历:\n");DFS_Main(&g, &t);printf("生成树结点信息:\n");Output(&t);return 0;
}void QInsert(Tree *item) {Queue *s = (Queue *)malloc(sizeof(Queue));s->data = item;s->next = NULL;if (front == NULL)front = s;elserear->next = s;rear = s;
}void QDelete() {if (front == NULL) {printf("队列为空");return;}Queue *p = front;front = p->next;free(p);if (front == NULL)rear = NULL;
}void LevelOrder(Tree *t) {if (t != NULL)QInsert(t);while (front != NULL) {Tree *p = front->data;printf("(%d, %d, %d) ", p->data.VerName, t->data.VerName, p->data.VerName);while (p != NULL) {if (p->FirstChild != NULL) {QInsert(p->FirstChild);}p = p->NextBrother;}QDelete();}
}void Create(Graph *g) {int i, j, n, t;for (i = 0; i < N; i++) {g->Head[i].VerName = i;g->Head[i].Adjacent = NULL;P *p = (P *)malloc(sizeof(P));t = 0;for (j = 0; j < N; j++) {if (A[i][j]) {if (t == 0) {g->Head[i].Adjacent = p;p->VerAdj = j;p->link = NULL;t = 1;} else {P *q = (P *)malloc(sizeof(P));q->VerAdj = j;q->link = NULL;p->link = q;p = q;}}}}
}void Output(Tree *t) {if (t != NULL)LevelOrder(t);
}void DepthForceSearch(Graph *g, int i, Tree *t) {P *p;g->Head[i].Visited = 1;p = g->Head[i].Adjacent;t->data = g->Head[i];while (p != NULL) {if (!g->Head[p->VerAdj].Visited) {Tree *child = (Tree *)malloc(sizeof(Tree));child->NextBrother = NULL;child->FirstChild = NULL;DepthForceSearch(g, p->VerAdj, child);Tree *temp = t->FirstChild;if (temp == NULL) {t->FirstChild = child;} else {while (temp->NextBrother != NULL) {temp = temp->NextBrother;}temp->NextBrother = child;}}p = p->link;}
}void DFS_Main(Graph *g, Tree *t) {int i;for (i = 0; i < N; i++)g->Head[i].Visited = 0;for (i = 0; i < N; i++) {if (!g->Head[i].Visited) {Tree *root = (Tree *)malloc(sizeof(Tree));root->NextBrother = NULL;root->FirstChild = NULL;DepthForceSearch(g, i, root);*t = *root;}}
}

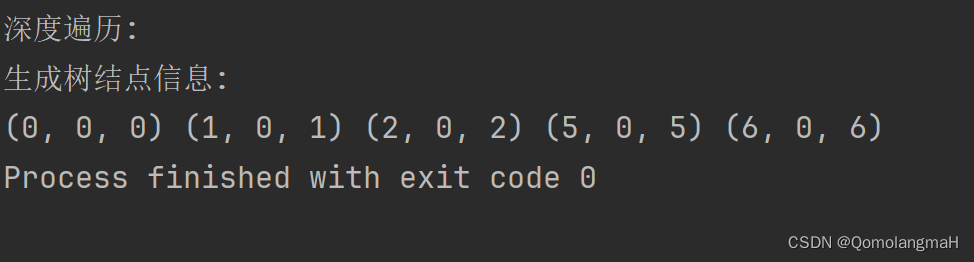
4. 实验结果