【每日一题】二叉树中的伪回文路径

文章目录

Tag
题目来源
题目解读
解题思路
- 方法一：递归（DFS）
- 方法二：位运算
写在最后

Tag

【递归/DFS】【伪回文】【二叉树】【2023-11-25】

题目来源

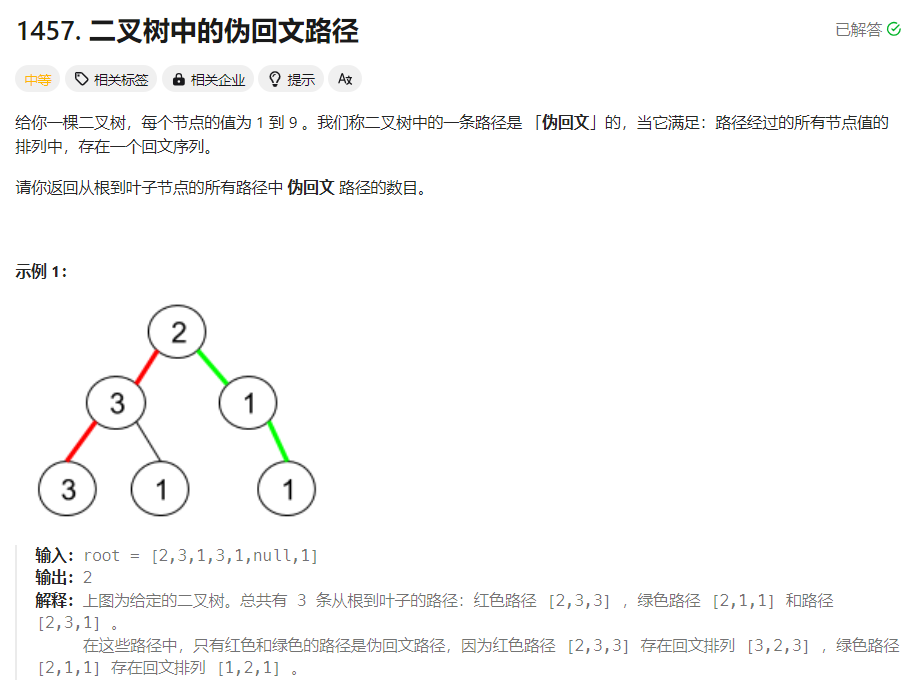
1457. 二叉树中的伪回文路径

题目解读

伪回文路径指的是路径中的节点值经过重新排序之后可以形成回文数的路径。现在需要返回二叉树中所有从根节点到叶子节点的路径中伪回文路径的数目。

解题思路

伪回文的判断

首先来看一下伪回文路径的判断，核心是对于路径节点值的是否具有伪回文性，即将这些节点重新排列之后是否可以构成回文数。比如某条路径上的节点值依次为 2 1 1 ，经过重新排列之后可以形成 1 2 1 这样的回文数，这里的定义不是很清楚，请继续看下去，后面你就会发现其实本题中不需要细究是回文数还是回文串。以下暂且使用回文数来对这样的回文形式进行表达。

回文数分为偶数回文和奇数回文，偶数回文指的是回文数中的字符数量是偶数，根据回文的特性（从左往右与从右往左读到的数都是一致的），回文数中每个字符出现的数量都要是偶数。

奇数回文指的是回文数中的字符数量是奇数，根据回文的特性（从左往右与从右往左读到的数都是一致的），回文数中仅有一个字符出现的数量是奇数（放置在回文数的中心位置），其余字符的出现次数都是偶数。

综上，要判断一个路径节点是否是伪回文的，只需要统计节点中字符个数为奇数的数量 cnt，如果 cnt <= 0，那么就是伪回文的，否则不是。

超出空间限制

本题，最先想到的就是深搜，得到所有可能的数字路径，比如示例 1 中的所有路径为 {{2，3，3}，{2，3，1}，{2，1，1}}，然后遍历统计每一个的 vector 中元素的个数，仅有一个或者零个元素个数是奇数，那么这个 vector就是伪回文的。但是，超出空间限制，关于空间限制，有个疑问，
LeetCode空间限制的思考欢迎讨论。

方法一：递归（DFS）

在深搜的过程中记录这条路径中不同节点出现的次数，在遇到叶子节点时统计：

如果奇数个节点值的个数 cnt <= 1，则该路径是伪回文的；
否则不是。

具体地，使用一个哈希表 mp 来维护出现的节点的数量，设当前节点为 node，更新 ++mp[node->val]：

如果当前节点是叶子节点则调用 chek 函数来更新答案 ans；
否则，递归计算左、右子树；
注意需要回溯的过程，即更新 --mp[node->val]。

实现代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private:int ans = 0;
public:void dfs(TreeNode* root, unordered_map<int, int>& mp){if(!root){return;}++ mp[root->val];if(!root->left && !root->right){// 检查当前的路径是否是 伪回文，并更新答案check(mp);}dfs(root->left, mp);dfs(root->right, mp);-- mp[root->val];}void check(unordered_map<int, int>& mp){int cnt = 0;for(auto [_, freq] : mp){if(freq & 1){++ cnt;}}if (cnt <= 1) {++ ans;}}int pseudoPalindromicPaths (TreeNode* root) {unordered_map<int, int> mp;dfs(root, mp);return ans;}
};

复杂度分析

时间复杂度： $\times n)$ ，其中 $C$ 是节点中不同元素的数量， $n$ 是二叉树中节点数。二叉树中每个元素都会被访问到，每次访问的叶子节点判断是否为伪回文路径的时间复杂度为 $O (C)$ 。

空间复杂度： $O (n)$ ，深搜深度最深为 $O (n)$ 。

方法二：位运算

我们可以使用二进制数来标记路径中的节点出现的数量，节点最多有 10 种，即从 0 到 9，如果某个节点值出现次数为偶数则对应位 1 << (node->val) 记为 0，如果某个节点值出现次数为奇数则对应位 1 << (node->val) 记为 1。我们使用 mask 来表示某条路径中节点出现次数的奇偶数情况，比如 100000011 表示节点值 0、1 和 9 出现次数均为奇数。当前节点 node 的 mask 更新为 mask ^= 1 << node->val。

如果 mask 中只有一个 1 或者没有 1，那么去掉 1 之后，mask 就变成 0 了，那么判断

$KaTeX parse error: Expected 'EOF', got '&' at position 6: mask&̲(mask-1)=0$

是否成立，如果成立则说明 mask 中要么只有一个 1，要么全为 0。

实现代码

代码来源一步步优化：从数组到位运算（Python/Java/C++/Go/JS/Rust）。

class Solution {
public:int pseudoPalindromicPaths(TreeNode *root, int mask = 0) {if (root == nullptr) {return 0;}mask ^= 1 << root->val; // 修改 root->val 出现次数的奇偶性if (root->left == root->right) { // root 是叶子节点return (mask & (mask - 1)) == 0;}return pseudoPalindromicPaths(root->left, mask) +pseudoPalindromicPaths(root->right, mask);}
};