为什么会有并查集

这里可以使用生活中的一个例子来带着大家理解并查集，大家在上学的过程中肯定会发现一种现象，在开学之前大家谁也不认识谁每个人都是一个小团体，可是开学之后因为座位旁边有一个同桌，所以开学没多久你和同桌就会互相认识并且开心的玩在一起，那么这时就是两个一个人的小团体融合成为了一个两个人的小团体，后来你可能会经常把头朝向后面看从而认识了你后面的人，经过了解之后你又跟你后桌的人相互认识从而带着你的同桌和他们玩在一起，那么这个时候两个两人的小团体就会融合成为一个4人的小团体，随着时间的流逝，不同人数的团体相互融合，最终一个班级的人从每个人都是一个小团体变成了一个所有人在一起成为一个大团体，那么为了描述不同团体进行融合的过程就有了查并集这个数据结构。

并查集的原理

我们先来看看并查集的比较官方的定义：在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-findset)。并查集是一个森林，所谓的森林就是指由多个树组成，比如说某公司今年校招全国总共招生10人，西安招4人，成都招3人，武汉招3人，10个人来自不同的学校，起先互不相识，每个学生都是一个独立的小团体，现给这些学生进行编号：{0, 1, 2, 3,4, 5, 6, 7, 8, 9}; 给以下数组用来存储该小集体，数组中数字的绝对值代表：该小集体中具有成员的个数，那么这个数组就如下：

毕业后学生们要去公司上班，每个地方的学生自发组织成小分队一起上路，那么这个时候他们由一个人一个团体合并成为多个人一个团体，于是西安学生小分队s1={0,6,7,8}，成都学生小分队s2={1,4,9}，武汉学生小分队s3={2,3,5}，10个人形成了三个小团体。假设右三个0,1,2担任队长，那么当前的结构就应该变成下面这样：

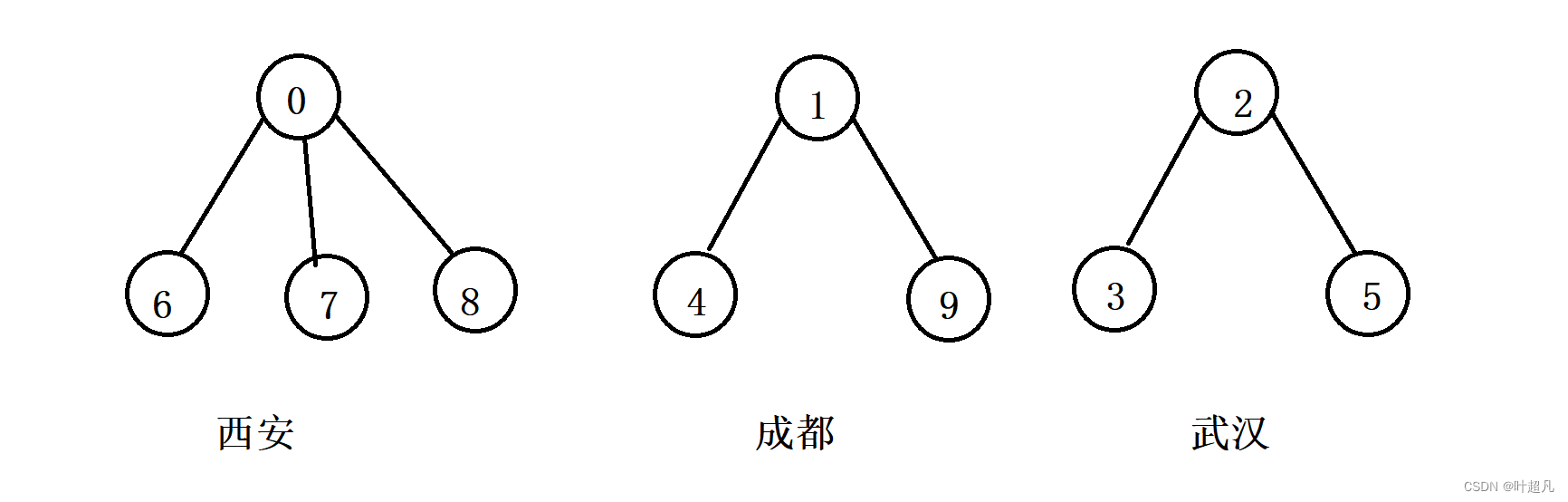
三个团体就是三个树，这三个树再构成一个森林，那么这里就有个问题我们如何把这三个树组合成为一个森林呢？答案是使用数组来对这些树进行合并，数组的下标对应着元素，下标对应的值就表示着不同元素之间的关系，如果你是根节点那么你下标对应的值就表示你这个树里面的节点个数，如果你是子树根节点或者子节点的话，那么你下标对应的值就是你父节点在数组中所在的位置，比如说元素0是西安这个树的根节点，元素0对应在数组中的下标为0，那么下标0中记录的数据就为-4表示西安这个树里面有4个节点，再比如说元素5对应的下标是5，那么在数组中下标5里面记录的数据就是2，表示当前的节点为子节点该节点的父节点在数组中的位置为5，那么其他节点也是依次类推，所以上面的数组就会变成下面这个样子：

知道了如何表示多棵树之后我们就来看看如何将两个树合并成为一棵树，比如说将上面的西安和成都进行合并那么我们就可以通过修改成都树中根节点的父节点，让其指向西安树的根节点来实现，那么这里的图片就变成下面这样：

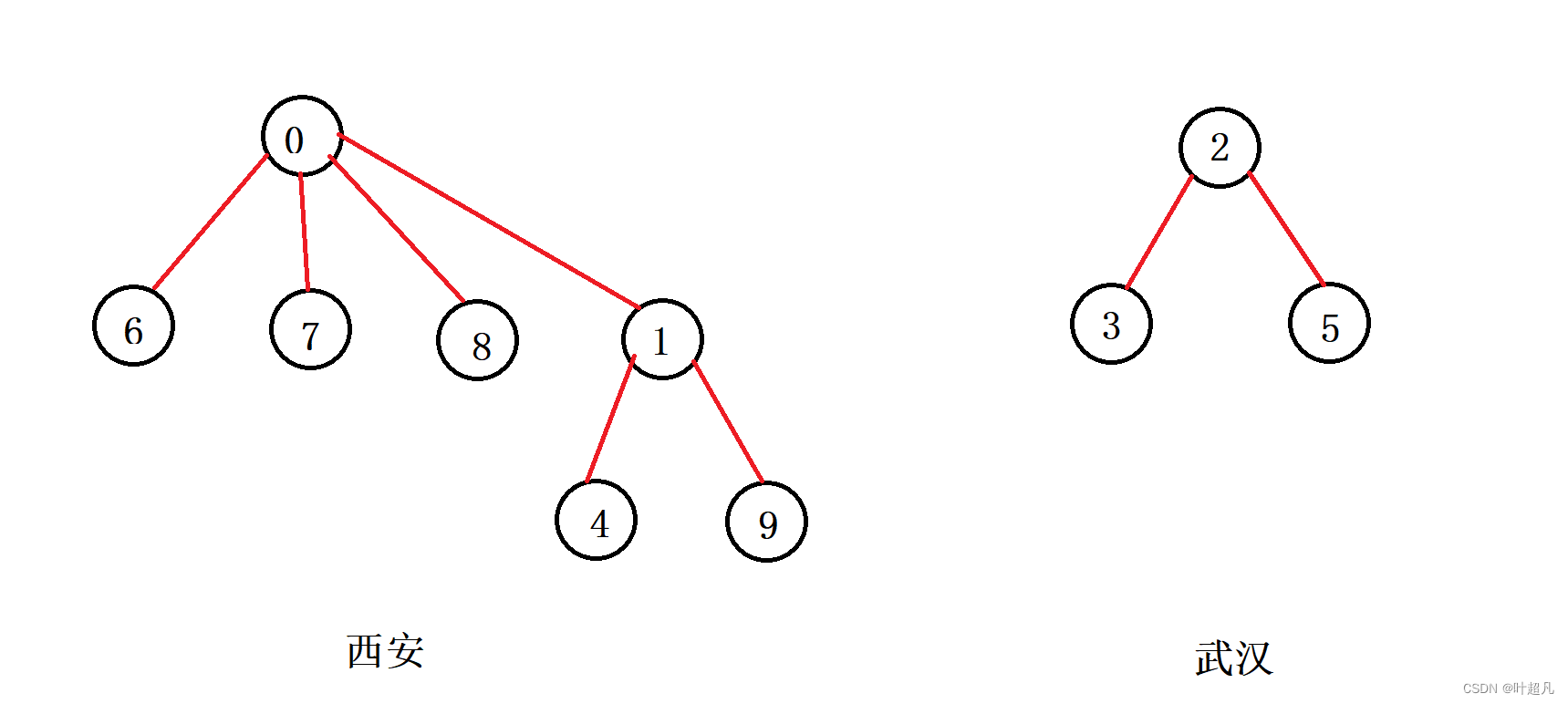
然后在数组中我们就得修改两个树的根节点所对应下标的值，首先将下标为1的值修改成为0表示节点1的父节点为0，将下标为0的值修改成为-7因为融合了一个新的树所以当前树中节点的个数就变多了，那么当前吧数组中的内容就变成下面这样，红色背景表示不同树的根节点，红色从原来的3个变成了2个，那么这就说名当前的森林只有两个树

知道了森林的表示方法和树融合的原理之后我们就可以来模拟实现并查集。

模拟实现并查集

准备工作

首先类里面得存在一个整型数组用来表示每个元素之间的关系：

class UnionFindSet
{
public:private:vector<int> _ufs;//用来表示元素之间的关系
};

但是这样做就会存在一个问题：我们怎么知道数组中的下标对应的是哪个元素呢？所以我们还得创建一个vector容器来方便我们查找下标所对应的元素，又因为元素可以是各种类型所以这里我们得添加一个类模板，模板中存在一个参数表示当前并查集处理的是哪种类型数据的关系，有了这个容器之后我们可以查看下标所对应的元素，那如果我们想查看元素对应的下标又该如何解决呢？所以我们还得创建一个map容器来记录每个元素所对应的下标，那么当前的代码就成为了下面这样：

template<class T>
class UnionFindSet
{
public:private:vector<int> _ufs;//用来表示元素之间的关系vector<T> _a;//根据下标找元素map<pair<T, int>> _indexmap;//根据元素找到下标
};

构造函数

构造函数需要两个参数，一个参数接收当前容器需要处理的数据数组，另外一个参数表示当前处理的数据个数：

UnionFindSet(const T* sorce, size_t num)
{}

然后我们就创建一个循环，在循环里面分别取参数数组的值将其插入到数组_a里面，因为循环是从0开始并且数组_a也是从下标为0的位置开始插入，所以在循环里面我们可以顺便往_indexmap容器种插入数据，那么这里的代码就如下：

UnionFindSet(const T* sorce, size_t num)
{for (size_t i = 0; i < num; i++){_a.push_back(sorce[i]);_indexmap[sorce[i]] = i;}
}

最后将容器_ufs的长度扩容到num，并将每个元素的值都初始化为-1，那么完整的代码就如下：

UnionFindSet(const T* sorce, size_t num):_ufs(num,-1)
{for (size_t i = 0; i < num; i++){_a.push_back(sorce[i]);_indexmap[sorce[i]] = i;}
}

我们可以使用下面的代码来进行以下测试：

int main()
{string s1[] = { "张三","李四","王五","赵六" };UnionFindSet<string> uf(s1, 4);return 0;
}

通过调试我们便可以看到这个容器里面的内容如下：

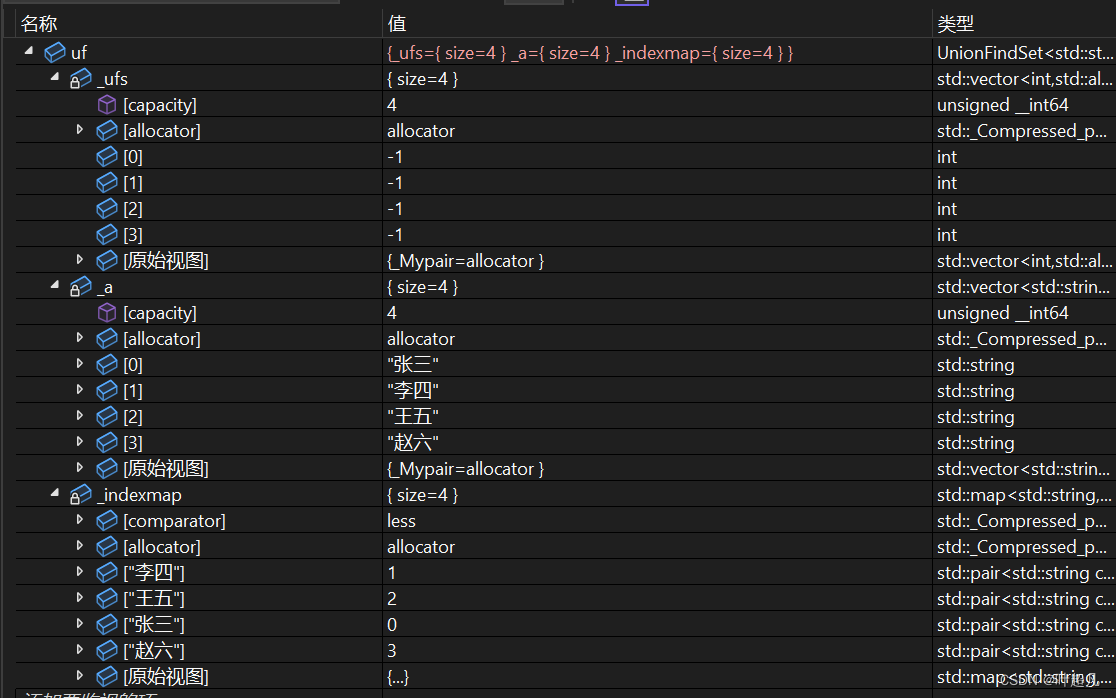
因为我们没有做出任何的合并操作所以ufs数组里面每个元素的值都是-1，_a数组里面记录的是下标所对应的元素，0对应的是张三，1对应的是李四，2对应的是王五，3对应的是赵六，然后_indexmap里面就记录的是元素对应的下标，经过仔细的对比可以看到里面记录的内容和数组中的内容相对应，那么我们的构造函数就实现完成了，接下来来看查找函数。

FindRoot

FindRoot函数就查找一个元素的根节点，如果一个节点不为根节点那么在数组里面它存储的就是它的父节点的下标，如果一个节点为根节点那么它存储的就是当前树种含有节点的个数的赋值，所以在函数里面我们可以创建一个while循环在循环里面一直提取数组中记录的下标，直到下标对应的值为负数位置，那么这里的代码就如下：

size_t FindRoot(T tmp)
{int x = _indexmap.find(tmp)->second;while (_ufs[x] >= 0){x = _ufs[x];}return x;
}

Union

传递两个元素给Union函数，那么该函数就能将两个元素所在的树进行合并，在函数的开始我们先判断一下这两个元素所在树的根节点是否相同，如果相同如果不相同的话我们就进行合并，那么这里的代码就如下：

void Union(T tmp1, T tmp2)
{size_t x1 = FindRoot(tmp1);size_t x2 = FindRoot(tmp2);if (x1 != x2){//根节点不相等才进行合并}
}

合并的过程很简单将某个根节点的值加到另外一个根节点上，然后将值更改成为另外一个根节点的下标即可，那么这里的代码就如下：

void Union(T tmp1, T tmp2)
{size_t x1 = FindRoot(tmp1);size_t x2 = FindRoot(tmp2);if (x1 != x2){//根节点不相等才进行合并_ufs[x1] += _ufs[x2];_ufs[x2] = x1;}
}

SetCount

这个函数的功能就是统计当前容器里面存在几棵树，那么这里我们直接通过循环遍历数组_ufs，里面存在几个元素为负数的节点就说明当前容器里面存在几棵树，那么这里的代码就如下：

size_t SetCount()
{size_t num = 0;for (auto ch : _ufs){if (ch < 0){num++;}}return num;
}

并查集实战

题目一：省份数量

题目详细：

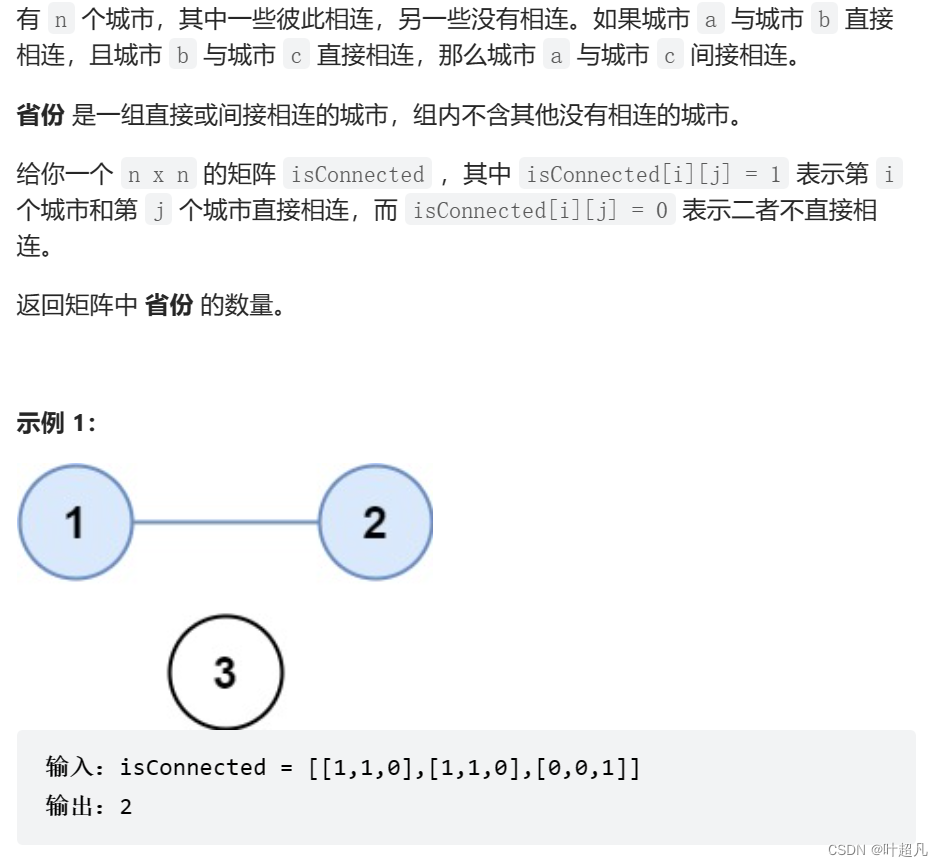
题目链接->点击此处尝试做题

题目解析

有了并查集之后做这种题简直就是小菜一碟，首先题目给了我们一个二维数组，这个数组里面表示各个城市之间的相连接情况，如果isConnected[0][1]等于1，那么这就表示1号城市和2号城市相联通，然后把一群相互联接的城市称为省份，最后题目要求我们根据一个二维数组来判断当前存在多少个省份，那么这里我们就可以先创建一个并查集对象，然后创建一个内嵌for循环判断二维数组中相互链接的城市，如果一个第i号城市和第j号城市相互连接的话就使用并查集对这两个城市进行合并，遍历完成之后就可以返回并查集中的SetCount函数来结束本题，因为题目传递的参数是一个vector<vector<int>>的容器，而我们上面实现的并查集的构造函数需要一个数组，所以为了方便我们对上面的类进行简化，让其专门服务于int类型的数据那么这里的代码如下：

class UnionFindSet
{
public:UnionFindSet(int size): _set(size, -1){}size_t FindRoot(int x){while(_set[x] >= 0)x = _set[x];return x;}void Union(int x1, int x2){int root1 = FindRoot(x1);int root2 = FindRoot(x2);if(root1 != root2){_set[root1] += _set[root2];_set[root2] = root1;}}size_t SetCount(){size_t count = 0;for(size_t i = 0; i < _set.size(); ++i){if(_set[i] < 0)count++;}return count;}private:std::vector<int> _set;
};

然后这道题的代码就如下：

int findCircleNum(vector<vector<int>>& isConnected) {UnionFindSet uf(isConnected.size());for(int i=0;i<isConnected.size();i++){for(int j=0;j<isConnected[0].size();j++){if(i!=j&&isConnected[i][j]==1){uf.Union(i, j);}}}return uf.SetCount();
}

测试的结果如下：

可以看到运行的结果是正确的。

题目二：等式方程的可满足性

题目链接->点击此处尝试做题

题目解析

这道题很明显也是使用并查集进行解决，数组中提供很多表达式，那么我们首先创建一个for循环将表达式中所用相等的元素都合并到一起，然后再创建一个循环判断每个不相等的表达式看两遍的元素是否属于同一个树，如果是树的话就直接返回false，如果不属于同一个树的话就接着往下进行判断，如果所有元素都判断完并且没有出错的话就返回true，题目给的参数形式如下：

bool equationsPossible(vector<string>& equations) {}

我们不知道元素个数，所以这里直接将空间拉到最大一共有26个因为字母，那么这里就开26个大小，然后使用相对映射法进行合并字符a对应的是0，字符b对应的是1这样一直往后，那么这里的代码就如下：

bool equationsPossible(vector<string>& equations) {UnionFindSet uf(26);for(auto ch:equations){if(ch[1]=='='){uf.Union(ch[0]-'a', ch[3]-'a');}}for(auto ch:equations){if(ch[1]=='!'){if(uf.FindRoot(ch[0]-'a')==uf.FindRoot(ch[3]-'a')){return false;}}}return true;}

代码的运行结果如下：

可以看到运行的结果是正常的。